第七章 第一节 功

图示为用细线悬挂的小球在竖直平面内左右摆动的频闪照片。图中的小球自右侧初始位置释放后沿圆周摆至最低点,由于尺子对细线的阻挡,小球继续向左侧摆动,圆周轨道半径减小。我们发现,小球在左右两侧所能到达的最大高度大致相等;小球自高处向低处运动时,相邻影像之间的间隔越来越大。这两个现象背后的物理原理是什么呢?
空气阻力较小时,单摆摆动过程中机械能近似守恒的情境比较容易呈现。此过程也经常被用来代替伽利略的理想斜面实验。可结合必修一中的“斜面实验”引导学生分析两者的共同点,猜想其中的不变量;为机械能守恒定律的学习埋下伏笔。教师也可引导学生用摄像机自行拍摄有关过程,利用适当的辅助手段分析比较摆球在两侧所达到的最大高度。
可引导学生根据章首图以及相关说明文字分析摆球摆动过程中的速率变化,猜想摆球摆动过程中高度与速率的定性关系,为学生提供通过寻求科学证据进行科学猜想的实际经历。
第七章
- 在本章中我们将:
1.理解功、功率、动能、重力势能等概念,理解动能定理,知道重力势能的变化与重
力做功的关系,定性了解弹性势能,理解机械能守恒定律。
2.根据牛顿定律推导动能定理,通过实验验证机械能守恒定律。
3.运用动能定理、机械能守恒定律分析、解释生产生活中的有关问题和现象。
- 本章的学习将用到物体的匀变速直线运动、曲线运动规律和牛顿定律。
- 本章的学习有助于能量观念和守恒思想的形成,为运用功能关系、守恒定律分析较为复杂的运动过程奠定基础。
学习目标
1.会用动能定理和机械能守恒定律解释简单的现象,解决简单的实际问题,形成用机械能转化和守恒的思想分析问题的意识,初步建立能量观念。
2.能将简单问题中物体的运动过程进行抽象,体会科学抽象的思维方法,能从功和能的角度用简单的证据表达自己的观点;在应用机械能守恒定律解决问题的过程中,体会守恒的思想,领悟用守恒思想分析问题的方法。
3.在验证机械能守恒定律的实验中,经历记录、分析和处理实验数据的过程,能根据证据得出结论并作出解释,能通过相互交流来表达实验的过程和结果。
编写意图
课程标准中对本章内容的要求为:
2.1.1 理解功和功率。了解生产生活中常见机械的功率大小及其意义。
2.1.2 理解动能和动能定理。能用动能定理解释生产生活中的现象。
2.1.3 理解重力势能,知道重力势能的变化与重力做功的关系。定性了解弹性势能。
2.1.4 通过实验,验证机械能守恒定律。理解机械能守恒定律,体会守恒观念对认识物理规律的重要性。能用机械能守恒定律分析生产生活中的有关问题。
在初中学习的基础上,本章要求理解功和能的定量表述,进一步理解功和能的定量关系,在解决相关实际问题的过程中感受动能定理相对于牛顿运动定律的优势,以及运用动能定理和牛顿运动定律解决问题的不同特点。
由动能定理结合势能与保守力做功的关系推出机械能守恒定律,并通过实验验证机械能守恒定律,认识理论推演与实验验证在探究物理规律过程中的作用和意义。在理解牛顿运动定律及初步建立“运动与相互作用”观念的基础上,能描述外力对物体所做的功和物体运动的情况,能用机械能转化和守恒的思想分析问题,能用动能定理和机械能守恒定律解释生活中简单的现象,解决简单的实际问题。通过机械能守恒定律的应用,经历定量运算,感受机械能守恒定律对解决实际问题的重要意义。
本章内容揭示了运动、相互作用和能量之间的相互关系,帮助学生初步建立能量观念,并初步感受守恒的思想。
完成本章内容的学习,共需要 13 课时。其中,第一节 2 课时,第二节 2 课时,第三节 4 课时,第四节 2 课时,第五节 3 课时。

图 7–1 上海洋山深水港大型吊装机械
本节编写思路
本节从机械提升重物的情境引出功的概念,并在初中已学知识的基础上,理解恒力做功的计算式。
通过问题“力怎样才能做功?”“怎样计算恒力的功?”的递进引领,引出做功的条件、功的计算等内容。
第一部分以物理学史和“自主活动”为依托,理解功的概念和做功的条件。第二部分通过对曲线运动过程中恒力对物体做功的分析,体验用微元法分析问题的思想,并在示例中加以巩固。第三部分用“力–位置”图像表示功,既作为公式的补充,也为变力做功的拓展打下基础。
在学习过程中经历微元法分析的过程,有助于学生科学思维的培养。

图 7–2 《天工开物》中的
桔槔图
马车由静止开始沿水平地面向前做加速运动,是因为马对车做了功。在初中已经学过功的概念以及简单机械的知识。无论是图 7–1 中现代化港口的大型吊装机械,还是图 7–2 中我国古代的提水机械——桔槔,都是通过做功来提升重物的。不仅机械可以做功,所有的物体甚至人体自身都能做功。做功需要力,重力、弹力和摩擦力都能做功。物理学中,把这些力所做的功叫做机械功(mechanical work),简称功。
功的概念起源于第一次工业革命大规模使用的热机,当时为了寻找一种能够比较蒸汽机效益的办法,人们在实践中逐渐认同用“机器举起物体重量与高度的乘积”来量度蒸汽机的效益,并称之为“功”。19 世纪初,科里奥利(G.Coriolis,1792–1843)明确地把作用力和受力点沿作用力方向的位移的乘积叫做“功”。教材图 7–1、图 7–2所示的机械,都被用来提升重物,以此呼应功的早期定义。而本节引言选用马拉车做功,使马车加速,说明功的概念不局限于竖直方向提升重物的过程,做功的效果可以使重物高度增加(重力势能增大),也可以使物体加速(动能增大)。
第一次工业革命时,人们为了比较蒸汽机的效益建立了功的概念。1826 年,法国物理学家科里奥利(G.Coriolis,1792 – 1843)引入“功”一词,并将其定义为用机器“举起物体的重量与高度的乘积”。现在,这一定义已经大为扩展了。
在初中,我们所学的计算功的公式是
\[W = Fs\]

图 7–3 焦耳
(J.Joule,1818—1889)
式中,F 表示物体受到的力的大小,s 是物体在力的方向上通过的距离。现在将 s 定义为物体在力的方向上发生的位移大小,因此,当物体在力的方向上发生位移时,称力对物体做了功。功是标量。在国际单位制中,力的单位是 N,位移的单位是 m,功的单位就是 N·m。为了纪念英国物理学家焦耳(图 7–3),将功的单位命名为“焦耳”,用符号 J 表示,即 1 J = 1 N·m。
图7–4所示分别为举重运动员训练的四种情况:图(a)为缓慢上举过程;图(b)为举着不动;图(c)为缓慢向前移动;图(d)为缓慢下蹲过程。请你说说在这四种情况下运动员都对杠铃做功吗?你认为怎样才能做功?

(a) (b) (c) (d)
图 7–4 举重运动员训练的四种情况
此处设置“自主活动”的目的是引导学生利用初中关于功的基础知识分析图(a)(b)(c)的情况。
参考答案:图(a)做正功,图(b)(c)不做功,图(d)做负功。物体在力的方向上有位移时才能做功。
利用初中所学的功的计算式,我们可以讨论图 7–4(a)、(b)和(c)中运动员对杠铃做功的情况。图 7–4(d)中,杠铃向下移动,而运动员对杠铃的作用力向上。这时,运动员是否对杠铃做功呢?
图 7–5 恒力对物体做功
在一般情况下,作用在物体上的力与物体位移的方向不一定相同,这时可以用矢量分解的方法来分析力做功的情况。
如图 7–5 所示,物体受恒力 F 的作用由 A 沿直线运动到 B,F 与物体位移 s
成 θ 角。这时可以将 F 沿 s 方向和与 s垂直的方向分解成两个分力 F1、F2。其中,F1 与 s 在同一直线上,则 F1 对物体做功。由于 F1 = Fcosθ,故 F1 对物体做功为 W = F1s = Fscosθ。F2 与 s 垂直,物体在 F2 的方向上无位移,故 F 对物体做功为零。
综上所述,物体做直线运动时,恒力对物体所做的功等于恒力大小、位移大小、恒力与位移之间夹角 θ 的余弦三者的乘积,即
由于必修课程内的研究对象仅限于质点,故功的计算式中,s 为质点的位移。在一般情况下,s 应理解为受力点的位移。如图 1 所示,通过弹簧拉静止于水平桌面上的物体,物体虽然不动,但拉力的受力点有移动,拉力仍然做功(弹簧弹性势能增大)。可根据学生的具体情况,结合数学中向量内积的知识,介绍功的计算式的矢量形式 W = F·s,体现学科综合的思想。

\[\color{#357A4A}{W = Fs\cos \theta}\]
能否通过分解位移获得恒力做功的计算式?
此处设置“大家谈”的目的是引导学生通过分解位移的方式得到相同的结论,使学生体验两种方法的等价性,培养学生从不同角度分析问题的意识。
物体做曲线运动时,恒力对物体所做的功怎样计算呢?
如图 7–6(a)所示,物体沿任意曲线路径由 A 运动到 B,作用于物体的恒力 F 与物体位移 s 所成角为 θ。
通过恒力在曲线运动过程中做功的分析,明确恒力做功的计算式对曲线运动也同样适用。同时,提供一个运用微元法分析问题的范例,帮助学生理解“功是力对空间的积累效应”,也为第四节学习重力做功的特点做好铺垫。
教师可视具体情况引导学生进一步分析物体沿任意曲线路径由 B 返回 A 的过程中,恒力 F 所做的功,进而总结物体沿闭合路径运动过程中恒力做的功。以上分析表明,恒力做功具有保守力做功的特点。
所谓恒力,是指其大小和方向均不随空间位置和时间变化的力,而且只决定于施力物体和受力物体之间的相互作用,与受力物体的运动状态(即速度)无关。设恒力为 F,则 F 做的功
\[W = \int_A^B {{\bf{F}} \cdot d{\bf{s}}} = {\bf{F}} \cdot \int_A^B {d{\bf{s}}} = {\bf{F}} \cdot {{\bf{s}}_{AB}}\]
其中,F 为恒力,sAB 为位移。由上式易见,恒力 F 沿闭合路径做功必为零,∮s F·sAB = 0。
如图 7–6(b)所示,将物体途经的曲线路径分割成无限多微小段,物体经过每一微小段的运动可视为直线运动。图 7–6(b)中第 i 个微小段的位移 Δsi 与恒力 F 所成的夹角为 θ,在这段微小位移上,恒力 F 做的微小功 ΔWi = FΔsicosθi。将 Δsi 沿 F 方向和与 F 垂直的方向分解成两个分位移 Δsi1,和 Δs2,Δsi1 = Δsicosθi,Δsi2 = Δsisinθi。因此,ΔWi = FΔsi1。
物体从 A 沿曲线运动到 B 过程中,恒力 F 对物体所做的功 W 就是每一段微小位移上恒力 F 所做功的代数和,即
\[W = \Delta {W_1} + \Delta {W_2} + \cdots = F\Delta {s_{11}} + F\Delta {s_{21}} + \cdots = F(\Delta {s_{11}} + \Delta {s_{21}} + \cdots )\]
从几何角度而言,上式中的(Δs11 + Δs21 + …)即每一微小段位移沿 F 方向分量的累加,其结果等于图 7–6(a)中位移 s 沿 F 方向的分量 s1,s1 = scosθ。
图 7–6 曲线运动中恒力对物体做的功
综上所述,物体做曲线运动时,恒力对物体所做的功也等于恒力大小、位移大小、恒力与位移之间夹角的余弦三者的乘积,即
\[\color{#357A4A}{W = Fs\cos \theta}\]
由此可见,恒力所做的功不仅取决于恒力的大小和位移的大小,还取决于恒力和位移之间的夹角。
当 0 ≤ θ < \(\frac{\pi }{2}\) 时,cosθ > 0,W > 0,称恒力做正功;
当 θ = \(\frac{\pi }{2}\) 时,cosθ = 0,W = 0,称恒力不做功;
当 \(\frac{\pi }{2}\) < θ ≤ π 时,cosθ < 0,W < 0,称恒力做负功,或称物体克服恒力做功。
如图 7–4(d)所示,运动员对杠铃的作用力与杠铃位移的夹角为 π,运动员对杠铃做负功。
实际情况下,物体往往受到多个力的作用,从而需要计算多个力对物体所做的总功。由于功是标量,故无论物体是受多个力先后作用还是受多个力同时作用,所有力对物体所做的总功等于各个力对物体所做功的代数和。若物体可以被视作质点且受多个力同时作用,则所有的力均为共点力,它们所做的功也等于所有力的合力所做的功。
这里的公式 W = Fscosθ 以及多个力做的总功等于合力做的功,均只适用于质点,而一般情况下,多个外力对物体做功的代数和并不一定可以用合外力与位移的内积来计算。这是因为一方面对非质点的情形,如果作用于物体的多个力并非一定是共点力,并不能用合力描述;另一方面各个力的作用点的位移也可能并不一致。例如,作用于弹簧两端的拉力做的功和作用于刚体使之加速旋转的力偶做的功。教师可视具体情况引导学生分析如图 2 所示过程中,作用于轻弹簧两端、等大、反向的恒力 F1 和 F2 将弹簧拉长 x 的过程中所做的总功。
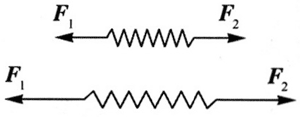
图 7–7 工人推包裹
示例 如图 7–7 所示,工人将重 G = 100 N、装满棉花的包裹沿离地高 h = 1 m的水平平台由静止开始从 A 处推至平台边缘 B 处,A、B 间的距离为 4 m;工人对包裹施加恒定的推力,推力大小 F = 50 N,推力与水平面的夹角 θ = 37°;包裹到达 B 处时,撤去推力,包裹随即在重力作用下落至水平地面上的 C 处。若包裹与平台间的动摩擦因数 μ = 0.2,分别求出作用于包裹的各个力所做的功,以及这些力所做的总功。(忽略空气阻力)
示例选择工人推包裹的实际情境,针对水平直线运动和平抛曲线运动两段过程求解全过程中各个力做功。具体结果涉及正功、负功和不做功各种情况。其中,物体自 B 处经平抛运动落至 C 处的过程中,重力做功的计算呼应了此前对曲线运动中恒力做功特点的分析,亦为第四节重力做功的特点埋下伏笔。
图 7–8 包裹的受力分析
分析:包裹自 A 处被推至 B 处的过程中受四个大小与方向均不变的力作用,包裹由 B 落至 C 的过程中仅受重力作用。因此,只要明确各个力与位移的夹角,即可利用恒力做功的公式计算各力所做的功,这些力所做功的代数和就是它们对包裹所做的总功。
解:以包裹为研究对象,包裹由 A 运动至 B 过程中的受力分析如图 7–8 所示,包裹受到大小与方向均不变的推力 F、平台的支持力 FN、摩擦力 Ff 和重力 G 的作用。
设包裹由 A 至 B 的位移为 s,G、FN、Ff 与 s 的夹角分别为 α、β 和 γ,则 s = 4 m,α = 90°,β = 90°,γ = 180°。
根据竖直方向的力平衡关系可得
\[{F_{\rm{N}}} = G + F\sin \theta = (100 + 50 \times \sin 37^\circ )\;{\rm{N}} = 130\;{\rm{N}}\]
则
\[{F_{\rm{f}}} = \mu {F_{\rm{N}}} = 0.2 \times 130\;{\rm{N}} = 26\;{\rm{N}}\]
由已知条件和恒力做功的计算式可知,包裹由 A 被推至 B 的过程中:
重力做功
\[{W_{\rm{G}}} = Gs\cos \alpha = 100 \times 4 \times \cos 90^\circ {\rm{J}} = 0\]
支持力做功
\[{W_{\rm{N}}} = {F_{\rm{N}}}s\cos \beta = 130 \times 4 \times \cos 90^\circ {\rm{J}} = 0\]
推力做功
\[{W_{\rm{F}}} = Fs\cos \theta = 50 \times 4 \times \cos 37^\circ {\rm{J}} = 160\;{\rm{J}}\]
摩擦力做功
\[{W_{\rm{f}}} = {F_{\rm{f}}}s\cos \gamma = 26 \times 4 \times \cos 180^\circ \;{\rm{J}} = - 104\;{\rm{J}}\]
包裹由 B 落至 C 的过程中,只有重力做功,设包裹的位移为 s′,重力与位移的夹角为 φ,则重力做功
\[{W_{\rm{G}}}^\prime = Gs'\cos \varphi = Gh = 100 \times 1\;{\rm{J}} = 100\;{\rm{J}}\]
整个过程中,包裹受到的作用力所做的总功为
\[W = {W_{\rm{F}}} + {W_{\rm{G}}} + {W_{\rm{N}}} + {W_{\rm{f}}} + {W_{\rm{G}}}^\prime = (160 + 0 + 0 - 104 + 100)\;{\rm{J}} = 156\;{\rm{J}}\]
当力的方向与受力物体的位移沿同一直线时(力与位移的夹角为 0 或 π),力对物体所做的功可以用图像来表示。
图 7–9 所示为恒力与位置的关系图像。图中横坐标 x 表示物体的位置,纵坐标 F 表示力。该图像称为力–位置图像,即 F–x 图。图线下阴影面积表示在一段位移上力做的功。
可通过与 v–t 图面积的物理意义的类比,进一步强化 F–x 曲线与 x 轴所围面积的物理意义。
图 7–9 恒力的力–位置图像
如图 7–10(a)所示,物体从 x = x0 处沿直线运动到 x = xf 处的过程中,力 F 的方向始终和物体的位移方向一致,但其大小随物体的位置 x 变化。
在此情形下,将物体在整个过程中的位移分为无限多微小位移 Δx(Δx → 0)。在每一段 Δx 中,F 的变化很小,视为恒力。对于图中第 i 段微小位移 Δxi,Fi 做的微小功 ΔWi = FiΔxi,即图 7–10 (a)中蓝色窄条矩形的面积。物体从起点运动到终点的过程中,F 对物体做的功为所有微小功的累加,即
\[W = \Delta {W_1} + \Delta {W_2} + \cdots = {F_1}\Delta {x_1} + {F_2}\Delta {x_2} + \cdots \]
从几何角度而言,上述累加表示将图 7–10 (a)中无限多窄条矩形的面积进行累加,其结果正好等于图 7–10 (b)中从起点到终点之间图线下方的面积。
图 7–10 变力的力–位置图像
教师可视具体情况,将 F–x 图面积的物理意义推广至变力做功的情况。建议与变速直线运动中分析 v–t 图面积物理意义的过程类比。教师可提供线性变力做功的示例供学生练习,并介绍对位移的平均力概念。
- 运动员用 100 N 的力将球踢出,球滚出的距离是 10 m。某同学根据 W = Fs 得出运动员踢球做的功是 1 000 J。这种算法是否正确?简述理由。
- 周末,小明在家打扫卫生,他先把沙发推开,清洁地面后再把沙发推回原位。有同学认为,整个过程中沙发的位移为零,所以滑动摩擦力对沙发做的功也是零。这种观点是否正确?简述理由。
- “周一早上,小明提起书桌上的书包背到肩上,出门去学校。他坐电梯下楼后,走到一个十字路口正好遇到红灯,便站立等待。绿灯亮起后,小明加速通过横道线,走到校门口。进入校门后,他放慢脚步走向教学楼,然后走楼梯到达三楼的
教室。他走到自己的课桌前,从肩上取下书包并放到椅子下面,然后坐好等待上课。”在上述情景中,小明有时对书包做正功,有时对书包做负功,有时则不做功。从上述情景中选出有关实例并简述理由。
- 总质量 m = 2.0×103 kg 的电梯在钢绳的牵引下匀速上升至 h = 10 m 处,求此过程中钢绳拉力和电梯所受的重力分别做了多少功?这两个力做的总功是多少?
- 如图 7–11 所示,质量 m = 30 kg 的儿童从滑梯顶端 A 点滑下,经长 l = 12 m 的旋转滑道到达底端 B 点,A、B 两点间的水平距离 x = 4 m,高度差 h = 3 m。若下滑过程中阻力 F阻 的大小恒为 60 N,g 取 10 m/s2。求下滑过程中重力 G 和阻力 F阻 对儿童所做的总功。
- 如图 7–12 所示,长度 l = 1 m、质量 m = 5 kg 的均质硬杆一端由光滑铰链固定于天花板上的 O 点。在杆的另一端施加水平恒力 F = 10 N,使杆由竖直位置绕 O 点转过角度 θ = 37°,g 取 10 m/s2,求此过程中各力对杆所做的总功。
图 7–11
图 7–12
问题与思考解读
1.参考解答:不正确。公式 W = Fs 中,F 为恒力、s 为恒力作用下物体运动在力方向上的位移;而运动员对球的作用力 100 N 并未作用 10 m 全过程,故直接代入计算不正确。
命题意图:考查对功的计算式中位移的理解。
主要素养与水平:模型建构(Ⅰ);科学论证(Ⅰ)。
2.参考解答:不正确。公式 W = Fs 中,F 为恒力、s 为恒力作用下物体运动在力方向上的位移。而推开、推回过程中,滑动摩擦力的方向变化且总是与运动方向相反,殆终做负功,故虽然全过程位移为零,但滑动摩擦力对沙发做负功。
命题意图:考查对功的计算式中位移的理解。
主要素养与水平:模型建构(Ⅰ);科学论证(Ⅰ)。
3.参考解答:小明对书包做正功的情况有:提起书包的过程、加速前进的过程、走楼梯上楼的过程,这些过程中小明对书包的作用力与书包的运动方向同向或成锐角,根据 W = Fscosθ,可知做功为正。
做负功的情况有:乘电梯下楼的过程、放慢脚步的过程、取下书包放到椅子下面的过程,这些过程中小明对书包的作用力与书包的运动方向相反或成钝角,根据W = Fscosθ 知做功为负。
不做功的情况有:站立等待的过程、水平路面匀速前进的过程,这些过程中,或者书包的位移为零,或者小明对书包的作用力与书包的位移方向垂直,根据 W = Fscosθ 知做功为零。
命题意图:从文字表述中提取信息,结合真实情境辨析做功情况。
主要素养与水平:模型建构(Ⅱ);科学论证(Ⅰ)。
4.参考解答:对匀速上升的电梯受力分析,由平衡条件知
拉力 FT = G = mg = 2.0×103×9.8 N = 1.96×104 N
由恒力做功公式 W = Fscosθ 知
WT = FTh = 1.96×104×10 J = 1.96×105 J
WG = − Gh = − 1.96×104×10 J = − 1.96×105 J
总功 W总 = WT + WG =[1.96×105 + (− 1.96×105)] J = 0
命题意图:结合平衡条件分析做功情况。
主要素养与水平:模型建构(Ⅰ);科学推理(Ⅰ)。
5.参考解答:分析下滑过程,可知重力和阻力对儿童做功。
重力是恒力,由恒力做功公式 W = Fscosθ 知
WG = Gscosθ = Gh = mgh = 30×10×3 J = 900 J
阻力大小恒定、方向变化,始终与运动方向相反。由此可知阻力做负功,与路程成正比,路程近似取滑道长度 l
Wf = −F阻l = − 60×12 J = − 720 J
此过程中各力所做的总功
W总 = WG + W阻 =(900 − 720)J = 180 J
命题意图:将真实情境转化为模型化情境。
主要素养与水平:模型建构(Ⅱ);科学推理(Ⅰ)。
6.参考解答:杆转动过程中受到重力 G、恒力 F 和铰链对杆的作用力 FN,其中仅重力 G、恒力 F 做功。G 的作用点为重心,位于杆的中点,其上升高度 h = \(\frac{{1 \times (1 - \cos 37^\circ )}}{2}\) m ≈ 0.1 m。
由恒力做功公式 W = Fscosθ 知
WF = Flsinθ = 10×1×sin37° J = 6 J
WG = − mgh = − 5×10×0.1 J = − 5 J
W总 = WF + WG = [6 + (− 5) J = 1 J
命题意图:由求各个力做功转而求各力所做总功,深化对功的计算式中位移的理解。
主要素养与水平:模型建构(Ⅰ);科学推理(Ⅱ)。
发布时间:2022/2/9 下午10:59:00 阅读次数:7436
