第 1 章 功和机械能 第 1 节 机械功

用一定的力斜拉购物篮移动时（图 1-1），拉力方向与篮的位移方向有一定的夹角，拉力对篮做功了吗？在初中物理的基础上，本节我们进一步深化对功的认识，学习力与位移互成角度时功的计算。

1．机械功的含义

如果施力于某物体，并使该物体在力的方向上移动一段距离，我们就说力对这个物体做了功。如果作用于某物体的恒力大小为F，该物体沿力的方向运动的位移大小为 s，则 F 与 s 的乘积称为机械功（mechanical work），简称功，用 W 表示，其公式为

W = Fs

这个公式只适用于恒力方向与运动方向一致的情况。在生产生活中，我们经常见到类似斜拉购物篮的情景，这时作用于物体的力与物体的位移成一定夹角。在这个过程中，拉力做的功是多少呢？我们把斜拉购物篮这类情景转换为物理模型：物体在与水平方向成 α 角的恒定拉力 F 作用下沿水平方向移动，发生的位移是 s，在这个过程中，拉力 F 所做的功是多少？

如图 1-2 所示，可将 F 分解为沿水平方向向右的分力 F₁ 和沿竖直方向向上的分力 F₂ 。F₁ 与物体位移的方向一致，对物体做了功；F₂ 与物体位移的方向垂直，不对物体做功。因此，恒力 F 对物体所做的功 W 就等于分力 F₁ 所做的功。再结合功的定义，可得出恒力做功的计算公式

W = Fscos α

功只有大小没有方向，是标量。在国际单位制中，功的单位是焦耳，用符号 J 表示。如果 1 N 的力使物体在力的方向上发生了 1 m 的位移，那么这个力对该物体所做的功就是 1 J，即

1 J = 1 N × 1 m = 1 N·m

拓展一步

功的图像描述

我们也可用图像来描述力对物体做功的大小。当力的方向与位移方向一致时，以力 F 的大小为纵坐标、位移 s 的大小为横坐标，作出 F 随 s 变化的图像。

当 F 为恒力时，由 F 和 s 为邻边构成的矩形面积即表示功的大小，如图 1-3（a）所示。若 F 不是恒力，可将位移划分为若干等距的小段，在每个小段中 F 可近似看成恒力，其所做功的大小即为该小段对应的小矩形的面积，整个过程中 F 所做功的大小近似等于所有小矩形面积之和，如图 1-3（b）所示。

2．机械功的计算

由功的计算公式可知，当力 F 和物体位移 s 的大小都一定时，功 W 就由 F 与 s 的夹角  α 的余弦 cosα 决定。

当 α  = 0°时，cos α = 1，W = Fs，这就是初中物理中作用力与物体位移方向相同的情况。

当 α = 90° 时，cos α = 0，W = 0，表示力 F 与物体位移的方向垂直时，对物体不做功。

当 0° ≤ α < 90° 时，cos α > 0 ，W = Fscos α > 0，表示力 F 对物体做正功。

当 90° < α ≤ 180° 时， cos α < 0，W = Fscos α < 0，表示力 F 对物体做负功，也可说物体克服这个力做了功。

当 α  = 180° 时，cos α  = − 1，W = − Fs，表示作用力与物体位移方向相反。例如，在某些飞机着陆滑跑中，要打开尾部的减速伞（图 1-4）。在这个过程中，减速伞拉力的方向与飞机位移的方向相反，对飞机做负功，也可以说飞机克服这个拉力做了功。

当物体在多个外力共同作用下运动，求所有外力对物体做的总功时，需要逐个分析哪些力做功，哪些力不做功，哪些力做正功，哪些力做负功。功是标量，对功的叠加应采用求代数和的方法。所有外力对物体做的总功，等于各个力分别对物体做功的代数和，即

W_总 = W₁ + W₂ + W₃ + …

= F₁scosα₁ + F₂scosα₂ + F₃scosα₃ + …

可以证明，某个物体在多个外力作用下运动时，所有外力对这个物体做的总功，也等于这些外力的合力对该物体做的功，即

W_总 = F_合scosα

例题

一人用平行于斜面的推力把重 G ＝ 500 N 的货物从斜面底端推到斜面顶端。已知斜面的倾角 α ＝ 37°，斜面长 l ＝ 5 m，斜面与货物间的动摩擦因数 μ ＝ 0.2，推力 F ＝ 400 N。求货物从斜面底端运动到顶端的过程中，所受各力分别对其做的功，以及所有外力对其做的总功。（货物可视为质点，取 sin 37°＝ 0.6，cos 37°＝ 0.8）

分析

斜面上的货物受到重力 G、推力 F、支持力 N 和摩擦力 f 共四个力的作用，受力分析如图 1-5 所示。货物位移 s 的方向沿斜面向上，G 与 s 的夹角是 90° + α，N 与 s 的夹角是90°，f 与 s 的夹角是 180°。由功的计算公式可知各力做的功，再计算各力做功的代数和可知合外力做的功。

解

将货物视为质点，则其位移 s ＝ l ＝ 5 m。

推力 F 对货物做功

W₁ ＝ Fs ＝ 400×5 J ＝ 2 000 J

重力 G 对货物做功

W₂ ＝ G scos（90° + α） ＝ − Gssinα

＝ − 500×5×0.6 J

＝ − 1 500 J

支持力 N 对货物做功

W₃ ＝ Nscos 90° ＝ 0

摩擦力 f 对货物做功

W₄ ＝ fscos180° ＝ （μGcos α）scos 180°

＝ − 0.2×500×0.8×5 J

＝ − 400 J

所有外力对货物做的总功

W_总 ＝ W₁ + W₂ + W₃ + W₄

＝（2 000 − 1 500 + 0 − 400）J

＝ 100 J

讨论

求得所有外力对货物做的总功大于零，表明货物所受的动力大于阻力。

策略提炼

计算某力做功时，需先确定物体在该力的作用下发生的位移，找出力与位移的夹角 α，再运用 W ＝ Fscosα 计算该力所做的功。

计算合外力所做的功时，可分别计算每个力所做的功，再求其代数和；也可先求物体所受的合外力，然后计算合外力所做的功。具体采用哪种方法，应视题目情况而定。

迁移

上述问题中，能否先求出物体所受的合外力，再求出合外力做的功？试一试，看看计算结果是否相同。

节练习

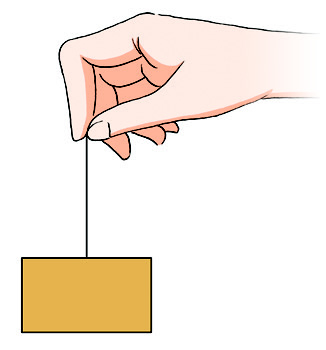1．如图所示，若用轻绳拴一物体，使物体以恒定加速度向下做减速运动，则下列说法正确的是（    ）

A．重力做正功，拉力做负功，合外力做正功

B．重力做正功，拉力做负功，合外力做负功

C．重力做正功，拉力做正功，合外力做正功

D．重力做负功，拉力做负功，合外力做负功

【参考解答】B

2．下列选项中，物体所受力 F 的大小相等，位移方向向右、大小相同。其中，F 做功最少的是（    ）

【参考解答】D

3．质量 m ＝ 2 kg 的物体，受到与水平方向成 37° 角斜向右上方、大小为 10 N 的拉力 F 的作用，在水平地面向右移动的距离 s ＝ 2 m，物体与地面间的滑动摩擦力 f ＝ 4.2 N。取 sin37° ＝ 0.6，cos37° ＝ 0.8，求在此过程中合外力对物体所做的功。

【参考解答】7.6 J

4．下列说法正确的是

A．静摩擦力一定不做功                   B．滑动摩擦力一定做负功

C．滑动摩擦力一定做正功               D．滑动摩擦力既可以做正功也可以做负功

【参考解答】D

5．关于作用力与反作用力做功，有同学认为：当作用力做正功时，反作用力一定做负功。你认为这种观点正确吗？请说明理由。

【参考解答】不正确。作用力与反作用力是发生在两个相互发生的物体之上的，作用力做正功时，反作用力可以做正功，可以不做功，还可以做负功。实际上，一对相互作用力做功的情况较多。例如，相互排斥的磁铁正在相互远离，一对排斥力均做正功；相向而行，正在靠近的两个带同种电荷的小球，一对排斥力均做负功；一对异种电荷，一个固定，另一个由静止释放，吸引力对一个电荷做正功，对另外一个电荷不做功等。

6．以一定的速度竖直向上抛出一小球，小球上升的最大高度为 h。假设空气阻力大小恒为 F，那么在小球被抛出至落回出发点的过程中，空气阻力对小球做的功为多少？

【参考解答】上升过程空气阻力对小球做功 W₁ = − Fh，下落过程空气阻力对小球做功 W₂ = − Fh，则从抛出到落回至抛出点的过程中，空气阻力对小球做的功 W = W₁ + W₂ = − 2Fh。

发布时间：2022/1/11 下午8:22:04  阅读次数：1853