第七章 第二节 交变电流

 

 

 

当今人类生存的环境是一个“电的世界”，我们的生活离不开电。从普通照明灯到节日彩灯，从电视机到洗衣机，从工厂机床到电气化高铁，从家用计算机到中国“天河三号 E 级”超级计算机系统，从电子收款机到自动化生产线都要用电。现代化的生产和生活都与电密切相关，没有电几乎寸步难行！而这些设备大多数是由交变电流供电，大型交流发电机产生的交变电流通过输电线向城市和农村源源不断输送强大的电能。

大小和方向都随时间做周期性变化的电流叫做交变电流（alternating current），简称为交流电。交变电流具有许多特点，在工农业生产和日常生活中有着广泛的应用。例如，交变电流能够通过变压器改变电压，使高效节能的远距离输电成为可能；交变电流能够形成旋转磁场，为交流电动机提供动力；在发电量相同的条件下，交流发电设备比直流发电设备更简单。图 7–13 为上海外高桥电厂具有国际先进水平的 1 000 MW 交流发电机组。

交变电流是如何产生的？

法拉第发现电磁感应现象的一个重大应用就是研制出发电机。交变电流来自交流发电机，图 7–14 是一个简易的交流发电机模型图。

 

 

在交流发电机模型中，有一个放在匀强磁场中的矩形线圈，线圈两端分别通过滑环、电刷与小灯泡相连。转动发电机的手柄，两个磁极之间的线圈随之转动，这时可以看到小灯泡一闪一闪地发光。如果将灵敏电流计串联在小灯泡的电路中，可以发现电流表的指针左、右摆动。说明发电机产生的是大小和方向都在不断变化的电流，这就是交变电流。

我们先用电压传感器来观察几种交流电的电压随时间变化的规律。

如图 7–15（a）所示，利用低频信号发生器输出“正弦”“方形”和“三角形”三种交流电的电压信号，用电压传感器采集各时刻的电压值，通过计算机显示这三种信号的电压随时间变化的波形。

 

图 7–15 采集几种交流电的电压随时间变化的图像

虽然交流电的电压随时间变化的规律是多种多样的，但如同简谐运动是一种最简单、最基本的振动一样，其中最重要、最基本的是按照正弦规律变化的交流电的电压。

图 7–16 为简易交流发电机模型的原理图。线圈在磁场中转动且切割磁感线而产生感应电动势。当转到线圈平面与磁场方向垂直位置 MN 时，由于线圈不切割磁感线，故此位置线圈的感应电动势为零。我们将该位置叫做中性面。

如果我们匀速转动简易交流发电机手柄，也能够得

 

到正弦交变电流，简称正弦交流电。如图 7–17 所示，为正弦交流发电机的原理示意图。

 

图 7–17 正弦交流发电机的原理示意图

 

从图中可以看出：线圈中的感应电动势随线圈平面跟中性面之间的夹角做周期性变化。在线圈转动一周的过程中，出现两次最大值（一次正值，一次负值，表示电动势方向相反）；线圈平面每经过中性面一次，电动势的方向就改变一次。

正弦交流电随时间变化的规律可以用如图 7–18 所示的图像表示。以线圈平面处于中性面时开始计时，交流电的电动势 e 按正弦规律相应变化。

正弦交流电任意时刻 t 的电动势可以表示为

\[e = {E_{\rm{m}}}\sin \omega t\]

其中 E_m 称为正弦交流电电动势的最大值，ω 称为交流电的角频率，也就是线圈旋转的角速度，ωt = θ 是产生正弦交流电的线圈从中性面转过的角度。线圈匀速转动一周，ωt 从 0 增加到 2π。

当负载为纯电阻用电器时，负载两端的电压 u 和通过负载的电流 i，也按正弦规律变化，即

\[u = {U_{\rm{m}}}\sin \omega t\]

\[i = {I_{\rm{m}}}\sin \omega t\]

式中 U_m 和 I_m 分别称为正弦交流电的电压和电流最大值，u、i 分别称为正弦交流电的电压和电流瞬时值。

1．最大值和有效值

从正弦交流电随时间变化规律中可以发现，交流电在一个周期内电压和电流是不断变化的，交流电一个周期内所能达到的最大值（也叫做交流电的峰值）表示交流电的电压高低或电流强弱。交流电的最大值在实际中有重要意义，例如，把电容器接在交流电的电路中，就需要知道交流电的电压最大值。电容器所能承受的电压要高于交流电的电压最大值，否则电容器就可能被击穿损坏。

在研究交流电的功率时，通常用有效值表示交流电产生的效果。交流电的有效值是根据电流的热效应来规定的：在相同的电阻上分别通过直流电流和交变电流，经过一个交变电流周期的时间，如果它们在电阻上所产生的热量相等的话，则把该直流电电流、电压的大小作为交变电流（交流电）电流、电压的有效值（effective value）。例如，某一交流电通过一段电阻丝，在一段时间（整数个交变电流周期）内产生的热量为 Q，如果改用 2 A 的直流电通过同样的电阻丝，在相同的时间内产生的热量也为 Q，那么，这一交流电电流的有效值就是 2 A。

计算表明，正弦交变电流的电动势、电压和电流的有效值 E、U 和 I 与它们的最大值E_m、U_m 和 I_m 之间分别存在如下的关系

\[\color{#945E55}E = \frac{{{E_{\rm{m}}}}}{{\sqrt 2 }} \approx 0.707{E_{\rm{m}}}\]

\[\color{#945E55}U = \frac{{{U_{\rm{m}}}}}{{\sqrt 2 }} \approx 0.707{U_{\rm{m}}}\]

\[\color{#945E55}I = \frac{{{I_{\rm{m}}}}}{{\sqrt 2 }} \approx 0.707{I_{\rm{m}}}\]

我们通常说家庭电路的电压是 220 V，就是指有效值。各种使用交流电的电器设备铭牌上所标注的额定电压和额定电流的数值（图 7–19），一般交流电压表和交流电流表测量的数值，也都是有效值。以后提到交流电的数值，凡没有特别说明的都是指有效值。

 

 

 

2．周期和频率

交流电的电动势、电压和电流都是周期性变化的。跟所有的周期性变化一样，交流电变化的快慢也可以用周期或频率来表示。我们把交流电完成一次周期性变化所需要的时间叫做交流电的周期，用符号 T 表示，单位是秒（s）。交流电完成周期性变化的次数与所用时间之比叫做交流电的频率，用符号 f 表示，单位是赫兹（Hz）。

在仅有一对磁极的情况下，线圈转一周，感应电动势也变化一周。这种情况下正弦交流电的电动势、电压和电流的角频率与角速度相等，即 ω = 2πf。我国工农业生产和生活用的是正弦交流电，频率统一为 50 Hz。美国和西欧国家交流电的频率为 60 Hz。

示例 一矩形线圈在匀强磁场中匀速转动。从经过中性面开始计时，每转一周需时 0.02 s，线圈中产生的感应电动势 e 与时间 t 的关系如图 7–21 所示的正弦函数。试求：

（1）这一感应电动势的最大值、有效值、周期和频率；

（2）写出这一感应电动势随时间变化的关系式。

 

分析：从感应电动势的图像中可以直接读出电动势的最大值和周期，然后再根据相关公式计算有效值和频率。

根据周期计算频率，结合感应电动势的最大值可以写出感应电动势随时间变化的关系式。

解：（1）从图中可以读出感应电动势的最大值 e_m = 28.28 V，根据有效值与最大值的关系式，可知电动势的有效值

E = \(\frac{{{e_{\rm{m}}}}}{{\sqrt 2 }}\) = \(\frac{{28.28}}{{\sqrt 2 }}\) ≈ 20 V

从图像可知感应电动势变化的周期 T = 0.02 s，频率

f = \(\frac{1}{T}\) = \(\frac{1}{{0.02}}\) Hz = 50 Hz

（2）因为线圈匀速转动，且从经过中性面开始计时，则 t 时刻线圈平面与中性面之间的夹角

θ = ωt = 2πft = 2π×50t = 100πt

所以，这一感应电动势随时间变化的关系式为

e = 28.28 sin ( 100πt ) V

 

本节编写思路

交变电流是生产和生活中最常用到的电流，而正弦交变电流又是最简单和最基本的交变电流。正弦交变电流产生的原理是电磁感应，由于交变电流不同于直流电，它对各种相关元件的作用也不同；因此本节既是前一章电磁感应理论的具体应用，又是教材后一节变压器原理的基础。

由于交变电流的电压、电流等物理量，其大小和方向都随时间做周期性变化，这就需要用一些特殊的物理量描述，借助于图像能对交变电流做全面、细致的形象化描述。如周期和频率表示交变电流周期性变化的快慢；峰值表明交变电流在变化过程中所能达到的最大数值，反映了交变电流的变化范围；有效值反映的是交变电流的热效应在时间上的平均效果。

本节的重点是运用电磁感应的基本知识，配合相应的演示实验，分析交变电流的产生过程，认识交变电流的特点及变化规律。交变电流的有效值是本节教学的重点，也是教学的难点。

正文解读

广义上讲，交变电流（交流电）是方向和大小随时间做周期性变化的电动势、电压和电流的统称。

 

如教材图 7 – 15 所示，用 DIS 电压传感器测量低频信号发生器输出的不同交流电压，通过演示实验，知道存在不同类型的交流电。

 

如教材图 7 – 17 所示，线圈绕OOʹ 轴逆时针匀速转动。

设在 t = 0 时刻，线圈处在垂直于磁感线的平面 MN 内（称为中性面）。时刻 t 转过的角度为 ωt。设 ab = cd = l，此时，导线 ab 和 cd 的速度大小均为 v，切割磁感线的分速度为 v₁ = vsinωt，根据“右手定则”导线 ab 中感应电动势的方向垂直于纸面向外，大小为

e_ab = Blv₁ = Blvsinωt

如果线圈匝数为 n，则有

e_ab = nBlvsinωt

导线 cd 中感应电动势的大小 e_cd 与 e_ab 大小相等，e_cd 的方向垂直于纸面向内。导线 ab 和 cd 旋转过程中分别产生的感应电动势相当于两个“电源”的串联，所以在时刻 t 整个线圈中的感应电动势为

e(t) = 2e_ab = 2nBlvsinωt

从上式可以看出，当 n、B、l、v 和 ω 一定时，感应电动势随时间按正弦函数做周期性变化。

 

中性面是指与磁场方向垂直的线圈平面，线圈处于中性面时线圈中的磁通量最大，但线圈中的感应电动势为零；当线圈每次转过中性面时，感应电动势的方向都将改变。

 

任意时刻的感应电动势又可以表示为

e(t) = E_msinωt

式中 E_m = 2nBlv 为感应电动势的最大值。

若外电路为纯电阻，电阻的阻值为 R，线圈本身的电阻为 r，根据闭合电路欧姆定律，感应电流随时间的变化为

i(t) = \(\frac{{{E_{\rm{m}}}}}{{R + r}}\) sinωt = I_msinωt

式中 I_m =  \(\frac{{{E_{\rm{m}}}}}{{R + r}}\) 是感应电流的最大值

外电路两端的电压（路端电压）随时间的变化为

u(t) = i(t)R = \(\frac{{{E_{\rm{m}}R}}}{{R + r}}\)sinωt = U_msinωt

式中 U_m =  \(\frac{{{E_{\rm{m}}R}}}{{R + r}}\) 是外电路两端电压的最大值。

三相交流电详见本节资料链接。

 

此处正弦交流电的有效值和峰值的关系，对其他波形的交变电流一般不成立。

有效值和最大值是反映交变电流强弱或电压高低的物理量。在计算交变电流平均功率和交变电流通过电阻产生的热功率时，应该用有效值。在选择电容器等元件的工作电压时，必须大于加在这个电容器上电压的峰值。

正弦交流电的有效值与最大值之间关系的推导详见本节资料链接。

 

高中阶段不要求推导正弦交流电的最大值和有效值之间的关系。此处设置“自主活动”目的是通过 DIS 系统中的电压传感器直接测量学生电源的输出电压，显示正弦交流电的电压随时间变化的图像，可从由图像拟合的函数表达式中直接读取其最大值和周期。再用数字多用表的交流电压挡直接测量学生电源输出端的电压，其显示的是正弦交流电压的有效值和周期。两个实验测量值相互验证，从而理解正弦交流电的最大值和有效值之间的关系。

 

此处设置 STSE 的目的说明电网的频率是统一规定的，变频空调改变的是输入到专用压缩机的频率。

在电力系统中，联系发电和用电设备间的设施及装置统称为电力网，简称电网。电网属于输送和分配电能的中间环节，它主要由联结成网的送电线路、变电所、配电所和配电线路组成。电网质量优劣的主要指标是电压的幅值、频率和波形。

问题与思考解读

1．参考解答：U_m = 220\({\sqrt 2 }\) V ≈ 311 V，每秒钟电流方向改变 100 次。

命题意图：理解交变电流最大值和有效值的关系，知道交变电流的频率。

主要素养与水平：模型建构（Ⅰ）；科学推理（Ⅱ）。

 

2．参考解答：不正确。在线圈平面转到中性面的瞬间，如图 7 – 17（a）所示，穿过线圈的磁通量最大，但是 ab 和 cd 边均没有切割磁感线，磁通量的变化率为零，因而线圈中感应电动势为零；在线圈平面跟中性面垂直的瞬间，如图 7 – 17（b）所示，穿过线圈的磁通量为零，但是 ab 和 cd 均垂直切割磁感线，磁通量的变化率最大，因而线圈中的感应电动势最大。

命题意图：理解中性面，以及磁通量、磁通量变化率和感应电动势之间的联系和区别。

主要素养与水平：模型建构（Ⅰ）；科学推理（Ⅱ）。

 

3．参考解答：摇动手柄使模型发电机的线圈在磁场中旋转，并切割磁感线，接通电路前输出功率为零，提供的机械功率只需要克服线圈转动产生的摩擦阻力。模型发电机接通电路后，提供的机械功率除了要克服线圈转动产生的摩擦阻力以外，还要提供通电线圈和负载的电功率，所以模型发电机在接通电路并输出电流后比接通电路前需要用更大的力摇动手柄。

命题意图：应用能量守恒定律解决实际发电机能量转化问题。

主要素养与水平：模型建构（Ⅰ）；科学推理（Ⅱ）；科学论证（Ⅱ）。

 

4．参考解答：电解电容器标注的“300 V”是该电容器能够接交流电的电压最大值，其有效值为 U = \(\frac{{{U_{{\rm{max}}}}}}{{\sqrt 2 }}\) = \(\frac{{300}}{{\sqrt 2 }}\) V ≈ 212.1 V。

命题意图：知道电容器标注的电压值是指能够接在电容器两端电压的最大值。

主要素养与水平：模型建构（Ⅰ）；科学推理（Ⅱ）。

 

5．参考解答：（１）U = \(\frac{{{U_{{\rm{max}}}}}}{{\sqrt 2 }}\) = \(\frac{{150}}{{\sqrt 2 }}\) V ≈ 106.1 V

（2）I = \(\frac{{{I_{{\rm{max}}}}}}{{\sqrt 2 }}\) = \(\frac{{30}}{{\sqrt 2 }}\) A ≈ 21.2 A

（3）P = UI = 106.1×21.2 W ≈ 2 249 W ≈ 2 250 W

命题意图：理解交变电流最大值、有效值和功率之间的关系。

主要素养与水平：模型建构（Ⅰ）；科学推理（Ⅱ）。

 

6．参考解答：（1）U_max = \({\sqrt 2 }\)U = \({\sqrt 2 }\)×220 V ≈ 311 V

（2）I = \(\frac{U}{I}\) = \(\frac{220}{11}\) A = 20 A

（3）E = UIt = 220×20×3 600 J ≈ 1.58×10⁷ J ≈ 4.4 kW·h

命题意图：理解交变电流最大值、有效值和消耗的电能之间的关系。

主要素养与水平：能量观念（Ⅰ）；模型建构（Ⅰ）；科学推理（Ⅱ）。

 

7．参考解答：如果灯泡（负载）的两端 A 和 B 接通交流电源。当 电流为正时，如果电流从 A 端流入负载，电流对负载做功，能量流入负载；当电流为负时，电流从 B 端流入负载，电流仍然对负载做功，能量还是流入负载，因此交流电在整个周期内都有能量提供给负载。

命题意图：根据交变电流的特点分析用电器的能量转化。

主要素养与水平：能量观念（Ⅰ）；模型建构（Ⅰ）；科学推理（Ⅱ）。

资料链接

三相交流电

如果在磁场里有三个互成一定角度的线圈同时转动，电路里就产生三个交变电动势，由此产生的交流电叫做三相交流电。

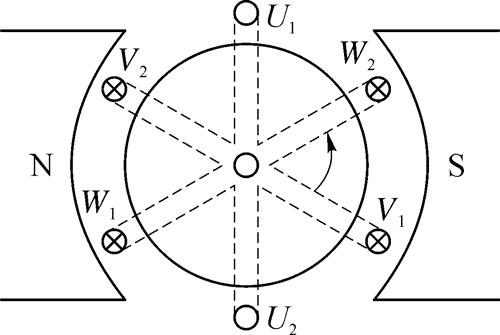
图 4 是三相交流发电机原理的示意图。在铁芯上固定着三个相同的线圈 U₁U₂、V₁V₂、W₁W₂，始端是 U₁、V₁、W₁，末端是 U₂、V₂、W₂，三个线圈平面互成 120° 角。当三个线圈在匀强磁场里做匀速转动 时，就会产生三个频率和最大值都相同，但“步调”不同的交流电动势。由于三个线圈的平面依次相差 120° 角，则它们感应电动势达到零值（中性面）和最大值（跟磁场方向平行）的时间，依次落后周期。如果取如图 4 所示的瞬间作为时间的起点，即 t = 0 时线圈 U₁U₂ 位于中性面上，三个线圈里的感应电动势就如图 5 中的三条正弦曲线所示。

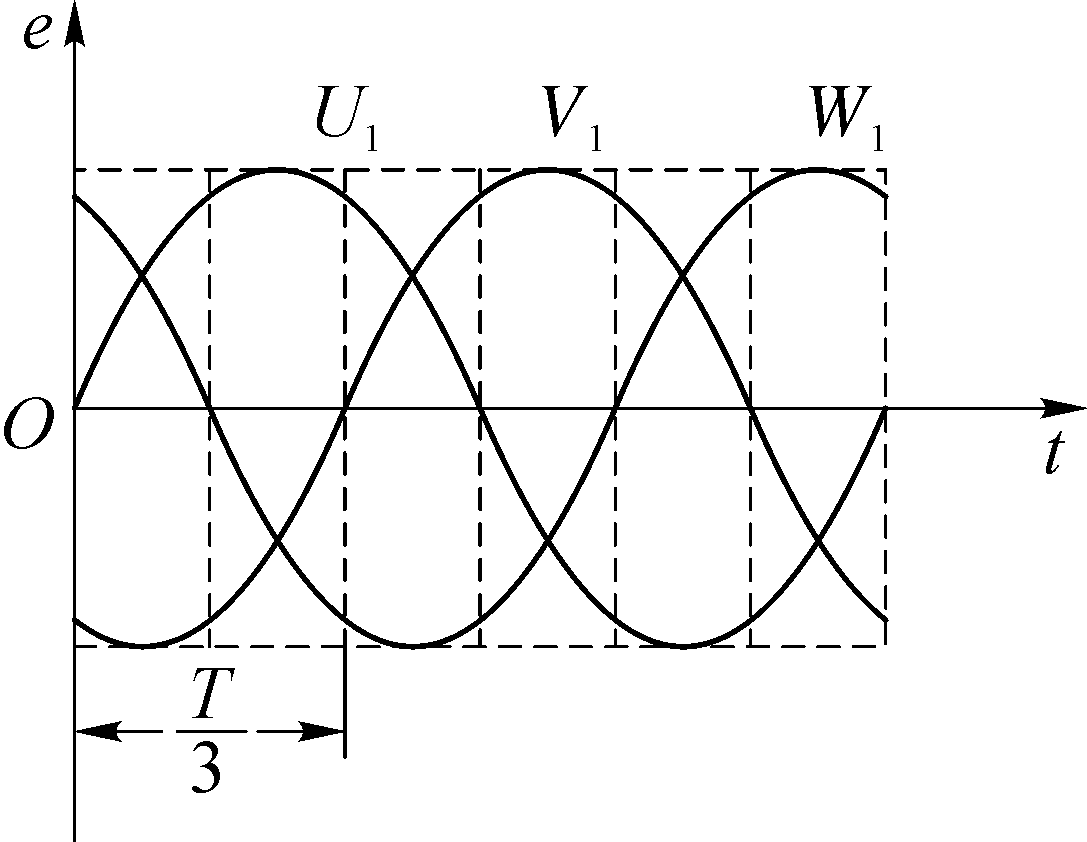
正弦交流电的有效值与最大值之间的关系

正弦交流电的有效值与最大值的关系可以用数学方法推导。设通过电阻的交流电瞬时值为 i = I_msinωt，则在 dt 时间内产生的热量是 dQ = i²Rdt，这是因为在极短时间 dt 内，交流电的变化很小，可以认为流经阻值为 R 的纯电阻的电流值 i 是不变的，所以可用直流电的公式计算。因此，在一个周期 T 内所产生的热量为

\[Q = \int_0^T {{\rm{d}}Q}  = \int_0^T {{i^2}R{\rm{d}}t}  = R\int_0^T {{i^2}{\rm{d}}t} \]

如果直流电流 I 通过同一个电阻，在相同时间（T）内所产生的热量为

Q′ = I²RT

根据交流电有效值的定义，若 Q′ = Q 则

\[{I^2}RT = R\int_0^T {{i^2}{\rm{d}}t} \]

由此式得，交流电的有效值可表示为瞬时值的方均根值

\[I = \sqrt {\frac{1}{T}\int_0^T {{i^2}{\rm{d}}t} } \]

若该交流电为正弦交流电，即交变电流为 i = I_msinωt，代入上式

则

\[\begin{array}{l}I = \sqrt {\frac{1}{T}\int_0^T {I_{\rm{m}}^2{{\sin }^2}\omega t{\rm{d}}t} }  = {I_{\rm{m}}}\sqrt {\frac{1}{{2T}}\int_0^T {(1 - \cos 2\omega t){\rm{d}}t} } \\ = \left. {{I_{\rm{m}}}\sqrt {\frac{1}{{2T}}\left( {t - \frac{{\sin 2\omega t}}{{2\omega }}} \right)} } \right|_0^T = \frac{{{I_{\rm{m}}}}}{{\sqrt 2 }} \approx 0.707{I_{\rm{m}}}\end{array}\]

同理，正弦交流电的电压有效值为

\[\begin{array}{l}U = \sqrt {\frac{1}{T}\int_0^T {{u^2}{\rm{d}}t} }  = \sqrt {\frac{1}{T}\int_0^T {U_{\rm{m}}^2{{\sin }^2}\omega t{\rm{d}}t} }  = {U_{\rm{m}}}\sqrt {\frac{1}{{2T}}\int_0^T {(1 - \cos 2\omega t){\rm{d}}t} } \\ = \left. {{U_{\rm{m}}}\sqrt {\frac{1}{{2T}}\left( {t - \frac{{\sin 2\omega t}}{{2\omega }}} \right)} } \right|_0^T = \frac{{{U_{\rm{m}}}}}{{\sqrt 2 }} \approx 0.707{U_{\rm{m}}}\end{array}\]

所以，正弦交流电的有效值等于其最大值的 \(\frac{1}{{\sqrt 2 }}\) 倍。