第 3 章 第 2 节 交变电流的产生

交变电流的大小和方向都随时间发生变化。它究竟是怎样产生的呢？本节我们将从交变电流的产生原理入手，学习其变化规律。

1．交流发电机

由法拉第电磁感应定律可知，只要通过闭合回路的磁通量发生变化，就可产生感应电动势和感应电流。发电机就是利用这一原理把机械能转变成电能的装置。

发电机主要由线圈（电枢）和磁极两部分组成，磁极有的使用永久磁铁，有的使用电磁铁。磁极固定不动，让电枢在磁极中旋转，使穿过线圈的磁通量发生变化而产生感应电动势，这种发电机被称为旋转电枢式发电机。电枢固定不动，让磁极在电枢中旋转，使穿过线圈的磁通量发生变化而产生感应电动势，这种发电机被称为旋转磁极式发电机。不论哪一种发电机，转动的部分都称为转子，固定不动的部分都称为定子。图 3-5 是一种早期的手摇交流发电机，当手柄转动时，就会有交变电流产生。

迷你实验室

用发电机产生交变电流

如图 3-6 所示，将发电机的两个输出端通过滑动变阻器连接到电流计的两个接线柱上，摇动发电机手柄，让线圈在两磁极间连续转动，注意观察电流计指针的偏转情况。

由实验可看出，发电机产生的感应电流的大小和方向是不断变化的。仔细观察可发现，线圈在磁场中转动时，感应电流的大小和方向都随时间做周期性变化，线圈每转动一周，电流方向改变两次。这种能产生大小和方向随时间做周期性变化电流的发电机，称为交流发电机。

2．正弦式交变电流的产生原理

交流发电机是如何产生大小和方向都随时间做周期性变化的电流的？

我们把手摇发电机的多匝线圈等效为一个矩形线圈，两个磁极产生的磁场近似视为匀强磁场（图 3-7）。矩形线圈的两个端头分别连接金属滑环 K 和 L，两个滑环又分别跟电刷 E 和 F 接触，并与外电路组成一个闭合回路。矩形线圈 abcd 在磁场中绕轴 OOʹ 匀速转动，ab 和 cd 边在切割磁感线时，使线圈中产生感应电动势，线圈和外部构成的闭合回路中就有了感应电流。请分析导线 ad 和 bc 是否会产生感应电动势。

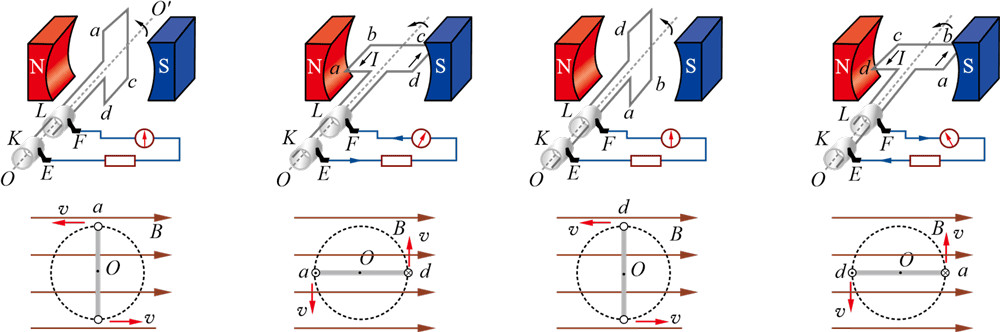
当线圈转到图 3-7（a）所示的位置时，线圈平面与磁感线垂直。在这一瞬间，ab 边和 cd 边的速度方向均与磁感线平行，线圈的这两边都不切割磁感线，因此不产生感应电动势，回路中没有感应电流。物理学中，把这个位置称为中性面。

当线圈沿逆时针方向转过 90° 到达图 3-7 （b）所示的位置时，线圈平面与磁感线平行。这时，ab 边向下切割磁感线，而 cd 边向上切割磁感线，根据右手定则可判定，线圈中的感应电流方向是 d → c → b → a。

当线圈继续转过 90° 到达图 3-7（c）所示的位置时，线圈平面与磁感线垂直，又到了中性面上。在这一瞬间，线圈的 ab 和 cd 两边都不切割磁感线，感应电流为零。

当线圈又继续转过 90°到达图 3-7（d）所示的位置时，线圈平面又与磁感线平行。这时，ab 边向上切割磁感线，而 cd 边向下切割磁感线，根据右手定则可判定，线圈中的感应电流方向是 a → b → c → d。

当线圈继续转过 90° 时，就回到图 3-7（a）所示的位置，又回到中性面上，感应电流为零，交变电流完成了一次周期性变化。接下来，线圈将重复上述转动过程，线圈中的电流也将重复上述变化过程。

物理聊吧

请从磁通量变化的角度，说明线圈在磁场中连续转动时，感应电流的大小和方向都会随时间做周期性变化的原因。

与同学讨论交流你的想法。

通过以上分析可知，在线圈连续转动过程中，感应电流的大小和方向都将随时间做周期性变化。线圈每经过中性面一次，感应电流的方向就改变一次；线圈每转动一周，感应电流的方向就改变两次。因为感应电流是由感应电动势引起的，所以线圈转动所产生的感应电动势也随时间做周期性变化。

3．正弦式交变电流的变化规律

感应电动势和感应电流随时间的变化究竟遵循怎样的规律？

如图 3-7 和 3-8 所示，设矩形线圈 ab 边的长度是 l，ad 边长为 l'，磁场的磁感应强度为 B。若线圈在磁场中从中性面开始以角速度 ω 匀速转动，经过时间 t 之后，线圈平面转过的角度 θ = ωt。这时，线圈 ab 边的线速度 v = \(\frac{1}{2}\)ωl'，其在垂直磁感线方向的分量 vsin θ = \(\frac{1}{2}\)ωl'sin ωt。因此，线圈 ab 边产生的感应电动势 e_ab = \(\frac{1}{2}\)Blωl'sin ωt = \(\frac{1}{2}\)BωSsin ωt （S 为线圈所围面积）。同理，在线圈 cd 边也会产生与 ab 边产生的大小相等的感应电动势。又因为在矩形线圈中 ab 边与 cd 边的电动势是同向串联的，所以在这一瞬间，整个线圈所产生的感应电动势 e = BωSsin ωt。如果线圈是由 n 匝相同的矩形线圈组成，则

\[e = nB\omega S\sin \omega t\]

当线圈平面转到与磁感线平行的位置时，线圈 ab 边和 cd 边的线速度方向都跟磁感线垂直，这时 ωt = \(\frac{\pi }{2}\)，sin ωt = 1，感应电动势达到最大值，用 E_m 来表示，即 E_m = nBSω。

因此，感应电动势随时间变化的规律又可表示为

\[e = {E_m}\sin \omega t\]

上式表明，当 n、B、l、ω 一定时，感应电动势随时间按正弦规律变化，在不同的时刻，e 具有不同的数值，被称为感应电动势的瞬时值（instantaneous value）。

在只含有电阻的交流电路中，欧姆定律也适用。如果回路的总电阻为 R，那么根据欧姆定律，回路中感应电流的瞬时值为

\[i = \frac{e}{R} = \frac{{{E_m}}}{R}\sin \omega t\]

式中，\(\frac{{{E_m}}}{R}\) 是感应电流的最大值，用 I_m 表示。因此，感应电流的瞬时值可表示为

\[i = {I_m}\sin \omega t\]

即感应电流也随时间按正弦规律变化。

如果这样的交变电流通过一段电阻为 R′ 的导体，那么该导体两端电压的瞬时值 u = iR′ = I_mR′sin ωt，其中 I_mR′ 是电压的最大值，用 U_m 表示。该导体两端的电压瞬时值可表示为

\[u = {U_m}\sin \omega t\]

即电路中的电压同样随时间按正弦规律变化。

例题

在匀强磁场中有一矩形线圈，绕线圈平面内垂直于磁感线的轴匀速转动。线圈中产生的感应电动势随时间变化的图像如图 3-9 所示，试求出该感应电动势的最大值、有效值、周期和频率，写出该感应电动势随时间变化的关系式。

分析

从图 3-9 可看出，感应电动势随时间按正弦规律变化，电动势的最大值为 10 V、周期为 2.0 × 10⁻² s，由此可求出有效值和频率，进而算出角速度，得出关系式。

解

电动势的最大值

E_m = 10 V

有效值

E = \(\frac{{{E_m}}}{{\sqrt 2 }}\) = \(\frac{{10}}{{\sqrt 2 }}\) V = 7.07 V

电动势的周期

T = 0.02 s

频率

f = \(\frac{1}{T}\) = \(\frac{1}{{0.02}}\) Hz = 50 Hz

ω = \(\frac{{2\pi }}{T}\) = 100π rad/s

所以，感应电动势随时间变化的表达式为

e = 10sin 100πt V

讨论

根据感应电动势瞬时值表达式，当 t = 0.5×10⁻² s 时，得到 e = 10sin \(\frac{\pi }{2}\) V = 10 V，与图像相符。此时，线圈平面与磁场方向平行，磁通量为零，感应电动势最大。

策略提炼

由图像确定交变电流的特征量和表达式时，可直接从图像读出最大值、周期，再由相关关系求出其他特征量。确定最大值和周期时要注意弄清坐标轴表示的物理量及其单位。

确定表达式时，要注意图像与瞬时表达式的关系，计时起点决定表达式是正弦函数还是余弦函数。

迁移

在上例中，如果以 t = 0.5×10⁻² s 为计时起点，其他条件不变，写出感应电动势随时间变化的关系式。

拓展一步

交变电流的相位

如果我们从线圈平面转到与中性面成某一夹角 φ₀ 的位置开始计时，那么经过时间 t 之后，线圈平面跟中性面之间的夹角就是 ωt + φ₀（图 3-10），这时交变电动势瞬时值为 e = E_m sin（ωt + φ₀），它的大小和方向都随时间不断变化。在 E_m 一定时，瞬时值不完全由时间 t 决定，而是由 ωt + φ₀ 决定，ωt + φ₀ 称为交变电流的相位或相。t = 0 时的相 φ₀ 称为初相。相位不仅可反映交变电流任何时刻的状态，还可用来比较不同交变电流的变化步调。

图 3-11 表示两个频率相同但初相不同的交变电流，φ₁ > φ₂。由图可看出，这两个交变电流的变化步调不一致，i₁ 比 i₂ 先到达正的最大值、零值或负的最大值，这时我们说 i₁ 比 i₂ 超前 Δφ = φ₁ − φ₂，或者说 i₂ 比 i₁ 滞后 Δφ。

节练习

1．有同学认为：在匀强磁场中，矩形线圈绕线圈平面内垂直于磁感线的轴匀速转动时，线圈平面跟中性面垂直的瞬间，穿过线圈的磁通量为零，因此线圈中的感应电动势为零；线圈平面在中性面内的瞬间，穿过线圈的磁通量最大，因此线圈中的感应电动势最大。这种看法正确吗？为什么？

【参考解答】不正确。磁通量变化越快，感应电动势越大。

2．一个矩形线圈在匀强磁场中转动，产生的感应电动势大小为 e = 220\(\sqrt 2 \) sin100 πt V，则

A．交变电流的频率是 100π Hz                  B．t = 0 时，线圈位于中性面

C．交变电流的周期是 0.02 s                       D．t = 0.05 s 时，e 有最大值

【参考解答】BC

3．图（a）为风力发电的简易模型，在风力的作用下，风叶带动与其固定在一起的永磁体转动，转速与风速成正比。某一风速时，线圈中产生的正弦式交变电流如图（b）所示，则

A．电流的表达式为 i = 0.6 sin10πt A

B．磁铁的转速为 10 r/s

C．风速加倍时，电流的表达式为 i = 1.2 sin10πt A

D．风速加倍时，线圈中电流的有效值为 1.2 A

【参考解答】A

4．如图所示，一个电阻为 r、边长为 l 的正方形线圈 abcd 共 n 匝，线圈在磁感应强度为 B 的匀强磁场中绕垂直于磁感线的轴 OOʹ 以角速度 ω 匀速转动，外电路电阻为 R。

（1）判断图示位置电路中的电流方向；

（2）求线圈从图示位置转过 60° 时的感应电动势；

（3）线圈转动过程中，电压表的示数为多大？

【参考解答】（1）b→a→d→c（或从上到下流过电阻 R）

（2）e₀ = \(\frac{1}{2}\)nBl²ω

（3）U = \(\frac{{nB{l^2}\omega R}}{{\sqrt 2 R + r}}\)

5．小型发电机内的矩形线圈在匀强磁场中以恒定的角速度绕垂直于磁场方向的固定轴转动，线圈匝数 n = 100，穿过线圈的磁通量随时间按正弦规律变化，如图所示。已知发电机内阻 r = 5.0 Ω，外电路电阻 R = 95 Ω，感应电动势的最大值 E_m = nωΦ_m，其中 Φ_m 为穿过每匝线圈磁通量的最大值。不计电流表的内阻，求串联在外电路中的电流表的读数。

【参考解答】I = \(\sqrt 2 \) A

*6．海洋中蕴藏着巨大的能量，利用海洋的波浪可以发电。在我国南海上有一浮桶式波浪发电灯塔，其原理如图（a）所示。浮桶内的磁体通过支柱固定在暗礁上，浮桶内置线圈随波浪相对磁体沿竖直方向运动，且始终处于磁场中，该线圈与阻值 R = 15 Ω 的灯泡相连。浮桶下部由内、外两密封圆筒构成（图中黄色部分），如图（b）所示，其内为产生磁场的磁体，与浮桶内侧面的缝隙忽略不计；匝数 N = 200 的线圈所在处辐射磁场的磁感应强度 B = 0.2 T，线圈直径 D = 0.4 m，电阻 r = 1 Ω。取重力加速度 g = 10 m/s²，π² = 10。若浮桶随波浪上下运动的速度可表示为 v = 0.4πsin πt m/s，求：

（1）波浪发电产生电动势 e 的瞬时值表达式；

（2）灯泡两端电压的有效值和灯泡的电功率。

【参考解答】（1）e = 64sinπt

（2）30\(\sqrt 2 \) V，120 W

发布时间：2022/12/7 下午10:37:56  阅读次数：3762