第三章 第 1 节 交变电流
3
第三章
交变电流
公路旁、旷野上,坚实的钢架托着、吊着粗大的金属线,仿佛由天际而来,向天际而去……
这些由发电厂、变电站而来的输电线,将电能输送到乡村、工厂,输送到千家万户。电,每时每刻都在为人类作着巨大的贡献。
来自发电厂的电有什么特性?我们怎样才能更好地利用它?这一章我们就来学习与此相关的内容。
把高压电流在能量损失较小的情况下通过普通电线输送到迄今连想也不敢想的远距离,并在那一端加以利用……这一发现使工业几乎彻底摆脱地方条件所规定的一切界限,并且使极遥远的水力的利用成为可能,如果在最初它只是对城市有利,那么到最后它终将成为消除城乡对立的最强有力的杠杆。①
——恩格斯
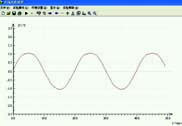
用示波器或电压传感器先观察电池供给的电压的波形,再观察学生电源交流挡供给的电压的波形。这两种波形各有什么特点?

如图 3.1–1 所示,在显示屏上显示的电压(或电流)随时间变化的图像,在电工技术和电子技术中常常叫作波形图。
我们已经学过了恒定电流。在恒定电流的电路中,电源的电动势不随时间变化,电路中的电流、电压也不随时间变化。但是在供给工农业生产和日常生活用电的电力系统中,发电机产生的电动势是随时间做周期性变化的,因而,很多用电器中的电流、电压大小和方向也随时间做周期性变化,这样的电流叫作交变电流(alternating current,AC),简称交流。方向不随时间变化的电流称为直流(direct current,DC)。电池供给的电流方向不随时间变化,所以属于直流。
① 引文摘自《马克思恩格斯全集》第 35 卷第 446 页,人民出版社 1971 年第 1 版。
交变电流经过电子电路的处理,也能变成直流,学校实验室的学生电源就有这种功能。日常使用的各种充电器能把交变电流变成低压直流。
观察交变电流的方向
把两个发光颜色不同的发光二极管并联,注意使两者正、负极的方向不同,然后连接到教学用发电机的两端(图 3.1–2)。转动手柄,两个磁极之间的线圈随着转动。观察发光二极管的发光情况。
实验现象说明了什么?

教学用发电机产生的电流,大小和方向都在不断地变化,是一种交变电流。图 3.1–3 是交流发电机的示意图。装置中两磁极之间产生的磁场可近似为匀强磁场, 为了便于观察,图中只画出了其中的一匝线圈。线圈的 AB 边连在金属滑环 K 上,CD 边连在滑环 L 上;导体做的两个电刷 E、F 分别压在两个滑环上,线圈在转动时可以通过滑环和电刷保持与外电路的连接。

假定线圈沿逆时针方向匀速转动,如图 3.1–3 所示。 我们考虑下面几个问题。
1.在线圈由甲图转到乙图所示位置的过程中,AB 边中电流向哪个方向流动?
2.在线圈由丙图转到丁图所示位置的过程中,AB 边中电流向哪个方向流动?
3.转到什么位置时线圈中没有电流,转到什么位置时线圈中的电流最大?
可以根据右手定则来判断线圈运动时,AB 边或 CD 边上感应电流的方向。因为 AB 边或 CD 边运动时,垂直于磁感线方向的速度不断变化,所以感应电动势也在变化,感应电流同时发生变化。假设电流从 E 经过负载流向 F 的方向记为正,反之为负,在横坐标轴上标出线圈到达图 3.1–3 中甲、乙、丙、丁几个位置时对应的时刻(图 3.1–4),大致画出感应电流随时间变化的曲线。
从图 3.1–1 看出,学生电源中的交变电流似乎在按照正弦函数的规律变化,实际情况正是如此。
对于图 3.1–3 所示的发电机,设 t = 0 时线圈刚好转到中性面(如甲图)位置,此时导线 AB 的速度方向刚好与磁感线平行,因此感应电动势为 0。设线圈旋转的角速度为 ω,AB 和 CD 的长度为 l,AD 和 BC 的长度为 d,则经过时间 t,线框转过的角度 θ = ωt,如图 3.1–5 所示。线框旋转


过程中 AB 和 CD 的速度 v = ω \(\dfrac{d}{2}\),与磁感线垂直的速度为 vsin θ,即 \(\dfrac{{\omega d}}{2}\) sin ωt。根据法拉第电磁感应定律,线框上产生的感应电动势
e = 2Blvsin θ = ωBldsin ωt = ωBSsin ωt
其中,S 表示线框的面积。
设 Em = ωBS,可知线框的电动势是随时间按正弦函数规律变化的,为
\[\tag{1}\label{1}e = {E_m}\sin \omega t\]
式中 Em 是常数,表示电动势可能达到的最大值。对于单匝线圈,Em = ωBS;如果线圈匝数为 N,则 Em = NωBS。
由于图 3.1–3 所示发电机的电动势按正弦规律变化,所以当负载为电灯等纯电阻用电器时,负载两端的电压 u、流过的电流 i,也按正弦规律变化,即
\[\tag{2}\label{2}u = {U_m}\sin \omega t\]
\[\tag{3}\label{3}i = {I_m}\sin \omega t\]
式中 Um 和 Im 分别是电压和电流的最大值,也叫峰值(peak value),而 e、u、i 则是相应的物理量的瞬时值。这种按正弦规律变化的交变电流叫作正弦式交变电流,简称正弦式电流(sinusoidal current)。图 3.1–6 是正弦式交变电流电动势 e、电流 i 和电压 u 随时间变化的图像。
正弦式电流是最简单、最基本的交变电流。电力系统中应用的大多是正弦式电流(图 3.1–7 甲)。在电子技术中也常遇到其他形式的交流,如图 3.1–7 乙、丙所示。
发电厂里的交流发电机的构造比图 3.1–3 复杂得多,但是基本组成部分也是两部分,即产生感应电动势的线圈(通常叫作电枢)和产生磁场的磁体。电枢转动,磁极不动的发电机,叫作旋转电枢式发电机。如果磁极转动,电枢不动,线圈中同样会产生感应电动势,这种发电机叫作旋转磁极式发电机。不论哪种发电机,转动的部分都叫转子,不动的部分都叫定子。


旋转电枢式发电机转子产生的电流,必须像图 3.1–3 那样经过裸露的滑环和电刷引到外电路,如果电压很高,可能发生火花放电,滑环和电刷很快会烧坏。同时,转动的电枢无法做得很大,线圈匝数也不可能很多,所以产生的感应电动势也不能很高。这种发电机输出的电压一般不超过 500 V。旋转磁极式发电机克服了上述缺点,能够产生几千伏到几万伏的电压,输出功率可达几百兆瓦。所以,大多数发电机是旋转磁极式的。
发电机的转子(图 3.1–8)由蒸汽轮机、水轮机等带动。蒸汽轮机、水轮机等将机械能传递给发电机,发电机将机械能转化为电能,输送给外电路。

1.有人说,在图 3.1–3 中,线圈平面转到中性面的瞬间,穿过线圈的磁通量最大,因而线圈中的感应电动势最大;线圈平面跟中性面垂直的瞬间,穿过线圈的磁通量为 0,因而感应电动势为 0。这种说法对不对?为什么?
2.图 3.1–3 中,设磁感应强度为 0.01 T,单匝线圈边长 AB 为 20 cm,宽 BC 为 10 cm,转速 n = 50 r/s,求线圈转动时感应电动势的最大值。
3.一台发电机产生正弦式电流。如果发电机电动势的峰值 Em = 400 V,线圈匀速转动的角速度 ω = 314 rad/s,试写出电动势瞬时值的表达式(设 0 时刻电动势瞬时值为 0)。如果这台发电机的外电路只有电阻元件,总电阻为 2 kΩ,电路中电流的峰值为多少?写出电流瞬时值的表达式。
4.如图 3.1–9 所示,KLMN 是一个竖直的矩
形导线框,全部处于磁感应强度为 B 的水平方向的匀强磁场中,线框面积为 S,MN 边水平,线框绕某一竖直固定轴以角速度 ω 匀速转动。在 MN 边与磁场方向的夹角到达 30° 的时刻(图示位置),导线框中产生的瞬时电动势 e 的大小是多少?标出线框此时的电流方向。已知线框按俯视的逆时针方向转动。

第三章 交变电流
课程标准的要求
2.2.4 通过实验,认识交变电流。能用公式和图像描述正弦交变电流。
2.2.5 通过实验,探究并了解变压器原、副线圈电压与匝数的关系。知道远距离输电时通常采用高压输电的原因。
2.2.6 了解发电机和电动机工作过程中的能量转化。认识电磁学在人类生活和社会发展中的作用。
本章教材概述
第一、二章研究的是磁场对电流或电荷的作用以及电磁感应的关知识,本章主要研究交变电流的特征和规律、交变电流的描述方法、改变交变电流电J玉的变压器和交变电流的输送等问题。本章是电磁感应的应用性知识,与生产生活联系非常紧密,凶此既有理论建构的难度也有实际应用的价值。本章可以有效地培养学生理论模型建构的能力和运用理论解释和解决实际问题的能力。相比 2004 年版《普通高中课程标准实验教科书物理》,本章在教材编写上做了一砦改进。
第一,因为课时调整的关系,从物理学科核心素养的培养考虑,要突出主干知识,删除次要知识,把“电感器和电容器对交变电流的作用”这一内容,放在了非正文的“拓展学习”栏目。
第二,在第 1 节“交变电流”中做了一些改变。一是为了增加学生对交变电流的大小与方向的学习感悟,引导学生的自主学习,增加了按发电机的旋转过程逐步分析并表达线圈上电流的大小和方向这样一个课堂活动。这个活动的意图是让学生能够自己进行发电机原理的阶段性分析,并且能够用定性与定量相结合的方法把电流的变化过程记录下来,以加深对交变电流的认识。二是为了增强学生的模型分析和推理能力,增加了让学生运用法拉第电磁感应定律分析和推理出矩形线圈在磁场中旋转时所产生的感应电流(即交变电流)的表达式。这个推理过程有一定的难度,目的是让学生运用法拉第电磁感应定律来推导线圈上瞬时电流的表达式,同时能够深度理解描述交变电流的几个特征量的意义。三是把交流发电机的内容从“科学漫步”栏目变成正文内容,主要意图是更注重发电机这样的应用性内容,培养学生关注实际问题的意识和解决实际问题的能力。
第三,在第 2 节“交变电流的描述”中,删除了相位和相位差这两个概念。主要原因一是课时要求,二是相位与相位差的概念比较抽象,而且除了电容与电感内容之外也没有具体的应用,三是从知识的性质来说这两个概念的缺席不影响后面内容的学习。
第四,加强了交变电流的应用,在应用性的学习材料上主要是增加了无线充电技术的介绍,因为无线充电技术近年未发展很快,应用越来越普及,而对其原理的理解并不难。
具体来说,本书编写时有以下一些思考。
1.深化对主干知识的学习
本章内容主要介绍的是交变电流的概念、描述方法、变压器及电能的输送等问题。第 1 节中为了让学生对交变电流的产生原理有深入理解,特意安排了一个线圈在匀强磁场中旋转产生感应电流的推理计算内容。推理过程既可以让学生对发电机的模型有深入理解,也可以对发电机的发电原理和感应电流的特征有更深的理解。同时,为了强化学生对发电机发电过程的探究与过程性认知,安排了用图像表达发电机产生的电流变化规律的学生活动,这使学生在探究发电机旋转过程中磁通量、感应电动势和感应电流等物理量之间的关系时能深入地思考和认识。
对这些主干知识的深入学习有助于学生模型建构和模型理解能力的提升,也有助于学生推理能力的提升。这样的教材编写方式主要意图在于培养学生学科能力的发展。
2.加强知识的实际应用
交变电流与生产生活的联系非常紧密,包括电磁感应相关知识的应用和交变电流的产生、输送和实际应用。本章应注重几个重要的应用:交变电流的产生原理、变压器改变交变电流的电压、电能的输送等,在拓展性学习内容中还安排上,电容器与电感器对交变电流的作用和影响、直流输电和无线充电技术等。要让学生体会现代社会电的运用的广泛性和普及性,交变电流本身的应用性内容很多,家用电器大多离不开交变电流。
课时安排建议
第 1 节 交变电流 1 课时
第 2 节 交变电流的描述 1 课时
第 3 节 变压器 2 课时
第 4 节 电能的输送 1 课时
第 1 节 交变电流 教学建议
1.教学目标
(1)通过实验认识交变电流,知道生产生活中使用的大多足正弦式交变电流,会用图像和公式描述正弦式交变电流。
(2)经历建立正弦式交变电流模型、用右手定则和法拉第电磁感应定律推理得出正弦式交变电流方向和大小的规律的过程,体会建立模型与推理分析的思维方法。
(3)了解发电机是将机械能转化为电能的装置,各种发电机的区别在于机械能产生的形式不同。
2.教材分析与教学建议
在生产生活中普遍使用交变电流,而正弦式交变电流又是最简单和最基本的交变电流。正弦式交变电流的产生是基于电磁感应的相关知识,所以本章是前一章的延续和发展,是电磁感应理论的具体应用。由于交变电流与直流不同,各种元件在交变电流和直流电路中的作用也不同。正因为交变电流的特殊性,才有了变压器及其广泛的应用。所以,本节内容起到了承上启下的作用。
本节的教学重点是运用电磁感应的相关知识分析交流发电机产生交变电流的过程。通过“问题”、相应的演示实验、“思考与讨论”等栏目.使学生建立正弦式交变电流的模型,用右手定则和法拉第电磁感应定律分析推理得出正弦式交变电流方向和犬小变化的特点,体会建立模型与推理分析的思维方法。这个推理过程也是一个教学难点。要引导学生在具体情境中运用法拉第电磁感应定律分析和推导矩形线圈在匀强磁场中旋转时所产生的感应电流(即交变电流)的表达式和图像,理解描述交变电流的几个特征量的意义。
具体教学内容展开的流程框图如下:

(1)问题引入
教材在节前的“问题”栏目提出:“用示波器或电压传感器先观察电池供给的电压的波形,再观察学生电源交流挡供给的电压的波形。这两种波形各有什么特点?”利用示波器或电压传感器呈现电池和学生电源交流挡供给的电压波形不同的情况,通过引导学生观察图像的差异,引出对交变电流和直流两种波形特点的对比讨论。
(2)交变电流
教材让学生先了解什么是交变电流,然后再学习交变电流是怎样产生的。有利于学生在感性认识的基础上再做理性分析,达到降低教学难度的效果,可以使学生更好地了解什么是交变电流,继而逐步理解、建立交变电流和直流的概念。
对于直流和交变电流的波形图问题,如果不具备用电压传感器观察直流和交变电流波形的条件,可以用示波器进行观察。由于示波器上显示的图形比较小,很多学生看不清楚,所以,最好做到两位学生使用一台示波器进行分组实验。
教学片段
观察直流和交变电流的波形图
实验电路如图 3–1 所示。
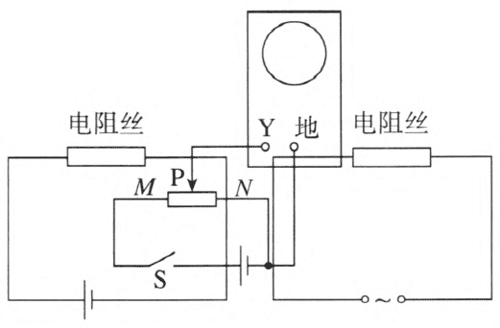
实验器材:示波器、滑动变阻器、学生电源、电池(3 V)、开关及导线。
实验操作:
①X轴扫描频率 10 ~ 100 Hz,调节扫描线成一直线并与横坐标重合。
②Y轴衰减置于“×10”挡,把“DC、AC”开关置于“DC、AC”位置。
③闭合开关 S,滑片 P 自 N 向 M 移动,可以看到扫描线为一直线且向上(如电池极性与图中相反则向下)移动。
④将图中的电池改为学生电源的交流输出,电压选择 2 V 或 3 V,把“DC、AC”开关置于“AC”位置。自 N 向 M 调节滑片 P 至适当位置,调节 Y 轴增益旋钮及 X 轴扫描频率微调旋钮,使屏幕出现 1 ~ 2 个周期的正弦波形。另外,也可以直接观察示波器内提供的 50 Hz 正弦式交变电流波形。
(3)交变电流的产生
通过以上教学片段,可以引导学生进一步思考交变电流的产生。为了加深学生对交变电流大小与方向的学习感悟,引导学生自主学习,教材让学生按发电机的旋转过程逐步分析线圈上电流的大小和方向,并把电流的大小和方向用图像的方式表达出来。这个活动要求学生能够进行发电机原理的阶段性分析,并能用定性与定量相结合的方法把电流的变化过程记录下来,从而加深学生对交变电流的认识,为后面用公式和图像确切描述交变电流的变化规律做了铺垫。
为了有利于学生理解和掌握,教材分析问题时将线圈的结构简化为便于处理的模型,也就是把磁极之间的磁场近似为匀强磁场,把 n 匝线圈等效为 1 匝线圈。为了更好地展现教材图 3.1–3 中甲、乙、丙、丁四个特殊位置,教学中要尽可能用模型或多媒体动画配合讲解。特别是要充分结合“思考与讨沦”栏目的问题,用问题串的方式引导学生分析教材图中线圈转动 1 周过程中电动势和电流的变化,并在教材图 3.1–4 中大致画出感应电流随时间变化的曲线。问题的安排设置要有一定的梯度,逐步深入,降低学习难度,突破难点。
具体设置可参考如下过程进行。
①教材图 3.1–3 中,矩形线圈转动过程中,哪些边会产生电动势?
②只有 AB、CD 边产生电动势,怎样由立体图画出平面图?注意在平面图基础上分析后续问题。
③在线圈由甲转到乙的过程中,AB 边中电流向哪个方向流动?在线圈由丙转到丁的过程中,AB 边中电流向哪个方向流动?
④当线圈转到什么位置时线圈中没有电流,转到什么位置时线圈中的电流最大?这些位置磁通量及磁通量的变化率等物理量有什么特点?
⑤大致画出通过电流表的电流随时间变化的曲线,从 E 流向 F 的电流记为正,反之为负。
在横坐标上标出线圈到达甲、乙、丙、丁各位置时对应的时刻。
在分析中注意运用电磁感应的相关知识解决新情境下的问题,以及运用数学图像对物理量随时间的变化情况进行描述。其中,用图像表示交变电流的变化规律是一种重要的方法,它形象、直观,易于被学生接受,教学中应引起重视。在教学中,要引导学生先采用描点法作图,大致画出感应电流随时间变化的曲线。需要指出的是,教材图 3.1–3 给出的是原理图,而实际的交流发电机要复杂得多。教学中应该设法突出问题的本质特征。
学生画出感应电流 i 随时间 t 变化的 i–t 图像后,大致可以猜想电流随时间变化的曲线为正弦函数图像。在前面理论分析的基础上,可以再结合示波器验证交流发电机发出的是交变电流。
教学片段
用示波器观察教学发电机发出的交流电压波形
实验装置:实验电路如图 3–2 甲所示。
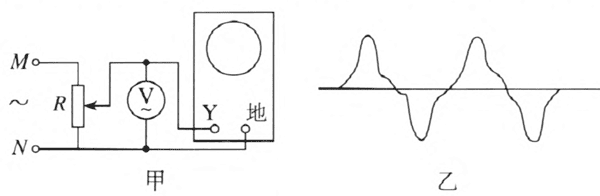
实验操作:教学发电机接在 M、N 两端(图 3–2 甲中的交流电压表可以不接)。示波器输入耦合开关置于“DC”,Y 轴衰减置于“×100”挡,X 轴扫描频率 10 ~ 100 Hz,均匀转动发电机,同时适当调节 X 轴频率微调旋钮,就可以看到发电机发出如图 3–2 乙所示的电压波形。
分析:示波器显示的电压波形呈现周期性变化的规律,表明了交变电流与直流的区别。另外,电压波形不是严格的正弦波形,其主要原因是教学发电机的磁场不是匀强磁场。
(4)交变电流的变化规律
本节学生要学习许多新名词,如交变电流、正弦式交变电流、中性面、瞬时值、峰值等。要让学生明白这些名词的准确含义。例如,交变电流从广义上讲,是方向和大小随时间做周期性变化的电动势、电压和电流的统称。对中性面的理解,要让学生明确:
①中性面是指与磁场方向垂直的平面,此时线圈中的磁通量最大;
②当线圈位于中性面时,线圈中感应电动势为 0;
③当线圈再次转过中性面时,感应电动势的方向改变。
要让学生知道,交变电流有许多种,正弦式交变电流只是其中比较基本、比较简单的一种。为什么在生产生活中使用的大多是交变电流?交变电流和直流各有什么优缺点?这些问题的提出,目的是引发学生的思考,使学生在本章的学习中始终关注交变电流的特点和有意识地在各节的具体问题中与直流对比,这不仅有助于知识的纵向联系和整体把握,还可以开阔学生思路,给学生的思维留下更大的空问。
为了继续加强学生对交变电流的认识,深度理解描述交变电流几个特征量的物理意义,教材在学生用图像大致描述感应电流随时间变化曲线的基础上,继续让学生结合图 3.1–3 分析发电机产生交变电流的过程,运用右手定则、法拉第电磁感应定律分析和推导矩形线圈在磁场中旋转时所产生的感应电动势 e、感应电流 i 和感应电压 u 随时间 t 变化的瞬时表达式。这个推导过程有一定的难度,但是具有价值。通过这个推导过程,既能让学生对发电机的模型有进一步的理解,也能让学生对发电机的发电原理和描述交变电流的特征量有更深的领悟,有助于学生学习实验观察与理论推导相结合的科学方法。
学生虽然对于观察、分析实验现象,将实际情境抽象为物理模型有一定基础,但是在涉及将立体图景转化为平面图景方面仍有困难。因此,在教学中建议对发电机产生的交变电流进行定量的分析,通过画简易交流发电机的正视图,找到几个特殊位置,明确穿过线圈的磁通量最大的位置为中性面,将线圈转动的几个特殊位置的情景图、正视图和磁通量、感应电动势、电流相互对应,理解交变电流的产生及变化规律。在进行定量分析时要注意引导学生从中性面开始计时,通过单匝闭合线圈在匀强磁场中绕垂直于磁场方向的转轴匀速转动的交流发电机模型,在正视图中应用矢量分解的方法推导出感应电动势的瞬时值随时 时间变化的表达式以及感应电动势的最大值,然后用作图的方法来描述交变电流。
教学片段
正弦式交变电流表达式的推导
提出问题:如教材图 3.1–5 所示。在磁感应强度为 B 的匀强磁扬中,矩形线圈逆时针绕中心轴匀速转动,角速度为 ω。图中标 A 的小圆圈表示教材图 3.1–3 中线圈 AB 边的横截面,图中标 D 的小圆圈表示线圈 CD 边的横截面,AB 和 CD 的长度为 l,AD 和 BC 的长度为 d,设线圈平面从中性面开始转动。则经过时间 t 后,求:
①线圈与中性面的夹角;
②AB 边的速度;
③AB 边速度方向与磁场方向的夹角;
④AB 边产生的感应电动势;
⑤线圈中感应电动势。
引导学生分析:
①线圈的角速度是 ω,经过时间 t,它与中性面的夹角 θ = ωt。
②AB 边绕中心轴做匀速圆周运动,角速度是 ω,转动半径为,所以 AB 边的速度为 \(\frac{{\omega d}}{2}\)。
③AB 边速度方向与磁场方向夹角与线圈从中性面转过的角度相同,也是 ωt。
④AB边产生的感应电动势 e1 = Blω \(\frac{d}{2}\)sinωt。
⑤线圈中感应电动势 e = 2Blω \(\frac{d}{2}\)sinωt = BωSsinωt = Emsinωt。
根据推导的函数解析式,画出正弦式交变电流的感应电动势 e、感应电流 i 和感应电压 u 时间 t 变化的图像,如教材图 3.1–6 所示。
教学中注意通过讨论影响电动势、电压、电流峰值大小的可能因素,加深对最大值以及瞬时值的理解。通过示波器演示正弦式交变电流的电流和感应电动势的瞬时值随时间变化的图像,理解交变电流的 e–t、i–t 图像。通过图像与物理情境相对应,根据交变电流的特征,学画 e–t、i–t 图像,并能从图像中读出最大值、周期等相关信息。
(5)交流发电机
交流发电机这样的应用性内容的教学,重在培养学生关注实际问题、解决实际问题的能力。在对交变电流有完整的认识后再学习交流发电机,有助于学生了解物理知识和技术、应用之间的关系,从而培养学生学以致用的能力。而了解交流发电机在实际生产生活中的应用,则能帮助学生体会物理学科在社会生产生活方面的作用和意义。
3.“练习与应用”参考答案与提示
本节共设置 4 道习题。其中第 1 题是关于对中性面特点与性质的理解,体现了物理学中的状态量、变化量、变化率之问的关系。后面 3 道计算题考查了交变电流中最大值、瞬时值的计算和关系。其中第 2 题还考查了角速度与转速的关系,而且这个关系学生在初学阶段是容易出错的。第 3 题是对交变电路中欧姆定律的考查.让学生知道欧姆定律不仅可以在直流电路中使用,而且在交变电路中也可以使用。第 4 题是一道综合性相对较强的题目,考查了学生对交变电流特点和性质的理解与掌握能力。
1.这种说法不对。根据法拉第电磁感应定律,感应电动势的大小与磁通量的变化率 \(\frac{{\Delta \Phi }}{{\Delta t}}\) 成正比,而磁通量的大小与磁通量的变化率 \(\frac{{\Delta \Phi }}{{\Delta t}}\) 没有对应关系。当线圈转到中性面位置时,穿过线圈的磁通量最大,但磁通量的变化率为 0;当线圈平面转到跟中性面位置垂直时,穿过线圈的磁通量为 0,但是磁通量的变化率最大,即感应电动势最大。从导线切割磁感线角度来看,当线圈转到中性面位置时,AB、CD 两条边都平行于磁场万向运动,没有切割磁感线,根据法拉第电磁感应定律,可知这个瞬间感应电动势为 0;当线圈平面转到跟中性面位置垂直时,AB、CD 两条边都垂直于磁场方向运动,此时线圈磁通量变化率最大,即这个瞬间感应电动势最大。
2.0.06 V
提示:当线圈平面转到与磁场平行位置时,即教材图 3.1–3 乙,感应电动势最大。线圈产生的电动势是 AB 边产生电动势的 2 倍,即 E = 2BlABω\(\frac{{{l_{BC}}}}{2}\),代入数据得 Em = 0.06 V。
3.e = 400sin(314t),0.2 A,i = 0.2sin(314t)
提示:根据题意,发电机匀速转动的线圈平面是从中性面开始计时的,感应电动势瞬时值的表达式为正弦函数 e = Emsinωt = 400sin(314t)。不计发电机线圈的内阻,电路中电流的峰值 Im = \(\frac{{{E_{\rm{m}}}}}{R}\) = 0.2 A。电流的瞬时值表达式 i = Imsinωt = 0.2sin(314t)。
4.\(\frac{{\sqrt 3 }}{2}\)BSω,电流方向为 KNML
提示:KL 边与磁场方向成 30° 时,线圈平面与中性面夹角为 60°,此时感应电动势 e = Emsinωt = BSωsin60° = \(\frac{{\sqrt 3 }}{2}\)BSω,电流方向为 KNML。
发布时间:2022/7/24 上午11:11:09 阅读次数:5132
