第九章 第六节 电容 电容器

图 9–45 上海公交 11 路超级电容车
如今在城市街头我们时常看到新能源汽车——电动汽车在路上行驶,其中超级电容车是典型的代表,作为城市公交的一员为市民提供公共服务。上海公交 11 路(图 9–45)是世界上首条使用超级电容车实现快速充电技术商业化的公交线路。
超级电容车借助车上安装的“超级电容器”,可以通过车顶的充电设备从充电站的电缆上实现几十秒的快速充电,然后继续行驶。超级电容车行驶所需的能量贮存在“超级电容器”里。
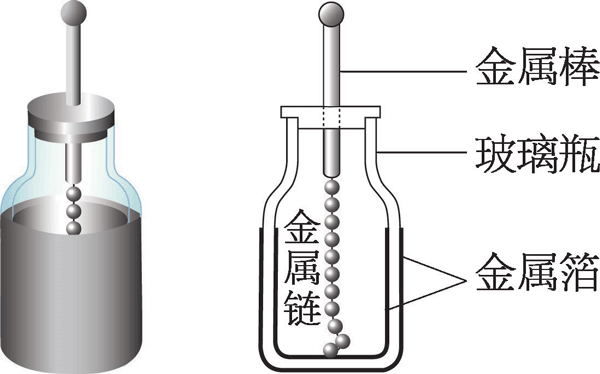
图 9–46 莱顿瓶
如图 9–46 所示的莱顿瓶可看作电容器的原型。莱顿瓶是一个玻璃容器,内外包覆着导电金属箔作为极板。瓶口插一根与外侧金属箔绝缘的金属棒,棒的上端接一个金属球,下端利用金属链与内侧金属箔连接。莱顿瓶具有贮存电荷的功能。
随着科技的发展,不断有新的用来储存电荷的装置被
创造出来,我们把能存储电荷和电能的装置叫做电容器(capacitor)。各种电容器在电子或电力设备里有广泛的应用。
电容器(图 9–47)可分为容量固定的与容量可变的两种。电容器的符号如图 9–48 所示。常见的是固定容量的电容器,包括电解电容器和瓷片电容器等。
图 9–47 常见电容器
图 9–48 电容器的符号
平行板电容器(图 9–49)是最简单的电容器。它是在两个相距很近的平行金属板中间夹上一层绝缘物质——电介质(如空气、聚丙烯、云母等)组成的。
图 9–49 电路中的平行板电容器
图 9–50 电容器的充、放电
原理图
图 9–50 中如将单刀双掷开关 S 置于接线柱 1,电源的两极就分别与电容器两极板相连接,两极板就分别带上了等量异号电荷。这个过程称为对电容器充电。每个极板所带的电荷量的绝对值叫做电容器所带的电荷量。
随着极板上积累的电荷量不断增大,电容器两极板间的电势差 U 逐渐增大。当两板间电势差增大至与电源两端电压相等时,电路中不再有电流流动,电容器的充电过程完成。此时,将单刀双掷开关 S 置于接线柱 2,电容器上的电荷中和放电,极板上电荷量下降,两极板之间的电势差 U 也随之下降。当极板上的电荷量减小为零时,两极板之间电势差也下降为零,电容器最终不再带电,电容器的放电过程完成。
充、放电是电容器的重要特性之一。它可以将电能储存起来而在需要时释放。
观察电容器的充、放电现象
实验原理与方案
如图 9–50 所示,将单刀双掷开关 S 置于接线柱 1 时就构成了电容器的充电电路。当电容器充电结束后,将开关 S 置于接线柱 2 时就构成了电容器的放电电路。
实验装置与方法
方法一:如图 9–51 所示,通过灯泡的亮度变化观察电容器的充电和放电过程。
方法二:如图 9–52 所示,利用电压传感器和电流传感器,分别代替电压表与电流表,采集所测电路的电压、电流信号,得到电容器充、放电时电压 U 和电流 I 随时间 t 变化的图像,分别如图 9–52 和图 9–53 所示;从而可了解电容器的充电和放电过程。
图 9–51 用灯泡观察电容器的充、放电电路
图 9–52 用传感器观察电容器的充、放电电路
图 9–53 U–t 图像
图 9–54 I–t 图像
实验操作和数据收集
根据方法一或方法二的实验原理图组装电路,进行实验,观察电容器的充、放电现象。
数据分析
实验观察到的现象:_______________________________________________________。
实验结论:_______________________________________________________________。
交流与讨论
电容器在充电过程中获得的能量来自哪里?
电容器在充、放电过程后,电源提供的电能又去了哪里?(电源视为其内阻为零)
将电容器 A、电压传感器、电流传感器、电压可变的直流电源等按如图 9–52 所示组成电路。调节直流电源的电压,闭合开关,分别记录电容器两极板间的电势差 U 和在不同电压下充电完毕时电容器所带的电荷量 Q(将电流传感器采集的数据处理后得到)。以电容器所带的电荷量 Q 为纵轴,以两极板间的电势差 U 为横轴,绘制电容器 A 的 Q–U 图像(图 9–55),发现电容器 A 每个极板所带的电荷量 Q 和电容器两极板间的电势差 U 成正比。
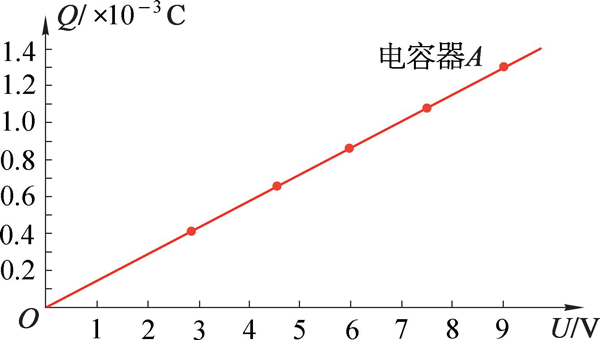
图 9–55 电容器 A 的 Q–U 图像

图 9–56 电容器 B 的 Q–U 图像
选择另一个不同的电容器 B,重复上述实验步骤,绘制电容器 B 的 Q–U 图像(图 9–56),同样发现电容器 B 每个极板所带的电荷量 Q 和电容器两极板间的电势差 U 成正比,但电容器 B 的比例系数与电容器 A 的比例系数不同。
大量研究表明,对于同一个电容器,每个极板所带的电荷量 Q 和电容器两极板间的电势差 U 成正比,也就是说 \(\frac{Q}{U}\) 是确定的;对于不同电容器 \(\frac{Q}{U}\) 一般是不同的。可见,电荷量 Q 和电势差 U 之比描述了电容器存储电荷的本领。
物理学中把电容器所带的电荷量 Q 与电容器两极板间的电势差 U 之比称为电容器的电容(capacitance),用符号 C 来表示。
\[\color{#975F85} C = \frac{Q}{U}\]
由上式可见,电容器的电容在数值上等于两极板间的电势差为 1 V 时电容器极板上所带的电荷量。电容的国际单位是法拉,简称法,用符号 F 表示。一般电容器的电容往往比 1 F 小得多,常用微法(μF)、纳法(nF)、皮法(pF)等单位,它们的关系是:
1 μF = 10−6 F,1 nF = 10−9 F,1 pF = 10−12 F
如加在电容器两极板上的电压超过某个极限数值,电介质将变成导体,这种现象称为电介质的击穿。电介质击穿导致电容器损坏。这个极限电压称为击穿电压。
电容器通常都标明电容器的电容和额定电压。额定电压是电容器长期工作时所能承受的电压,这个数值比击穿电压低。
超级电容车的“超级电容器”一般使用活性碳电极材料,具有储存电荷量大的特点,其电容可达几百至上千法。超级电容作为绿色节能的新型器件,以其容量高、寿命长、充电时间短、高效率、低污染等优异特性在交通运输、电力、机械工业等方面得到广泛的
使用。
规定电容器的电容这个物理量时采用了什么方法?在本章的学习过程中哪些物理量的定义也采用了这一方法?
示例 一个平行板电容器的电容是 0.05 μF,两极板间的电势差为 3 V,求电容器所带的电荷量。
分析:可由电容的定义公式求得电荷量。
解:已知平行板电容器的电容 C = 0.05 μF = 5×10−8 F,电容器两极板的电势差 U = 3 V。
则由电容的定义式 C = \(\frac{Q}{U}\) 得电容器的电荷量
\[\begin{array}{l}Q = CU\\ \;\;\;= 5 \times {10^{ - 8}} \times 3\;{\rm{C}}\\ \;\;\;= 1.5 \times {10^{ - 7}}\;{\rm{C}}\end{array}\]
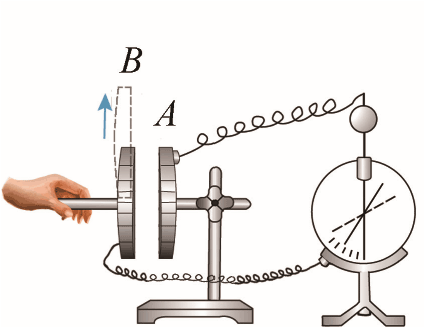
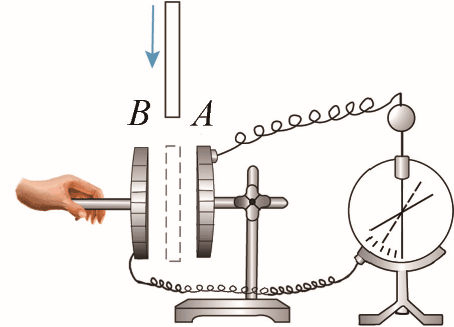
如图 9–57(a)所示,使一个极板与验电器相连的电容器充电后断开电源。在保持极板上的电荷量 Q 不变的条件下分别改变两极板的正对面积 S、两极板间的距离 d、两极板间的电介质。验电器指针的偏转角可反映两极板间电势差 U 的大小。指针偏转角大反映了两极板间电势差大,由于极板上电荷量不变,说明电容器电容值小;指针偏转角小反映了两极板间电势差小,说明电容器电容值大。因此就可用不同情况下电势差 U 的大小反映电容器电容值 C 的大小从而研究影响电容器电容的因素。
1.如图 9–57(b)所示,保持 Q、d 不变,改变 S,研究 C 与 S 的关系;
2.如图 9–57(c)所示,保持 Q、S 不变,改变 d,研究 C 与 d 的关系;
3.如图 9–57(d)所示,保持 Q、S、d 不变,在两极板间插入电介质,研究 C 与电介质的关系。

(a)
(b)
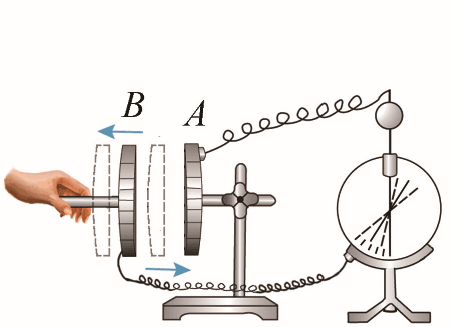
(c)
(d)
图 9–57 探究影响平行板电容器电容的因素
实验表明:S 越小,U 越大,说明 C 越小;d 越大,U 越大,说明 C 越小;插入介质板后,U 减小,说明 C 变大。
由实验可得平行板电容器的电容大小与两极板的正对面积、极板间的距离和极板间电介质有关。
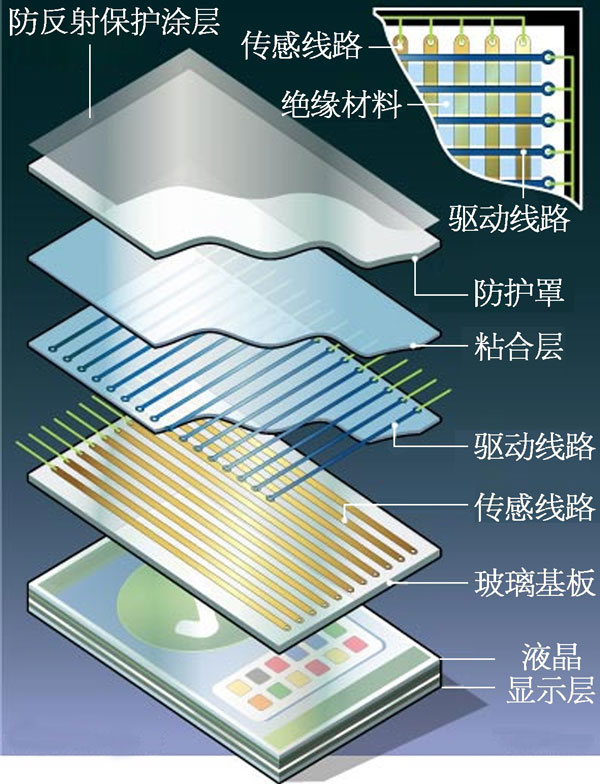
图 9–58 互电容屏结构
目前智能手机普遍采用了电容触摸屏,电容触摸屏可分为自电容屏和互电容屏两种类型。这里以支持多点触控的互电容屏为例进行说明。
如图 9–58 所示为互电容屏结构。互电容屏内部由驱动线路与玻璃基板上的传感线路等部分组成,驱动线路发出低电压高频信号投射到传感线路形成稳定的电流。
如图 9–59 所示,当手指接触到电容屏时,人体与电容屏就形成一个等效电容,而高频信号可以通过这一等效电容流入地线,这样传感线路所接收的电荷量减小,手指越靠近发射端,电荷量减小越明显,由此可根据传感线路所接收的电流确定触碰点的位置。
图 9–59 触屏原理示意图
- 如图 9–60 所示为五种不同型号的电容器,试按储存电荷本领由强到弱排序。
图 9–60
- 有一个电容器的电容为 C,当电容器所存储的电荷量 q 加倍时,其电容如何变化?如果电容器两端的电势差 U 增至三倍,其电容又如何变化?简述理由。
- 给一个额定电压为 25 V 的固定电容器充电。试在如图 9–61 所示的坐标系中画出这个电容器在充电过程中电荷量 Q、电压 U 和电容 C 这三个物理量中任意两个物理量之间的关系。
图 9–61

图 9–62


图 9–63
- 如图 9–62 所示,有一固定电容器的电容为 4.7 μF,额定电压为 50 V,求该电容器在额定电压下充电完成后所带的电荷量。若实际电压降到 40 V 时,电容器的电容和所带电荷量将如何变化?
- 手能够使手机触摸屏工作是因为手指接触到电容屏时,人体与电容屏间形成一个等效电容。普通手套一般由绝缘材料制成,戴着普通手套无法使触屏手机屏幕工作。佩戴触屏手套则可以使得触屏手机屏幕正常工作,观察如图 9–63 所示的触屏手套,触屏手套拇指和食指部位的材料有何特点,才能使手机屏幕工作?
本节编写思路
本节通过 11 路电容车引出超级电容车的快充技术能够在很短时间内储存能量,在行驶过程中慢慢释放出来,体会电容器的储能作用。
通过观察和拆解常见的电容器了解电容器的构造。通过观察电容器充、放电现象的学生实验了解电容器的作用。
利用观察不同电容器电荷量与两极板间电势差之比的实验知道用比值法来定义电容器的电容,再次体会比值定义法在定义物理量中的重要作用。
通过学生实验培养学生的实验观察能力和科学探究能力。以电容触摸屏为例来说明电容器在生活中的广泛应用,体会科学、技术、社会、环境存在相互联系,认识科学本质、培养科学态度。
正文解读
节首图所示的超级电容车仅需在公交起讫站充电数分钟,就可以完成 20 ~ 30 km 的线路运营,无需中途充电。快充高能量电容公交车由于不需要在停车场内长时间集中充电,能有效缓解中心城区停放场地紧张、供电容量不足的问题。其快充技术还可有效弥补采用慢充技术的锂电池纯电公交车在应用时充电时间较久的不足。
本节中“超级电容器”的内容与此呼应。
莱顿瓶是一种用以储存静电的装置,早期在荷兰的莱顿试用。作为原始形式的电容器,莱顿瓶曾被用来作为电学实验的供电来源,也是电学研究的重要基础器件。典型的莱顿瓶是一个玻璃容器,内外包覆着导电金属箔作为极板。瓶口上端接一个球形电极,下端利用导体(通常是金属锁链)与内侧金属箔或是水连接。莱顿瓶的充电方式是将电极接上静电产生器或起电盘等电荷源,外部金属箔接地,内部与外部的金属将会携带电荷量相等但极性相反的电荷。
建议在了解电容器的基本结构和常见的电容器时,通过观察和拆解常见的圆柱形(纸质)电容器认识电容器的外形和两个电极,拆解后观察和归纳出电容器的主要构件——两块极板和极板之间的介质,了解电容器的基本构造,突出模型建构。
电容器的分类方式可按结构分:固定电容器、可变电容器和微调电容器;按电介质分:有机介质电容器、无机介质电容器、电解电容器(符号如图 8 所示)、空气介质电容器、瓷介电容、涤纶电容、钽电容、聚丙烯电容等。
通常电容器的充、放电过程比较短暂,难以用视觉直接感受。学生在日常生活中对电容器的充、放电现象和电容器能存储和释放电荷的作用没有直观的体验,必须通过演示实验以及学生实验来观察和领会。
通过观察电容器的充、放电现象的实验,了解电容器的作用,知道电容器是一种储存电荷、储存能量的装置。
本实验应注意器材选择,宜选择电容值较大的电容器和电阻值较大的电阻(例:可选用 1 000 μF 的电容器和 200 Ω 的电阻),使得充、放电过程缓慢,容易观察(原理详见本节资料链接)。具体的实验指导可参见《普通高中教科书 物理实验与活动部分 必修》。
大容量电容器大多是电解电容,电解电容器是常用的有极性电容器。在有极性电解电容器中,两根引脚一长一短,长的为正极性,短的为负极性。无极性电解电容器的两根引脚没有正、负极之分。
实验观察到的现象:电容器的充、放电过程需要时间,电流和电压随时间变化。根据 I – t 图像可判断电容器在充、放电过程中的电流方向相反。
实验结论:在充电过程中,电流开始较大,在放电过程中,电流开始较大,随后逐渐减小到零;在充电过程中,电压开始较小,随后逐渐增大到达稳定值。在放电过程中,电流开始较大,随后逐渐减小到零;在放电过程中,电压开始较大,随后逐渐减小到零。
电容器中储存的能量来自电源提供的电能。
电源供给的电能最终转化为电路消耗的内能(忽略充、放电过程中的电磁辐射)。
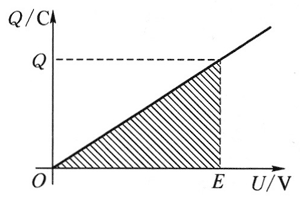
用电动势为 E 的电源给一电容为 C 的电容器充电完毕后,电容器两端的电压为 E,极板上储存的电荷量为 Q。
如图 9 所示,Q – U 图像的斜率为电容器电容 C,图像与横坐标轴围成的面积为电容器储存的电场能:W = \(\frac{1}{2}\) UQ = CU2 = CE2。这一结果可证明如下:在电容器充电的过程中,电源将总量为 Q 的正电荷由负极板输送至正极板,电源做功为 EQ。在这一过程中,电路中的电阻要消耗焦耳热,设为 A,A = \(\int {{\text{d}}A} \) = \(\int_0^Q {U{\text{d}}q} \),U 为电阻两端电压,q 为电容器极板上的电荷。由于 U = E − \(\frac{q}{C}\),得 A = \(\int_0^Q {\left( {E - \frac{q}{C}} \right){\text{d}}q} \) = EQ − \(\frac{1}{2}\frac{{{Q^2}}}{C}\) = \(\frac{1}{2}\) EQ = \(\frac{1}{2}\) CE2,即电源提供能量的一半为电阻上消耗的能量,另一半转化为电场能储存在电容器中。可见储存的能量与转化为焦耳热的能量相等。放电时,电容器储存的电场能转化为电阻上消耗的焦耳热。
此处设置“大家谈”是因为电容的定义采用了比值定义法。由此可进一步体会比值定义法在定义物理量中的重要作用。
本章学习过程中,类似的已使用比值定义法定义的物理量还有电场强度 E = \(\frac{{\mathbf{F}}}{q}\) 和电势 φ = \(\frac{{{E_{\text{p}}}}}{q}\)。
“探究影响平行板电容器电容的因素”的实验原理详见本节资料链接。
此处设置“STSE”是为了说明电容器的应用。以电容触摸屏的原理为例说明电容器在生活中的广泛应用。教学中还可以介绍电容器在照相机闪光灯电路等电子技术中的应用,体会科学、技术、社会、环境存在相互联系,认识科学本质、培养科学态度。
问题与思考解读
1.参考解答:根据电容器上标明的电容值,即可判断其储存电荷本领的强弱。因此顺序应为 e、d、c、a、b。
命题意图:认识常见的电容器,了解用电容来描述电容器储存电荷本领的强弱。
主要素养与水平:能量观念(Ⅰ);科学推理(Ⅰ)。
2.参考解答:当电容器上所存储的电荷量 q 加倍时,电容器的电容 C 不变;电容器上的电势差 U 增至三倍时,电容器的电容 C 不变。这是因为电容 C 反映的是电容器储存电荷本领的强弱,不会随外加电压的改变而改变,电容 C 与电荷量 Q 不成正比,与电压 U 不成反比。
命题意图:理解比值法定义电容的含义。电容 C 与电荷量 Q 不成正比,与电势差 U 也不成反比。这和电阻 R、电压 U、电流 I 的关系类似,R = U/I,但 R 不和 U 正正比,也不和 I 成反比。
主要素养与水平:能量观念(Ⅰ);科学推理(Ⅱ)。
3.参考解答:如图 10 所示。
命题意图:应用电容器的电荷量 Q、电压 U、电容 C 三者之间的关系解答简单的问题。
主要素养与水平:能量观念(Ⅱ);科学推理(Ⅱ)。
4.参考解答:Q = CU = 4.7 × 10−6 × 50 C = 2.35 × 10−4 C。若实际电压降到 40 V 时,电容器的电容仍为 4.7 μF,电荷量变为 Q′ = CU′ = 4.7 × 10−6 × 40 C = 1.88 × 10−4 C。电容器所带电荷量减少了 ΔQ = 4.7 × 10−5 C。
命题意图:通过计算认识电容器的电容以及电容器的充电过程。
主要素养与水平:科学推理(Ⅰ);科学论证(Ⅱ)。
5.参考解答:触屏手套在手指的部位采用了导电材料(例如含有金属的织物纤维)。因此,手指指尖与手机电容屏仍能形成等效电容,屏幕自然也就可以正常工作了。
命题意图:通过日常生活中电容触摸屏的原理,说明电容器的应用。
主要素养与水平:科学本质(Ⅰ);科学态度(Ⅱ)。
资料链接
电容器充、放电过程快慢的决定因素
对图 9 – 52 所示的电容器通过电阻的充放电过程,以 uC 及 uR 分别表示电容和电阻上的电压,当充电时开关 S 置于 1,有 uR + uC = E,uR = iR
故
\[iR + {u_C} = E\tag{1}\label{1}\]
为使上式成为只含 uC 的方程,应设法找到 i 与 uC 的关系。i 是单位时间内流进电容器极板的电荷量,即 i = \(\frac{{{ \text{d}}q}}{{{\text{d}}t}}\),它与 uC 又有如下关系:q = CuC
故
\[i = C\frac{{{\text{d}}{u_C }}}{{{ \text{d}}t}}\tag{2}\label{2}\]
将 ② 代入 ① 式得
\[RC\frac{{{\text{d}}{u_C }}}{{{ \text{d}}t}} + {u_C} = E\tag{3}\label{3}\]
这便是 uC(t) 所满足的微分方程,其通解为
\[{u_C}(t) = E + A{e^{ - \frac{t}{{RC }}}}\tag{4}\label{4}\]
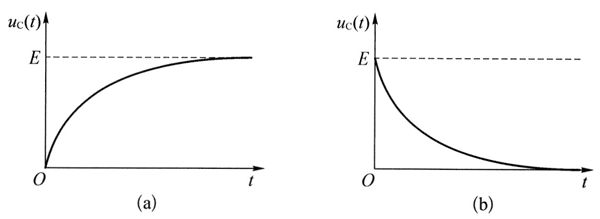
令开关闭合时刻为 t = 0,则初始条件为 uC(0) = 0,代入通解 ④ 式可得:A = − E,故得特解 uC(t) = E(1 − \({e^{ - \frac{t}{{RC}}}}\)),t ≥ 0。uC 的曲线如图 11(a)所示,可知 uC 以指数方式随 t 增大,最后达到稳定值 E。电源通过电阻对电容的充电过程的快慢取决于 RC 乘积,我们称它为 RC 电路的时间常数。即
对电容器充电完成后通过电阻的放电过程,开关 S 置于 2。电容器通过电阻放电,则有 uR + uC = 0
即
\[iR + {u_C} = 0\tag{5}\label{5}\]
将 ② 代入 ⑤ 式得
\[RC\frac{{{\text{d}}{u_C}}}{{{ \text{d}}t}} + {u_C} = 0\tag{6}\label{6}\]
其通解为
\[{u_C}(t) = A{e^{ - \frac{t}{{RC }}}}\tag{7}\label{7}\]
因开关改置 2 前 uC = E,根据 uC 不能突变的原则,可得初始条件为 uC(0) = E,代入通解 ⑦ 式可得:A = E,故得特解 uC(t) = E \({e^{ - \frac{t}{{RC}}}}\)。由此,放电时 uC 随时间变化如图 11(b)所示,可知 uC 以指数方式随时间下降为零,下降的快慢同样取决于时间常数 RC。
电容器“隔直流、通交流”的含义
电容对直流电有“隔直流”作用,是指在直流电流对电容器充电完成后,电路中就没有电流了。在直流电源刚加到电容器上时,电路中是有电流流动的,这一电流是对电容器的充电电流。这一电流流动的过程很快就会结束,具体时间长短与电路中电阻和电容的大小有关,两者的乘积越大充电时间就越长,反之越短,而且电流并不通过电容器。充电完成后,电容器两端的电压等于直流电源电压的大小。在交流电的一个周期内,由于对电容器的正反向充电,流过电路中的电流方向是改变的,但对电容器反复充、放电,就会使电路中始终有电流通过,此时虽然电流仍不通过电容器,但可以等效地视为电容器并未阻隔电流,即电容器能够让交流电“通过”电路,这就是电容器的“通交流”特性。通常电容器的两个极板之间都填充以绝缘介质.所以不会通过自由电荷,即电流不能“穿”过电容器。我们所说的“通交流”,其实是靠电容器两端不断充电和放电的过程形成的。此时,电容器的外部线路中有电流通过,内部仍然无电流通过。
纯电容电路的电流和电压的相位关系
电容器的充放电电流 i 等于电容器极板电荷量 q 的变化率,即 i = \(\frac{{{ \text{d}}q}}{{{\text{d}}t}}\)。极板电荷量q 与 u 的关系为 q = Cu,可得
\[i = C\frac{{{\text{d}}u}}{{{\text{d}}t}}\tag{1}\label{8}\]
如果对电容器施加简谐函数式的交变电压 u,可写成
\[u = {U_m}\cos (\omega t + {\varphi _u}) = \sqrt 2 U\cos (\omega t + {\varphi _u})\tag{2}\label{9}\]
将 ② 代入 ① 式得
\[i = \sqrt 2 \omega CU\cos (\omega t + {\varphi _u} + \frac{\pi }{2})\tag{3}\label{10}\]
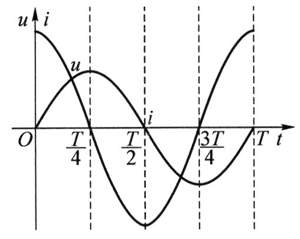
纯电容电路电流的初相等于 φi = φu + \(\frac{\pi }{2}\) 或 φi – φu = \(\frac{\pi }{2}\)。电容器在交流电路中的这种特性可表述为:纯电容电路的电流相位比电压相位超前 \(\frac{\pi }{2}\),如图 12 所示。
平行板电容器的电容表达式
当平行板电容器的两极板间是真空时,电容 C 与极板面积 S、极板间的距离 d 的关系为:C = \(\frac{S}{{4\pi kd}}\),式中 k 为静电力常量。
当两极板之间充满同一种介质时,电容 C = \(\frac{{{\varepsilon _{\text{r }}}S}}{{4\pi kd}}\),式中 εr 是一个常数,与电介质有关,称为电介质的相对介电常数。
“拓展视野”中“探究影响平行板电容器电容的因素”的实验原理
验电器在此实验中也构成一个电容器。已充电的平行板电容器与验电器相连就构成两个电容器并联,设平行板电容器的电容为 C1,验电器的电容为 C2。因为平行板电容器的两个极板上分别带有等量的异号电荷,这样它必然对验电器充电。充电的结果使平行板电容器的电荷量为 Q1,验电器的电荷量为 Q2,两并联电容处于充电平衡状态,即两个电容器两极的电势差相等,均为 U。则它们的总电荷量为 Q = Q1 + Q2 = C1U + C2U。由于验电器的结构设计,它的电容 C2 非常小只能容纳很少的电荷,验电器上电荷量的变化对平行板电容器而言总是可以忽略不计的,因此,平行板电容器的电荷量可以认为就是总的电荷量即 Q = C1U。验电器的偏转角和其上的电荷量正相关,验电器的电容不变,则验电器的电荷量与验电器自身电容上的电势差成比例,此电势差即所研究的乎行板电容器的电势差。即教材中所述“验电器指针的偏转可反映两极极板间电势差 U 的大小”的原因。
保持极板上电荷量 Q 不变的情况下,如验电器的指针偏转角大,说明平行板电容器的电势差 U 大,由 C1 = \(\frac{Q}{U}\),可知平行板电容器的电容值 C1 小。反之,如验电器的指针偏转角小,说明平行板电容器的电势差 U 小,可知平行板电容器的电容值 C1 大。
发布时间:2022/5/20 上午10:36:44 阅读次数:8503

