如何认识电容器电容与孤立导体的电容？

中学物理教科书中讲的是电容器的电容，它定义为电容器某一极板上的电荷 Q 与两极板间的电压 U 的比值，即电容 C = \(\frac{Q}{U}\)。任何两个相互绝缘的导体都可以组成一个电容器，而所谓孤立导体，指的是一个导体离其他导体都足够远，或者说其他导体对它的影响可以忽略的情况。最简单的电容器是平行板电容器，最简单的孤立导体是孤立的导体球，地球就可以近似看作孤立导体球。

中学教科书中讲的电容是电容器的电容。两个相互绝缘的导体组成一个电容器；单独一个导体，就称为孤立导体，它也有电容。电容器电容与孤立导体的电容之间是怎样的关系呢？

一、电容器电容

最简单的电容器是平行板电容器，它由两块相距很近且相互绝缘的平行金属板构成，这两个导体称为电容器的两个极板，两极板之间可以是真空，也可以存在介质，在不要求很精确的情况下，空气可以近似认为是真空。任何两个距离很近而又绝缘的导体，都可以看成一个电容器。把电容器的两个极板分别与电源的两极相连，如果其申的一个极板带正电荷，电荷量为 Q，另一个极板一定带上数量相等的负电荷，并且两极板间产生电势差 U，我们把其中一个极板上所带的电荷量 Q 称为电容器的电荷量，电容器所带的电荷量 Q 与电容器两极板间的电势差 U 的比值，叫作电容器的电容。用 C 表示电容，则有 C = \(\frac{Q}{U}\)。

电容器的电容在数值上等于使电容器两极板间电势差为 1 V 时所带的电荷量，或者说等于使两极板间电压升高 1 V 所需要增加的电荷量。

最简单的平行板电容器，其电容 C 与两极板的正对面积 S 成正比、与两极板间的距离 d 成反比，与充满极板间电介质的介电常数 ε 成正比，即 C = \(\frac{{\varepsilon S}}{{kd}}\)，式中 k 就是静电力常量，在国际单位制中，k = 9.0×10⁹ N·m²/C²。

其他电容器都可以看作平行板电容器的变形，决定其电容的公式也不尽相同，但“两极板的正对面积”“两极板间的距离”以及“板间电介质的介电常数”都是影响其电容大小的因素。

二、孤立导体的电容

一个导体，如果附近没有其他导体或带电体，就说它是孤立导体。真正严格的孤立导体实际上是不存在的，但只要其他导体或带电体距离它足够远，就可以将其看作孤立导体。某孤立导体的电荷量为 q，它具有一定的电势 φ，电荷量 q 与它的电势 φ 的比值，称为该孤立导体的电容，用 C 表示电容，则有 C = \(\frac{q}{\varphi }\)。

孤立导体电容的定义式 C = \(\frac{q}{\varphi }\) 与电容器电容的定义式 C = \(\frac{Q}{U}\) 形式上相近，但有一个显著的不同，即孤立导体的电势 φ 的数值与电势零点的选取有关，对于点电荷或者孤立的带电导体球一般都以无穷远处为电势零点，而两导体间的电势差 U 则与电势零点的选取无关。

其实孤立导体与电容器并不是完全不相干的，构成一个电容器的两个导体如果相距很远，远到它们间的相互影响可以忽略，就可以看成两个孤立导体，因此可以说孤立导体就是电容器的一种特殊情况，即它与无穷远处另外的孤立导体组成电容器。由于两个孤立导体间的距离很大，因此孤立导体的电容一般都很小，而写另一个相距较近的导体组成电容器，电容就会变大。

最简单的孤立导体是球形，设其半径为 R，带电荷量为 q，由于是孤立导体，不受其他电场影响，它的电荷均匀分布在外表面，可以将其看作集中于球心处的点电荷，以无穷远处为电势零点，则球面处的电势 φ = k \(\frac{q}{R}\)，而导体球是一个等势体，因此它也是导体球的电势，则它的电容 C = \(\frac{q}{\varphi }\) = \(\frac{R}{k}\)。

一般的球形导体，作为孤立导体，其电容是很小的，如图 1 所示，为实验室常用的绝缘导体球，设其半径为 0.1 m，则它的电容

\[C = \frac{{{{10}^{ - 1}}}}{{9 \times {{10}^9}}}\;{\rm{F}} \approx {10^{ - 11}}\;{\rm{F}} = 10\;{\rm{pF}}\]

地球是一个庞然大物，其半径 R = 6.4×10⁶ m，如果把它看作一个孤立的导体球，它的电容 C = \(\frac{R}{k}\) = 7.1×10⁻⁴ F。

三、研究平行板电容器的电容与哪些因素有关的实验为什么只能是定性的？

研究平行板电容器的电容与哪些因素有关的实验装置如图 2（a）所示，把平行板电容器的 A 板与静电计的金属小球相连接，把平行板电容器的 B 板及静电计的金属外壳都接地，或者如图 2（b）所示直接把平行板电容器的 B 板与静电计的金属外壳相连接。用带电物体接触 A 板使它带电，静电计的指针张开一定角度，可以保持 A、B 两板间的距离一定而改变二者的正对面积，也可以保持 A、B 两板间的正对面积一定而改变二者的距离，还可以保持 A、B 两板间的正对面积及距离都不变，而在两板间插入不同的介质，由此观察静电计指针偏转角度的变化，就可以定性地得出平行板电容器的电容 C 跟两极板的正对面积 S 正相关、跟两极板间的距离 d 负相关，且与两板间的介质有关，但得不出成正比或反比的结论。

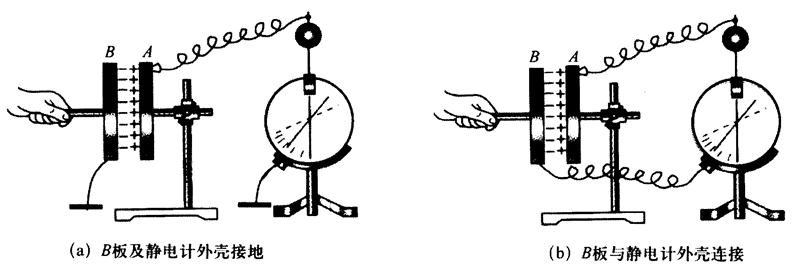
为什么说该实验只能定性地研究平行板电容器的电容跟哪些因素有关，却不能得出定量的结论呢？这要从静电计本身讲起。静电计又叫电势差计或指针验电器，是一种半定量的测量仪器，它的外壳前面是透明的玻璃，便于观察，后面毛玻璃盘面上刻有刻度，而侧面是金属外壳，外壳的中央有一个绝缘塞，塞中间穿有一根金属杆，杆的上端连接着金属小球、下面安有可转动的金属指针。中央的金属导体（金属杆及金属指针）与边缘的金属外壳组成一个电容器，使用比较精密的万用电桥可以测量它的电容值，中学实验室使用的静电计的电容大约 7 ~ 9 pF。

静电计使用时金属外壳可以接地，也可以不接地。当中央的金属杆与指针带电时，例如带有正电时，如果金属外壳接地，则外壳的内壁将由于静电感应而带上负电，外壁则不带电。金属指针的张角反映的是中央导体与金属外壳间的电势差。

图 2（a）把 B 板与金属外壳都接地，当 A 板带上正电时，B 板的右侧与金属外壳的内侧都会由于感应而带上负电，而 B 板的左侧与金属外壳的外侧都不带电；图 2（b）用导线把 B 板与金属外壳连接起来而不接地，当 A 板带上正电时，B 板的右侧与金属外壳的内侧都会由于感应而带上负电，而 B 板的左侧与金属外壳的外侧则带上等量的正电荷。

这两种连接方法的实质都是两个电容器的并联，一个电容器是平行板电容器，另一个电容器则是静电计本身。长期以来，在中学物理教学中，都把这个实验说成是在保持平行板电容器带电荷量 Q 不变的情况下，探究它的电容与哪些因素有关，但这并不准确！由于是两个电容器并联，当我们使 A 板带上一定量的电荷 Q，并且改变 A、B 两极板的正对面积，或改变板间距离、板间介质，保持不变的是两个电容器所带的总电荷量，而不是平行板电容器的带电荷量。

设平行板电容器的电容为 C₁，带电荷量为 Q₁，静电计的电容为 C₂，带电荷量为 Q₂，由于两电容器并联，电压相等，则有

\[\frac{{{Q_1}}}{{{C_1}}} = \frac{{{Q_2}}}{{{C_2}}}\]

又由于 Q₁ + Q₂ = Q，可得 Q₁ = \(\frac{{{C_1}}}{{{C_1} + {C_2}}}\)Q。

在实验过程中，C₂ 可认为保持不变（严格地讲，随着静电计指针偏转角度的改变，其电容 C₂ 也会有变化，但变化量不大），而 C₁ 在不断变化，其带电荷量 Q₁ 必然要发生变化。只有在 C₂ 相比 C₁ 小很多的情况下，Q₁ 才可以近似认为保持不变。但实际情况并不满足这样的条件，我们使用的平行板电容器的直径约为 20 cm，即半径 R = 10⁻¹ m，面积 S = πR²，当两板正对且间距等于 d = 5 cm = 5×10⁻² m 时，其电容

\[{C_1} = \frac{S}{{4\pi kd}} = \frac{{\pi {R^2}}}{{4\pi kd}} = \frac{{{R^2}}}{{4kd}} = \frac{{{{10}^{ - 2}}}}{{4 \times 9 \times {{10}^9} \times 5 \times {{10}^{ - 2}}}}\;{\rm{F}} = 5.6 \times {10^{ - 12}}\;{\rm{F}} = 5.6\;{\rm{pF}}\]

即 C₁ 与 C₂ 电容的数量级相同，C₂ 的影响不能忽略，即不能认为平行板电容器的带电荷量 Q₁ 保持不变。

关于静电计指针张角的变化，可以这样解释：由于电容器 C₁ 与 C₂ 并联，在总电荷量保持不变的条件下，两电容器各自所带的电荷量跟它们的电容成反比，现在 C₂ 可以认为保持不变，而当 C₁ 减小时（减小 C₁ 的正对面积 S，或增大两板间距离 d），部分电荷向静电计（C₂）转移，静电计金属杆和指针所带的电荷增多了，因此指针张角变大。也可以这样解释：由于电容器 C₁ 与 C₂ 并联，可以用一个等效的电容 C（C = C₁ + C₂）代替它们，两电容器的总电荷量保持不变，即等效电容 C 的带电荷量保持不变，当 C₁ 减小时（减小 C₁ 的正对面积 S，或增大两板间距离 d），电容 C 也随之减小，而电荷量 Q 保持不变，因此电势差 U 变大，从而静电计指针张角变大。

发布时间：2024/8/12 上午9:02:19  阅读次数：1332