第五章 第三节 带电粒子在匀强磁场中的圆周运动

 

 

 

我们已经知道运动电荷所受的洛伦兹力与速度方向垂直，那么带电粒子在洛伦兹力的作用下，在磁场中会如何运动呢？现在我们来更详细地研究磁场中带电粒子的运动。

如图 5–29 所示是洛伦兹力演示仪。由电子枪产生电子束，玻璃泡内充有稀薄气体，当电子通过时能够显示电子的径迹。玻璃泡前后各有一个励磁线圈，它们能够在两线圈之间产生与两线圈中心的连线平行的匀强磁场。电子的速度大小可以通过电子枪的加速电压调节，匀强磁场的磁感应强度则可以通过励磁线圈的电流调节。

图 5–29 洛伦兹力演示仪

 

在图 5–30（a）中，洛伦兹力演示仪没有加磁场，向左射出的电子束的运动径迹是一条直线；在图 5–30（b）中，通过给洛伦兹力演示仪的两励磁线圈通电，产生沿两线圈中心连线方向的匀强磁场，向左射出的电子束在匀强磁场中的运动径迹是一个圆。

我们只讨论最简单的情况，带电粒子垂直射入匀强磁场。根据左手定则，洛伦兹力跟粒子运动的速度方向垂直，使带电粒子的运动方向发生偏转。因为洛伦兹力始终跟粒子的速度方向垂直，所以，洛伦兹力只改变粒子运动的方向，而不改变速度大小。由洛伦兹力公式 f = qvB 可知，因为 q、v 和 B 都不变，洛伦兹力的大小也不变。

在学习圆周运动时我们就知道，如果作用在质点上的力大小不变，方向始终与质点运动速度方向垂直并且指向圆心，这个质点一定做匀速圆周运动。现在是洛伦兹力作用在带电粒子上，带电粒子做匀速圆周运动，洛伦兹力就是带电粒子做匀速圆周运动的向心力。所以，沿着与磁场垂直方向射入匀强磁场的带电粒子应做匀速圆周运动，如图 5–31 所示。

不仅如此，由于洛伦兹力始终与带电粒子的速度方向垂直，它不可能改变带电粒子速度的大小，也就不可能对带电粒子做功，带电粒子的动能不会改变。

我们观察到出射电子的速率 v 不变时，磁感应强度 B 越大，电子束做圆周运动的半径 r 越小；保持磁感应强度 B 不变时，出射电子的速率 v 越大，电子束做圆周运动的半径 r 越大。

假设一个质量为 m、电荷量为 q 的带电粒子，在磁感应强度为 B 的匀强磁场中做速度大小为 v、半径为 r 的匀速圆周运动。

 

粒子做匀速圆周运动所需的向心力 F = m \(\frac{{{v^2}}}{r}\)，这就是磁场作用在带电粒子上的洛伦兹力 f = qvB。所以

\[qvB = m\frac{{{v^2}}}{r}\]

由此得出

\[\color{#945E55}r = \frac{{mv}}{{qB}}\]

上式表明，在匀强磁场中的带电粒子，在洛伦兹力的作用下做匀速圆周运动的轨道半径与粒子的速度、质量、电荷量和磁感应强度都有关。对于给定的粒子，\(\frac{q}{m}\) 是一确定的值，如果 B 也是确定的，则 r ∝ v，即轨道半径与粒子的速率 v 成正比；如果 v 是确定的，则 r ∝ \(\frac{1}{B}\)，即轨道半径 r 与磁感应强度 B 成反比。

根据带电粒子做匀速圆周运动的周期 T = \(\frac{{2\pi r}}{v}\)，将 r = \(\frac{{mv}}{{qB}}\) 代入，得到

\[\color{#945E55}T = \frac{{2\pi m}}{{qB}}\]

由此可见，带电粒子在磁场中做匀速圆周运动的周期跟轨道半径 r 及速率 v 无关，只与粒子的质量 m、电荷量 q 和磁场的磁感应强度 B 有关。

 

示例 一个初速度为零的质子，经过电压 U = 1.3×10³ V 的电场加速后垂直进入磁感应强度 B 为 0.20 T 的匀强磁场。质子的质量 m = 1.67×10⁻²⁷ kg， 电荷量 q = 1.6×10⁻¹⁹ C。求：

（1）质子进入磁场时的速度大小；

（2）质子在磁场中运动的轨道半径；

（3）质子做匀速圆周运动的周期。

分析：电场可以使带电粒子加速，也可以使它偏转；带电粒子垂直进入磁场只能使带电粒子偏转。本题中质子受电场加速，然后在匀强磁场中做匀速圆周运动。

解：（1）初速度为零的质子在电场中被加速，获得动能。质子在电场中得到的动能等于电场对它所做的功，设质子进入磁场时的速度大小为 v，则有

 

\[\frac{1}{2}m{v^2} = qU\]

所以                                                              \(\begin{array}{l}v = \sqrt {\frac{{2qU}}{m}} \\ = \sqrt {\frac{{2 \times 1.6 \times {{10}^{ - 19}} \times 1.3 \times {{10}^3}}}{{1.67 \times {{10}^{ - 27}}}}} \;{\rm{m/s}}\end{array}\)

                                                                      ≈ 5.0×10⁵ m/s

（2）质子垂直射入匀强磁场，做匀速圆周运动。设质子做匀速圆周运动的半径为 r，它在磁场中受到的洛伦兹力提供质子做匀速圆周运动所需的向心力，得

\[qvB = m\frac{{{v^2}}}{r}\]

所以，质子在磁场中运动的轨道半径

\[\begin{array}{l}r = \frac{{mv}}{{qB}}\\ = \frac{{1.67 \times {{10}^{ - 27}} \times 5 \times {{10}^5}}}{{1.6 \times {{10}^{ - 19}} \times 0.20}}\;{\rm{m}}\end{array}\]

                                                             ≈ 2.6×10⁻² m

（3）质子做匀速圆周运动的周期

\[\begin{array}{l}T = \frac{{2\pi r}}{v}\\ = \frac{{2 \times 3.14 \times 2.6 \times {{10}^{ - 2}}}}{{5 \times {{10}^5}}}\;{\rm{s}}\end{array}\]

                                                            ≈ 3.3×10⁻⁷ m

 

 

洛伦兹力在生产、生活中也有着很广泛的应用，比如质谱仪、电子显微镜、回旋加速器、磁流体发电机等。

洛伦兹力在现代科学技术中有很多的应用，我们通过如下几个实例来说明。

1．质谱仪

我们知道，微观粒子的质量都很小，体积也很小。那么怎样测定单个粒子的质量呢？利用洛伦兹力设计的质谱仪就能完成这一任务。

质谱仪结构如图 5–33 所示，P 为一带电粒子源，产生正离子；正离子经 S₁ 和 S₂ 之间高电压加速后，进入专门设计的速度选择器。速度选择器的作用是使正离子在经过电场和磁场共同存在的空间后（速度选择器中的电场强度为 E，磁感应强度为 B，电场方向与磁场方向相互垂直），只有所受洛伦兹力和电场力二力平衡的那些正离子，才能以一定速率 v 从 S₃ 缝射出并进入磁场 B₀，即

\[qE = qvB\]

由此得出

\[v = \frac{E}{B}\]

S₃ 下方有一垂直纸面向外的匀强磁场，磁感应强度为 B₀。正离子在磁场中只受始终与速度方向垂直的洛伦兹力的作用，粒子在洛伦兹力作用下沿半圆轨迹运动并被质谱仪记录底片收集。

由速度选择器选出的速率 v =  \(\frac{E}{B}\) 和轨道半径 r = \(\frac{{mv}}{{q{B_0}}}\)，可得出圆周运动轨道半径 r 与带电粒子的质量 m 之间的关系式

\[r = \frac{{mE}}{{q{B_0}B}}\]

由此得出带电粒子的质量 m 与质谱仪底片上谱线到 S₃ 缝间的距离 X 之间的关系式

\[m = \frac{{q{B_0}Br}}{E} = \frac{{q{B_0}BX}}{{2E}}\]

式中 B₀、B、E 均为定值。

可见如果粒子的电荷量 q 相同，由质谱仪底片上谱线到缝之间的距离 X 即可确定粒子的质量 m。这样，不同质量的粒子打在质谱仪底片上的位置就按质量大小的顺序排列，类似于光谱按波长排列，所以把上述仪器叫做质谱仪。

 

 

质谱仪最初是由英国科学家阿斯顿设计的，后来经过多次改进，现已成为测量带电粒子的质量和分析同位素的重要工具。

2．回旋加速器

当我们研究原子核的结构时，往往需要用高能量的微观粒子去轰击原子核进行研究。如何得到能量很高的粒子呢？我们可以想到用加速电场对带电粒子加速。理论分析表明，只要加速电场足够强，加速距离足够长，就可以使带电粒子获得足够高的能量。这样的装置叫做直线加速器。但是在技术上电场强度是不可能无限制地增大的，在真空中的加速距离也有一定限制，建造数千米长的直线加速器已很困难。能不能把带电粒子限制在一定的空间范围内同时又能对它不断加速呢？回旋加速器就可以完成这个任务。

如图 5–34 所示，回旋加速器的核心部分 D₁ 和 D₂ 是两个中空的半圆金属盒，它们之间有一定的电势差；粒子源 G 产生的带电粒子在两盒之间被电场加速；两个半圆盒处于与盒面垂直的匀强磁场中，粒子在半圆盒内受磁场洛伦兹力的作用做匀速圆周运动。经过半个圆周之后，到达两盒间的缝隙时，控制两盒间的电势差，使其恰好改变正负，于是粒子经过盒缝时再一次被加速。如此，粒子在做圆周运动的过程中一次一次地经过盒缝，而两盒间的电势差一次一次地反向，粒子在间隙内总被加速，从而使其沿螺线轨迹逐渐趋近于盒的边缘。达到预期的速率后，用特殊装置把它们引出。

如图 5–35 所示为中国原子能科学研究院自主研发的 100 MeV 质子回旋加速器。此回旋加速器可以调试出速度接近一半光速的质子束，这标志着我国回旋加速器达到国际同类装置的先进水平。现在回旋加速器已经获得广泛应用，例如可生产治疗癌症的同位素药物。作为放射线源，我国制造的紧凑型回旋加速器已在各地的医院里普遍使用。

 

本节编写思路

本节以洛伦兹力演示实验作为情境，该实验能清晰地演示没有磁场时带电粒子的运动轨迹为直线，加磁场后带电粒子的运动轨迹为一个圆周。首先形象地显示带电粒子在匀强磁场中的圆周运动，然后理论探究带电粒子做圆周运动的原因，自主推导圆周运动的半径和周期，体现从具体到抽象的认识过程。

通过介绍质谱仪和回旋加速器的工作原理，了解直线加速器和回旋加速器面临的技术难题，体会科学与技术之间的密切关系。

通过本节学习，有助于进一步提升学生关于电磁场的物质观念和能量观念。经历带电粒子在匀强磁场中的圆周运动的学习，感受实验观察和数学推导等研究物理的基本方法。认识质谱仪利用电场、磁场控制带电粒子的运动，从而能区分同位素的原因，提高模型建构和科学论证的能力。

正文解读

励磁线圈（此处也叫亥姆霍兹线圈）的“励磁”就是激发产生磁场，此处励磁线圈是一对彼此平行的共轴串联的圆形线圈。圆形线圈产生的磁场的磁感应强度沿中轴线分布较均匀。如图 8 所示，励磁线圈能够在两线圈之间近似产生与两线圈中心的连线平行的匀强磁场。

 

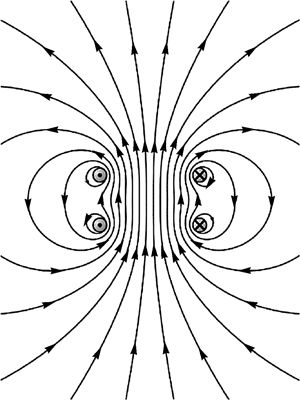
本自主活动是演示实验，目的是显示如带电粒子垂直入射匀强磁场，会在匀强磁场中做匀速圆周运动。

 

本自主活动是演示实验，目的是：

（1）知道在匀强磁场中影响带电粒子圆周运动半径大小的因素。

（2）验证带电粒子在匀强磁场中做匀速圆周运动的半径与磁感应强度的大小和电子的速率有关，体会理论必须经过实验检验的科学研究环节。

为了使学生能计算匀速圆周运动的周期和半径，先通过自主活动分别改变磁感应强度 B 和出射电子的速率 v，观察电子圆周运动半径 r 发生变化。再进行理论探究，洛伦兹力提供了带电粒子做匀速圆周运动所需的向心力。

 

建议让学生自主推导带电粒子在匀强磁场中做匀速圆周运动的半径和周期，既巩固前面学习的知识，也能弄清各个物理量之间的关系。

 

带电粒子在匀强磁场中做匀速圆周运动的频率为

f = \(\frac{1}{T}\) = \(\frac{{qB}}{{2\pi m}}\)

频率 f 是带电粒子在磁场中运动的特征频率，也叫作回旋频率。

 

此处设置“大家谈”是为了比较电场和磁场对带电粒子的作用的差异。电场力和磁场力都能使带电粒子偏转，但却是两种性质不同的力。电场力和磁场力差异如下表所示。

 

力的名称	电场力（库仑力）	磁场力（洛伦兹力）
作用对象	静止或运动电荷	运动电荷
力的大小	fE = qE 与电荷运动速度无关	fB = qvB 与电荷运动速度有关
力的方向	与电场 E 平行； 正电荷受到的电场力与 E 方向相同，负电荷受的电场力与 E 方向相反	与速度 v 和磁场 B 所确定的平面垂直；先要区别正、负电荷，再用左手定则判断
作用效果	改变电荷的速度大小和方向； 可对运动电荷做功； 可改变电荷动能	只改变电荷的速度方向，不改变速度大小； 不能对运动电荷做功； 电荷动能不变

 

此处设置“拓展视野”，是为了介绍带电粒子在匀强磁场中运动的一般情况。（详见本节资料链接）

 

磁流体发电技术（详见本节资料链接）

 

质谱仪是分离和检测不同同位素的仪器。仪器的主要装置放在真空中。将物质气化、电离成带电粒子束，带电粒子通过电场和磁场的加速，选择和偏转后打到质谱仪底片上的不同位置，从而获得不同同位素的质量谱。质谱仪最重要的应用是分离同位素并测定它们的原子质量及相对丰度（同位素丰度比）。测定原子质量的精度超过化学测量方法，大约 \(\frac{2}{3}\) 以上的原子的精确质量是用质谱方法测定的。由于质量和能量的当量关系，由此可得到有关核结构与核结合能的信息。用于矿石中提取的放射性衰变产物（元素）的分析测量可确定矿石的地质年代。质谱方法还可用于有机化学分析，特别是微量杂质分析和测量分子的分子量，为确定化合物的分子式和分子结构提供可靠的依据。由于化合物有着像指纹一样的独特质谱，质谱仪在工业生产中也得到广泛应用。

 

此处设置“大家谈”，是为了引导学生进一步理解质谱仪的原理与作用。同位素的电荷量相同，质量不同，即荷质比（带电粒子的电荷量和其质量的比值）不同。荷质比不同的同位素经同一速度选择器后进入磁场时的速率相同，进入磁场后圆周运动的轨道半径与粒子质量成正比，打到质谱仪底片上的位置因此不同。由质谱仪底片上谱线的位置即可确定粒子的质量。

 

要加大直线加速器的加速距离，一个办法就是把加速电场“卷起来”。利用磁场改变带电粒子的运动轨迹，让粒子转圈式地多级加速，这就引入了回旋加速器。回旋加速器是“粒子加速器”的一种。由于粒子每次经过电场时必须被加速，所以粒子每运动半个周期，电场都必须改变方向。随着带电粒子在磁场中被多级加速，带电粒子的速率越来越大。回旋加速器所依据的基本原理就是带电粒子垂直于匀强磁场做匀速率圆周运动时周期 T = \(\frac{{2\pi m}}{{qB}}\) 与速率无关。随着带电粒子的速率逐步增大，其轨道半径也越来越大，但绕过半个圆周所用的时间是不变的，都等于回旋周期的一半即 \(\frac{T}{2}\) = \(\frac{{\pi m}}{{qB}}\)，因此每经过半个圆圈之后使电场方向反向，就能确保粒子经过缝隙时都能得到加速。

 

当质子的能量高于 50 MeV 时，常规的回旋加速器开始失效，因为其设计假设之一是在磁场中作圆周运动的带电粒子的周期与速率无关。但由于相对论效应，随着质子的速率增加，质子的回转周期将随速度增加，因而质子圆周运动的周期与回旋加速器交变电场的周期不再同步，从而限制质子能量的增加。另一个困难是传统的回旋加速器的磁场由大型电磁铁提供，要增大 D 型盒半径，电磁铁的面积却不可能无限增大。质子同步回旋加速器的设计与制造就是克服这两个困难的。均匀磁场的磁感应强度 B 和加速电场的周期不再像传统的回旋加速器那样是固定的值，而是在加速循环时随时间变化，使之与粒子回旋运动保持同步，质子沿一个圆形而不是螺旋形轨道运动。

 

此处设置“拓展视野”，不仅仅是介绍磁场在现代科学技术中的应用，更重要的是通过阿尔法磁谱仪 2 的“中国心”和暗物质粒子探测卫星的成功发射和在轨运行，展现我国在近代科技方面取得的成就。在暗物质探测领域取得重大突破，对促进我国空间科学领域的创新发展具有重大意义，从而激发学生的学习积极性和探究欲望，促进学生物理学科核心素养的全面发展。

问题与思考解读

1．参考解答：电子顺时针运动。运动电荷在磁场中受到的洛伦兹力提供电子做匀速圆周运动的向心力，指向圆心。由左手定则可判断正电荷应逆时针转动，从而可得电子顺时针运动。

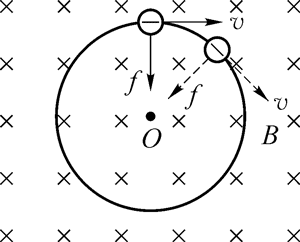
图 9

命题意图：引导学生判断洛伦兹力与电荷运动之间的关系。

主要素养与水平：运动与相互作用观念（Ⅱ）；科学推理（Ⅱ）。

 

2．参考解答：带电粒子在匀强磁场中做匀速圆周运动 qvB = m \(\frac{{{v^2}}}{r}\)，可得 r = \(\frac{{mv}}{{qB}}\)。圆周运动的周期 T = \(\frac{{2\pi m}}{{qB}}\)。由此可见，电子在磁场中做匀速圆周运动的周期与速率 v 无关，因此两个电子同时回到出发点。

命题意图：了解带电粒子在匀强磁场中做匀速圆周运动的周期跟轨道半径 r 及速率 v 无关。

主要素养与水平：运动与相互作用观念（Ⅱ）；科学推理（Ⅱ）。

 

3．参考解答：（1）正确      （2）正确      （3）不正确，电子束圆周的半径会增大        （4）正确

命题意图：运用洛伦兹力分析带电粒子在匀强磁场中的圆周运动的半径大小。

主要素养与水平：运动与相互作用观念（Ⅱ）；科学推理（Ⅱ）。

 

4．参考解答：f = qvB

可得 v = \(\frac{f}{{qB}}\) = \(\frac{{3.2 \times {{10}^{ - 15}}}}{{1.6 \times {{10}^{ - 19}} \times 4 \times {{10}^{ - 3}}}}\) m/s = 5×10⁶ m/s

f = m \(\frac{{{v^2}}}{r}\)

可得 r = \(\frac{{m{v^2}}}{f}\) = \(\frac{{9.1 \times {{10}^{ - 31}} \times {{(5 \times {{10}^6})}^2}}}{{3.2 \times {{10}^{ - 15}}}}\) m = 7.11×10⁻³ m

T =  \(\frac{{2\pi r}}{v}\) =  \(\frac{{2 \times 3.14 \times 7.11 \times {{10}^{ - 3}}}}{{5 \times {{10}^6}}}\) s = 8.93×10⁻⁹ s

命题意图：运用洛伦兹力公式解答带电粒子在匀强磁场中的圆周运动问题。

主要素养与水平：科学推理（Ⅱ）；科学论证（Ⅱ）。

 

5．参考解答：离子经加速后射入速度选择器，以正离子为例，正离子在磁场中受到向左的洛伦兹力和向右的电场力作用。粒子源 P 和狭缝 S₃ 在一条直线上，意味着正离子水平方向不发生侧向偏转，所以能从速度选择器射出的离子应受力平衡，即满足受到的电场力和洛伦兹力大小相等，方向相反，则有

qE = qvB

可得：通过速度选择器后射入狭缝 S₃ 的离子速率需要满足的条件是 v = \(\frac{E}{B}\)。

命题意图：了解电场力和洛伦兹力都能使带电粒子偏转，理解质谱仪中速度选择器的原理和作用。

主要素养与水平：科学推理（Ⅲ）；科学本质（Ⅲ）。

 

6．参考解答：离子在 S₁ 和 S₂ 之间的电场中被加速，根据动能定理

qU = \(\frac{1}{2}\) mv² − 0

离子在匀强磁场中作匀速圆周运动，根据牛顿第二定律

qvB = m \(\frac{{{v^2}}}{r}\)

结合几何关系，轨道半径为

r = \(\frac{1}{2}\) d

由 ①、②、③ 式可证明离子的荷质比 (\frac{e}{m}\) = \(\frac{{8U}}{{{B^2}{d^2}}}\)

命题意图：理解质谱仪的基本原理，了解质谱仪如何测定带电粒子的荷质比。

主要素养与水平：运动与相互作用观念（Ⅳ）；能量观念（Ⅳ）；科学论证（Ⅳ）。

资料链接

带电粒子在匀强磁场中运动的一般情况

对于带电粒子的初速度 v 与匀强磁场的磁感应强度 B 成任一角度 ϕ 的情形，如图 10（a）所示，粒子的速度可分解成平行于 B 的分量 v_‖ = vcosϕ 及垂直于 B 的分量 v_⊥ = vsinϕ。如果只有垂直分量 v_⊥，粒子将受到洛伦兹力的作用在垂直于磁场的平面内做匀速圆周运动，圆周半径 r = \(\frac{{m{v_ \bot }}}{{qB}}\)；如果只有平行分量 v_‖，粒子将不受洛伦兹力，因而沿磁场方向做匀速直线运动。这两方面运动合成的结果是粒子做如图 10（b）所示的等螺距螺旋运动，螺旋的螺距（即粒子在绕行一周的时间 T 内沿磁场方向运动的路程）p = v_‖T = vcosϕ \(\frac{{2\pi m}}{{qB}}\)。

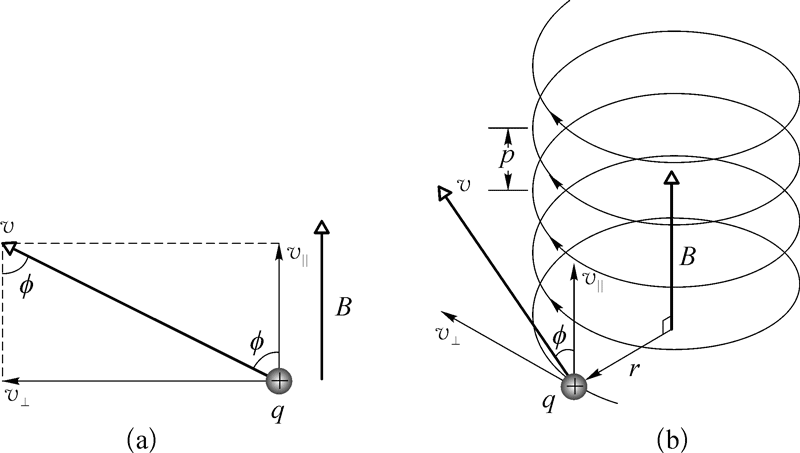
图 10

磁流体发电机

磁流体发电技术是一种新型的高效发电方式，由于无需经过机械转换环节，燃料利用效率显著提高。用燃料直接加热气体，使之在高温下电离成导电的离子流，然后让其在磁场中高速流动，在洛伦兹力作用下产生感应电动势，即由热能直接转换成电能。这种技术也称为等离子体发电。在几千摄氏度的高温下，这些物质中的原子和电子的运动都很剧烈，有些外层电子甚至可以脱离原子核的束缚，其结果使这些原子变成自由电子和失去电子的正离子，这就是等离子体。将等离子体以超音速的速度喷射到一个加有强磁场的管道里面，等离子体中带有正、负电荷的高速粒子在磁场中受到洛伦兹力的作用，分别向两极偏移，于是在两极之间产生电压，用导线接入电路中就可对外供电。磁流体发电本身的效率仅 20％ 左右，但由于其排烟温度很高，从磁流体发电机排出的气体可送往一般锅炉继续燃烧成蒸汽驱动汽轮机发电，组成高效的联合循环发电，总的热效率可达 50％ ~ 60％。

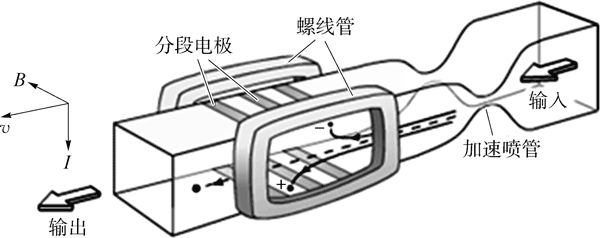
图 11

阴极射线荷质比的测定和电子的发现

带电粒子的电荷量与质量之比叫做荷质比。阴极射线是从高电压真空管的阴极发射出来的，是在研究低压气体放电时发现的。1894 年，英国物理学家 J．J．汤姆孙测出阴极射线的速度比光速小三个数量级，断定阴极射线是带负电的粒子流，否定了此前认为阴极射线是电磁波的看法。

1897 年，汤姆孙做了测量阴极射线粒子荷质比的实验，由此发现了电子。汤姆孙测量阴极射线粒子荷质比的实验装置原理图如图 12 所示。玻璃管内抽成真空，在阳极 A₁ 和阴极 K 之间维持数千伏的高电压，管内残存气体的离子撞击阴极引起的二次发射产生阴极射线。阳极 A₁ 是紧固在玻璃管中的接地金属环，A₂ 是另一接地金属环，A₁ 和 A₂ 中央的小孔使得在 K 和 A₁ 之间加速的粒子通过小孔后形成窄束，打在玻璃管另一端荧光屏 S 的中央 O 点，形成光斑。玻璃管中央是电容器的两极板，接通电源后在竖直方向产生匀强电场 E，管外电磁铁在图中虚线区域内产生垂直纸面向里的匀强磁场。适当调节电场 E 和磁场 B，使粒子束在电场和磁场的作用下不发生偏转，以 e、v 和 m 分别表示粒子的电荷量、速率和质量，则应有 eE = evB。由这时 E 和 B 的数值可以测出粒子流的速率 v = \(\frac{E}{B}\)。

然后将电场撤去，粒子束在磁场区内将沿圆弧运动，此圆弧半径应为 R = \(\frac{{mv}}{{eB}}\)。因而粒子的荷质比为 \(\frac{e}{m}\) = \(\frac{v}{{RB}}\) = \(\frac{E}{{R{B^2}}}\)。离开磁场区后，粒子束将由于惯性继续运动，射在荧光屏上的 P 点。半径 R 可以从荧光屏上光点移动的距离 OP 和仪器中的一些几何参量确定下来。由此，根据上式可以求出粒子的荷质比 \(\frac{e}{m}\)，其值比当时已知的氢离子的荷质比大千余倍。汤姆孙采用不同金属材料制成阴极，在射线管中充入不同的稀薄气体，测出的阴极射线粒子的荷质比都很接近，进而用“电子”来命名了这种带电微粒。1909 年至 1913 年，密立根的油滴实验排除了阴极射线粒子荷质比比氢离子的荷质比大千余倍来源于带大量电荷的可能性，最后消除了汤姆孙实验关于电子是否真正存在的种种疑虑。

参考资料：赵凯华、张维善，新概念高中物理读本，第二册，人民教育出版社，2018年 11 月，3.3 节。

医用回旋加速器的工作原理简介

医用回旋加速器是用来生产医用放射性核素的设备，主要有粒子源、磁场、交变电场、粒子束流引出、轰击靶等系统组成。带电粒子在磁场和交变电场作用下，反复在磁场中做圆周运动并被交变电场反复加速，直至达到所需的粒子能量，通过粒子束流引出系统引出而轰击靶系统中的靶材料，从而获得 PET / CT（正电子发射型计算机断层成像 / X 射线 CT 成像仪）成像所必需的正电子放射性核素。

PET / CT利用图像融合技术，综合了 PET 的功能、分子代谢影像与 X – CT 精细解剖影像的优势，结合正电子放射性核素标记的多种分子“探针”的应用，在以下几方面具有极重要的作用：恶性肿瘤早期诊断与肿瘤分期分级，临床疗效评估与随访监测，良、恶性病变鉴别，协助临床治疗方案决策和放疗生物靶区确定，探索肿瘤生物学特征等；在心脑血管疾病、神经变性疾病、癫痫等疾病的诊断、评估等方面也有独特价值，临床应用不断增加。标记各种分子“探针”所必需的正电子放射性核素如 18F（氟 – 18）、11C（碳 – 11）、13N（氮 – 13）等的半衰期一般都很短，因此依赖于医用回旋加速器的即时生产和制备。随着我国 PET / CT 应用的迅速发展，对医用回旋加速器的需求也快速增长。