第四章 第一节 光的折射
第四章
人类对光的研究可以追溯到公元前 1 000 多年。我国战国初期的思想家墨子的著作中记载了丰富的光学知识。古希腊数学家欧几里得的著作也描述了当时所了解的光学现象。直到 17 世纪前半叶,人们对于光的认识还仅限于光的直线传播及光的反射、折射现象。对光本质的认识经历了一个漫长的过程。光的波动说与微粒说之争始于 17 世纪初,其间经历了通过光的干涉和衍射实验证实光具有波动性,建立光的电磁波理论的过程。直至 20 世纪初,人们才认识到光具有波粒二象性。
在初中阶段,我们已经学习过光的反射和折射现象的相关知识。在本章中,将理解光的折射定律;知道光的全反射现象,了解光的干涉、衍射和偏振现象以及发生这些现象的条件;知道光是横波;了解激光的特性。在学习中,通过对光具有波动性的论证,增强证据意识,提升科学论证能力。通过实验发展科学探究能力;在观察实验现象的过程中,提升科学思维能力,形成科学态度。本章也是学习电磁波、波粒二象性等知识的基础。
站在清澈的湖边,你是否有过这样的体验,同时看到湖旁景物的倒影和水底的枯枝,如图 4–1 所示。这是来自景物和枯枝的光分别在水面发生反射和折射后,同时进入眼睛产生的视觉效果。

图 4–1 水中景象
图 4–2 光在两种介质表面的反射与折射
在初中我们已经学习了光的有关知识,如图 4–2 所示,光从介质 1 射到介质 1 与介质 2 的分界面时,一部分光会返回到介质 1,我们把这种现象称为光的反射。光的反射遵循光的反射定律。在发生反射现象的同时,还有一部分光进入了介质 2,并改变了传播的方向,这就是光的折射现象。
在光的折射现象中,改变入射光的方向,折射光的方向也随之改变。入射光线与法线的夹角为入射角,折射光线与法线的夹角为折射角。折射角随着入射角的变化而变化。
入射角和折射角之间有什么定量关系?下面我们通过实验研究光从空气斜射入水中时,入射角与折射角之间的定量关系。
图 4–3 光从圆盘盘心处射入水槽
如图 4–3 所示,画有方格的圆盘竖直插入水槽,水面恰好位于水平直径 PQ 处。在盘边缘固定激光笔,激光笔射出的光由空气沿半径 AO 斜射入水中,光发生折射,折射光线为 OB。由于圆盘半径一定,通过比较光线 AO、OB 在水面与法线方向的投影,即可得入射角 θ1、折射角 θ2 的各种信息。选择不同的入射角,在表 4–1 中记录数据,据此分析 θ1 与 θ2 之间的定量关系。
表 4-1
|
实验序号 |
OC |
OD |
AC |
BD |
|---|---|---|---|---|
|
1 |
|
|
|
|
|
2 |
|
|
|
|
|
3 |
|
|
|
|
|
4 |
|
|
|
|
从上面的实验可以看出,AC 与 BD 的比值为常数。如何将 AC 与 BD 的关系转化为 θ1 与 θ2 的关系呢?
设圆盘半径为 R,则有
\[\frac{{AC}}{{BD}} = \frac{{R\sin {\theta _1}}}{{R\sin {\theta _2}}} = \frac{{\sin {\theta _1}}}{{\sin {\theta _2}}}\]
斯涅耳(W. Snell,1580—1626)在分析了大量数据后,总结出光的折射定律(law of refraction):当光从介质 1 射入介质 2 时,折射光线与入射光线、法线处在同一平面内,折射光线与入射光线分别位于法线的两侧;入射角 θ1 的正弦与折射角 θ2 的正弦之比为一常数,即
\[\color{#62547B}\frac{{\sin {\theta _1}}}{{\sin {\theta _2}}} = C\]
在光的折射现象中,光路也是可逆的。图 4–3 所示的实验中,如果光沿 BO 从水下入射,折射后进入空气中的光将沿 OA 方向。
光在两种介质的分界面发生折射现象时,入射角的正弦与折射角的正弦之比为常数,该常数与入射角和折射角的大小均无关。但是,对于不同的介质,这个常数不同。
研究表明,常数 C 与光在介质中的速度有关,以 v1 表示光在介质 1 中的速度,v2 表示光在介质 2 中的速度,常数 C = \(\frac{{{v_1}}}{{{v_2}}}\)。
当光从真空斜射入某种介质时,把常数 C(即入射角 θ1 的正弦与折射角 θ2 的正弦的比值)称为这种介质的折射率(refractive index),用符号 n 表示。
\[\color{#62547B}n = \frac{{\sin {\theta _1}}}{{\sin {\theta _2}}}\]
光在真空中的速度为 c,在介质中的速度为 v,折射率也可表示为
\[\color{#62547B}n = \frac{c}{v}\]
由于光在真空中的速度大于其在介质中的速度,所以介质的折射率都大于 1。折射率决定了光从真空斜射入介质时的偏折程度,反映了介质的光学性质。
在实际中,通常遇到光从空气射入某种介质,或者从某种介质射入空气的情况。由于光在空气中的速度接近光在真空中的速度,空气的折射率近似为 1。可认为光由空气进入介质的折射情况与光由真空进入介质的折射情况相同。 此时同样可以用折射率 n 反映光从空气斜射入介质时的偏折程度。表 4–2 中列举了几种介质的折射率。
表 4–2 几种介质的折射率
|
介质 |
折射率 |
介质 |
折射率 |
|---|---|---|---|
|
合成碳硅石 |
2.65 |
水晶 |
1.54 |
|
金刚石 |
2.42 |
酒精 |
1.36 |
|
二硫化碳 |
1.63 |
水 |
1.33 |
|
玻璃 |
1.2~1.8 |
空气 |
1.000 28 |
对于两种不同介质,光在其中传播的速度大小不同,不同介质的折射率就不同。把折射率较小的介质称为光疏介质(optically thinner medium),折射率较大的介质称为光密介质(optically denser medium)。光疏介质与光密介质是相对而言的,例如,水、水晶和金刚石三种介质相比较,水晶相对于水是光密介质,而相对于金刚石则是光疏介质。
当光从折射率为 n1 的介质以入射角 θ1 入射到折射率为 n2 的介质时,折射角为 θ2。利用折射定律和折射率的定义推导:折射定律可以表示为 n1sinθ1 = n2sinθ2。并讨论光从光疏介质入射到光密介质或从光密介质入射到光疏介质时,光线偏折现象有什么不同。
无论光是由光疏介质入射到光密介质还是由光密介质入射到光疏介质,折射角都随入射角增大而增大。
生活中的很多现象都与光的折射有关。如图 4–4 所示,日落时,我们看到椭圆状的太阳逐渐沉入地平线。这是因为大气的密度随高度的减小而增大,离地面越近,大气的密度越大,光在其中的传播速度越小,折射率越大;来自太阳的光线在穿过大气层的过程中发生了折射,逐渐向地面弯曲;沿着地面观察者的视线看来,光线似乎是从较高的位置射过来的,太阳被“抬高”了。如图 4–5 所示,由于落日上缘和下缘发出的光在大气中的折射情况不同,落日看起来呈椭圆形。大气的折射同样会对星体位置的观察造成偏差,这是天文学家在地球上进行天文观测时必须考虑的因素。

图 4–4 日落时观察到椭圆状的太阳
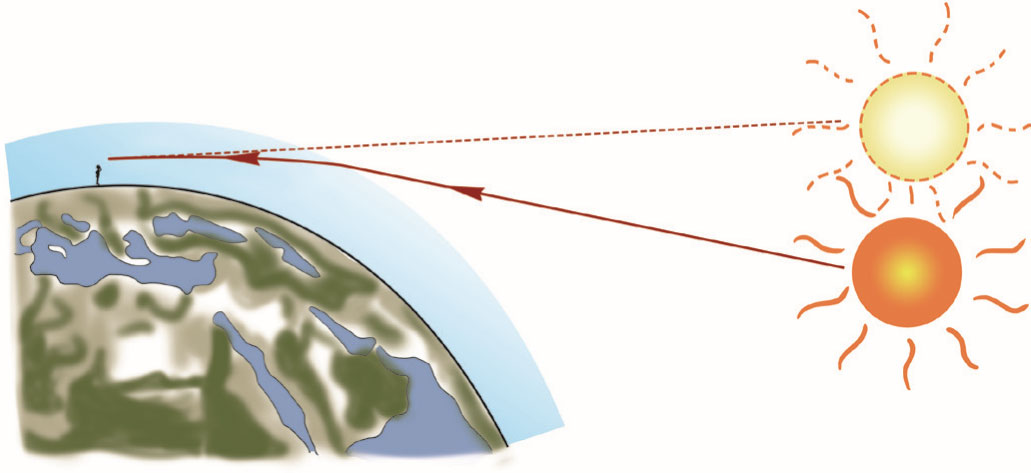
图 4–5 观察落日的示意图
折射率是物质的一种物理属性,常被用作检测食品的一项指标。例如,通过折射率的测定,可以控制高浓度葡萄糖浆的浓度,确定果汁饮料的含糖量,鉴别食用油中脂肪酸的构成,测定牛乳乳清的乳糖含量,快速区分甲醇与乙醇,等等,从而有效打击伪劣产品,维护市场秩序。
测量玻璃的折射率
提出问题
折射率是反映介质光学性质的一个重要参数。光从一种介质进入另一种介质时,折射光的传播路径与折射率有关。入射光从空气进入玻璃时,如何确定光在玻璃中的传播路径,并由此测量玻璃的折射率?
实验原理与方案
光在同一种均匀介质中沿直线传播,两点可确定一条光线。当光从空气斜射入另一种
介质时会发生偏折,其规律满足折射定律。
通过测绘射入和射出玻璃砖的光线,确定光在玻璃砖中的传播路径,可得光从空气入射到玻璃界面处的入射角 θ1 和折射角 θ2,根据折射定律计算得到玻璃的折射率。
图 4–6 测量玻璃的折射率
实验装置与方法
实验装置如图 4–6 所示。
用大头针分别确定入射光线和出射光线,通过作图找出光线在玻璃砖两个平行表面的入射点和出射点,两点的连线就是光在玻璃砖中的传播路径。
实验操作与数据收集
按照玻璃砖的宽度在白纸上画出两条平行直线,将玻璃砖依平行线置于白纸上。在玻璃砖的一侧垂直于纸面插两枚大头针 a、b,其连线与玻璃砖表面成一定角度。在另一侧透过玻璃砖观察,并在该侧的适当位置再插两枚大头针 c、d,使四枚大头针依次遮挡。此时,它们位于同一条射入眼睛的光线上,如图 4–6 所示。根据大头针的位置在白纸上画出入射光线和出射光线,确定入射点和出射点,画出玻璃砖中的折射光线。
测量并记录光在空气和玻璃分界面上的入射角 θ1 和折射角 θ2。改变入射角,再次测量,将数据记录在自己设计的表格中。
数据分析
根据测得的入射角和折射角,计算两者正弦的比值。
实验结论
玻璃的折射率 n =_________。
交流与讨论
交流各组的测量结果,讨论如果只有刻度尺,如何测量和处理数据。
如果准备插第三枚大头针时,发现透过玻璃砖观察不到前两枚大头针,原因是什么?
示例 人的双眼看到的图像信息经大脑处理后,产生了空间深度。站在游泳池边上观察池底时感觉深度(视觉深度)比池壁所标的数值 h 要小。通过计算解释这一现象。
分析:视觉深度小于实际深度的原因是从池底某点发出的光线经水面折射进入双眼产生的视觉效果。为此可以简化为由池底某点发出两条夹角较小的光线经水面折射进入空气。根据几何关系推算视觉深度。
图 4–7 分析光的折射
解:如图 4–7 所示,从池底的 A 点画两条光线 AB 和 AO,AB 沿竖直方向,AO 与竖直方向偏离一个角度 θ1。AO 经水面折射偏离了原来的方向,与竖直方向的偏角为 θ2。折射光线的反向延长线与 AB 相交于 C,BC 大小即为视觉深度。
由表 4–2 可知,水的折射率 n = 1.33。在直角三角形 OBA 中
\[OB = AB\tan {\theta _1}\]
根据光路可逆,可以反向看作光线从空气射入水中,根据折射定律
\[n = \frac{{\sin {\theta _2}}}{{\sin {\theta _1}}}\]
在直角三角形 OBC 中
BC = OBcot θ2 = ABtan θ1×cot θ2 = AB ×\(\frac{{\tan {\theta _1}}}{{\tan{\theta _2}}}\)
当角度 θ1 很小时,θ2 也很小
sin θ1 ≈ tan θ1,sin θ2 ≈ tan θ2
则 \(\frac{{BC}}{{AB}} = \frac{{\tan {\theta _1}}}{{\tan {\theta _2}}} = \frac{{\sin {\theta _1}}}{{\sin {\theta _2}}} = \frac{1}{n} \approx \frac{3}{4}\)
可见,池水的视觉深度约为实际深度的 \(\frac{3}{4}\)。
- 如图 4–8 所示为光从空气射入半圆形玻璃砖再从玻璃砖射入空气的光路图,O 为半圆形砖的圆心。指出哪些情况是可能发生的,哪些是不可能发生的,并说明理由。
图 4–8
图 4–9
- 如图 4–9 所示,一束光线斜射入容器中,并在容器底部形成一个光斑。往容器中逐渐注水的过程中,图中的光斑的位置将如何变化?
- 把一块厚玻璃板压在水平放置的纸上,透过玻璃板看纸上的字迹与直接看纸上的字迹会有什么不同?试解释发生这种现象的原因。
- 诗句“大漠孤烟直,长河落日圆”给我们展现了一幅美丽的画卷。当诗人看到落日接近地平线之时,太阳的实际位置已经位于地平线下方了。分析这种现象的原因是什么?
- 某同学通过实验研究光的折射。表 4–3 记录的是光从空气以不同角度射入水中的实验数据,表 4–4 记录的是光从空气射入某种透明介质的实验数据。
(1)由表 4–3 和表 4–4 的数据,判断这种透明介质和水的折射率哪个更大。简述判断依据。
(2)根据表 4–4 的数据,结合表 4–2“几种介质的折射率”,判断这种透明介质可能是哪种材料。
表 4–3
|
入射角 i |
0° |
30° |
45° |
60° |
|---|---|---|---|---|
|
折射角 r |
0° |
22° |
32° |
40° |
表 4–4
|
入射角 i |
0° |
30° |
45° |
60° |
|---|---|---|---|---|
|
折射角 r |
0° |
17° |
24° |
30° |
图 4–10
- 如图 4–10 所示,一束光从空气斜射入某介质,入射光线与反射光线的夹角为 90°,折射光线与入射光线延长线的夹角 θ 为 15°,该介质的折射率和光在该介质中传播的速度分别为多少?
本节编写思路
本节从生活情境引入,通过探究建立光的折射定律和折射率的概念,并用所得规律测量介质的折射率。本节内容按以下思路展开:
1.探究得出光的折射定律、建立折射率的概念。知道折射率反映了介质的光学性质、介质中的光速与折射率有关。
2.用插针法测量介质的折射率,进一步体验用光线形象描述光的传播的方法。
3.根据光的折射定律和折射率的概念,分析相关的实际现象或问题,了解折射率在生产技术中的应用。
学习本节内容,将经历实验探究、实验测量以及运用概念和规律分析实际现象或问题等过程。由此建立光的折射定律和折射率的概念、了解介质中光速与折射率的关系,发展实验观测技能和分析推理能力,提高探究物理问题的兴趣、增强团队合作的意识,体验实事求是、认真细致对实验探究和测量的重要性,感悟物理规律与生产技术和生活之间的关系。
正文解读
以照片中的自然风光为情境,观察水面上景物的倒影、水底树木的枝条,引导学生回顾光在介质表面的反射定律和折射现象,为定量探究光的折射定律做准备。
这是一个让学生动手实验探究的“自主活动”。目的在于引导学生在初中定性实验的基础上,进一步通过小组合作探究折射角与入射角的定量关系。本实验的设计思路是:改变入射角,用圆盘上的方格测得入射光和折射光在法线方向、平行界面方向的投影长度,分析和处理数据,得出入射角与折射角的正弦之比为常数的结论。
公元 140 年,托勒密曾认为在光的折射现象中,入射角 θ1 与折射角 θ2 之间存在简单的正比关系,并且通过实验测量得到光从空气斜射入水中时 θ2 = 0.7θ1 的结论。后来人们发现,上述结论只在入射角较小时才大致成立。实际上,由于小角度时 sinθ ≈ θ,托勒密的结论正是折射定律在入射角较小时的近似。
实验时应注意,使圆盘的中心 O 始终在分界面上并作为光的入射点。这样,在半径一定的情况下,入射角和折射角的三角函数,可以用图 4 – 3 中的线段长度表示,\(\frac{{{\rm{AC}}}}{{{\rm{BD}}}}\) 为入射角与折射角的正弦之比,\(\frac{{{\rm{OC}}}}{{{\rm{OD}}}}\) 为入射角与折射角的余弦之比。
此处可引导学生联系机械波的折射现象,感受光和机械波在传播规律上相似。另外,在定量探究得出光的折射定律后,可以借助实验进一步验证折射现象中光路的可逆性。
将表 4 – 2 中几种介质的折射率由大到小排序,发现并非介质的密度越大折射率就越大。如水的密度比酒精大,折射率却比酒精小。
这是一个让学生推理的“自主活动”。要求学生针对光从折射率为 n1 的介质斜射入折射率为 n2 的介质的一般情况,综合运用折射定律 \(\frac{{\sin {\theta _1}}}{{\sin {\theta _2}}}\) = C = \(\frac{{{v_1}}}{{{v_2}}}\),介质折射率的概念及其与光速的关系式 n1 = \(\frac{c}{{{v_1}}}\),n2 = \(\frac{c}{{{v_2}}}\),导出折射定律的表达式 n1sinθ1 = n2sinθ2。据此认识光在两种介质分界面发生折射时折射角与入射角相对大小的关系,为全反射的学习做准备。
从地面观察太阳东升西落的景象或星体的位置,看到的景象或位置与实际情况有偏差。原因在于,光从太阳或星体射向地面,在大气层中是从光疏介质向光密介质传播,大气的折射率连续变化,光由于折射而逐渐向地面弯曲。这与地面上看到的“海市蜃楼”在原理上是相同的。
此处设置“STSE”栏目,使学生了解折射率在食品成分检测中的作用,进一步认识折射率是物质本身的光学属性,知道物理规律是食品安全快速检测技术的基础。
这是一个课标规定的“学生实验”,需利用插针法画出光在玻璃砖中的折射光线,得到玻璃的折射率。有关实验的具体讨论或说明可见物理实验与活动部分。
本“示例”示范了解答几何光学问题的一般思路和步骤,如画出相应的光路图,做出必要的分析和运算。“视觉深度”与观察者的视线方向有关。题中取入射角、折射角的小角度进行近似计算,得到的仅是观察者以接近垂直水面方向看池底情况下的视觉深度。若观察方向逐渐偏离,越接近水面方向,视觉深度越小;视线接近平行于水面观察时视觉深度接近零。
问题与思考解读
1.参考解答:图(a)不可能会发生,理由是:光从玻璃砖斜射入空气时会发生光偏离原来传播方向的折射现象。图(b)可能会发生,理由是:光从玻璃砖斜射入空气,折射角大于入射角,符合光从光密介质斜射入光疏介质的折射规律。图(c)可能会发生,理由是:光从空气斜射入玻璃砖,折射角小于入射角,符合光从光疏介质斜射入光密介质的折射规律。图(d)不可能会发生,理由是:光从空气斜射入玻璃砖,折射角应小于入射角。
提示:不需要确定具体的角度数值。
命题意图:知道光垂直两种介质界面入射时方向不改变,光斜射入介质界面时,将发生折射现象;根据生活实际做出正确判断。
主要素养与水平:科学推理(Ⅱ)。
2.参考解答:由图 1 可知,往容器中注水的过程中,光斑慢慢向左移动提示:不要求讨论光斑的形状变化。

命题意图:关注因为光发生折射引起光斑位置变化的现象。
主要素养与水平:科学推理(Ⅱ);科学本质(Ⅰ)。
3.参考解答:当视线与玻璃板表面垂直时,透过玻璃板看到的字迹上浮,原因正如教材中示例解释所表明的那样,字迹的视觉深度比实际深度小。当视线与玻璃表面不垂直时,看到的字迹的位置不仅有上下的变化还存在水平方向的偏移,原因是来自字迹从玻璃砖上表面出射的光线反向延长形成的虚像的位置相对字迹的位置发生了水平偏移。
提示:不要求通过画严格的光路图进行解释。
命题意图:会用简洁的语言描述观察到的现象,并根据光从玻璃射向空气的折射现象,加以定性的解释。
主要素养与水平:物质观念(Ⅰ);科学推理(Ⅱ)。
4.参考解答:正如教材图 4 – 5 所示,越靠近地面,大气的折射率越大。太阳光在大气层内发生了连续的折射,逐渐弯曲。
命题意图:关注教材中的示意图,用示意图提供的信息,做出解释。
主要素养与水平:物质观念(Ⅰ)。
5.参考解答:(1)由折射率关系式 n = \(\frac{{\sin i}}{{\sin r}}\),通过比较表 4 – 3 和表 4 – 4 的数据可知,水的折射率 n1 = \(\frac{{\sin {i_1}}}{{\sin {r_1}}}\),透明介质的折射率 n2 = \(\frac{{\sin {i_2}}}{{\sin {r_2}}}\),由于入射角 i 相同,折射角 r1 > r2,即 sin r1 > sin r2,n1 < n2
(2)根据表 4 – 4 的数据可知,光从空气进入某种透明介质,折射率 n2 = \(\frac{{\sin i}}{{\sin r}}\) ≈ 1.73,查表 4 – 2 可得,这种透明介质可能是玻璃。
提示:也可根据表中的数据,计算出水和透明介质的折射率 n 的大小,直接比较 n 的大小。
命题意图:能在控制入射角大小的前提下,比较折射角,理解折射率的意义;从获得的证据做出合理的推断。
主要素养与水平:科学论证(Ⅲ);解释(Ⅲ)。
6.参考解答:(1)由反射定律可知入射角 α 等于反射角 β,由于 α + β = 90°,故 α = 45°;设折射角为 γ,则由图 4 – 10 可知,γ + θ = α = 45°,由于 θ =15°,故折射角 γ = 30°,所以该介质的折射率 n = \(\frac{{\sin \alpha }}{{\sin \gamma }}\) = \(\frac{{\sin 45^\circ }}{{\sin 30^\circ }}\) = \(\sqrt 2 \)
(2)由折射率与速度的关系 n = \(\frac{c}{v}\),得 v = \(\frac{c}{n}\) = \(\frac{{3 \times {{10}^8}}}{{\sqrt 2 }}\) m/s ≈ 2.12×108 m/s
命题意图:知道光发生反射、折射时入射角与反射角、折射角的关系,做出几何关系的推断,结合折射定律得出折射率咒;知道光在不同介质中的速度与折射率的关系。
主要素养与水平:解释(Ⅲ);科学论证(Ⅱ)。
资料链接
惠更斯原理与光的折射定律
荷兰物理学家克里斯蒂安·惠更斯(Christiaan Huygens)在创立光的波动说时首先提出:行进中的波阵面上任一点都可看作是新的次波源,而从波阵面上各点发出的许多次波所形成的包络面,就是原波面在一定时间内所传播到的新波面。这一内容被称为惠更斯原理。利用惠更斯原理,可以导出光的反射定律和折射定律。
如图 2 所示,设想一束平行光(平面波)以入射角 i1 由介质 1 射向它与介质 2 的分界面上,其边缘光线 1 到达 A1 点。作通过 A1 点的波面,它与所有入射光垂直。在光线 1 到达 A1 点的同时,光线 2,3,…,n 到达此波面上的 A2,A3,…,An 点。设光在介质 1 中的速度为 v1,则光线 2,3,…,n 分别要经过一段时间 t2 = \(\frac{{{A_2}{B_2}}}{{{v_1}}}\),\(\frac{{{A_3}{B_32}}}{{{v_1}}}\),…\(\frac{{{A_n}{B_n}}}{{{v_1}}}\),后才到达分界面上的 B2,B3,…,Bn 点。每条光线到达分界面上时都同时发射两个次波,一个是向介质 1 内发射的反射次波,另一个是向介质 2 内发射的透射次波。设光在介质 2 中的速度为 v2,在第 n 条光线到达 Bn 的同时,由 A1 点发出的反射次波波面和透射次波波面分别是半径为 v1tn 和 v2tn 的半球面。
<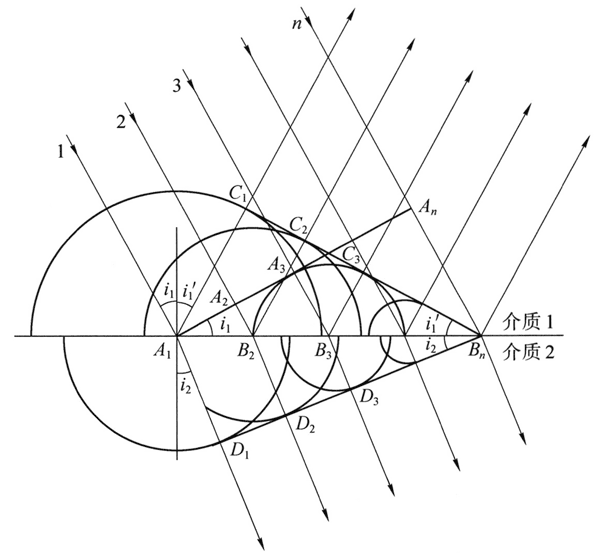
与此同时,光线 2,3,…,n 传播到 B2,B3,…,Bn 各点后发出的反射次波波面的半径分别为 v1(tn – t2),v1(tn – t3),…而透射次波面的半径为 v2(tn – t2),v2(tn – t3),…这些次波面一个比一个小,直到 Bn 处缩成一个点。根据惠更斯原理,此刻波面是这些次波面的包络面。不难证明,反射次波和透射次波的包络面都是通过 Bn 的平面。设反射波的波面与各次波面相切于 C1,C2,C3,…各点,而透射波的波面与各次波面相切于 D1,D2,D3,…连接次波源和切点,即得到波线;A1C1,B2C2,B3C3,…为反射光线,A1D1,B2D2,B3D3,…为折射光线。
由于 A1C1 = AnBn = v1tn,△A1C1Bn 和 △BnAnA1 全等,因而 ∠AnA1Bn = ∠C1BnA1,由图 2 中不难看出,入射角 i1 等于反射角 i1ʹ 这样就得到了反射定律。还可以看出,∠D1BnA1 = i2,可得:
sin i1 = \(\frac{{{A_n}{B_n}}}{{{A_1}{B_n}}}\) = \(\frac{{{v_1}{t_n}}}{{{A_1}{B_n}}}\),
sin i2 = \(\frac{{{A_1}{D_1}}}{{{A_1}{B_n}}}\) = \(\frac{{{v_2}{t_n}}}{{{A_1}{B_n}}}\),
故 \(\frac{{\sin {i_1}}}{{\sin {i_2}}}\) = \(\frac{{{v_1}}}{{{v_2}}}\)
即入射角与折射角的正弦之比为一常数。这样便导出了折射定律。
实际上,利用惠更斯原理同样可以解释机械波的传播、反射和折射等现象。
(选自赵凯华《新概念物理教程光学》,高等教育出版社 2004 年版,此处有增删)
发布时间:2022/6/9 下午11:21:23 阅读次数:12031
