“测量玻璃折射率”实验归类例析

广东省中山纪念中学 刘颢 选自《中学物理教学参考》2009年第4期

“测量玻璃的折射率”实验原理简单，操作简便。也正因为如此，以它为命题内容来考查学生时，如果不加变换则学生对它基本上无思维障碍。为了考查学生能力，就必须对现有实验进行变换创新，而创新方向的不同带来了对此内容考查方法的多样性。

一、变换实验器材

上述实验要求有一块平行透明的玻璃砖，这是一特殊器材，没有这类透明玻璃砖时能否用其他性质的玻璃替代？从这个思路出发，于是有了下面的考法。

例1：（2006，全国卷Ⅱ）一块玻璃砖有两个相互平行的表面，其中一个表面是镀银表面光线不能通过。现要测定此玻璃砖的折射率。给定的器材还有：白纸、铅笔、大头针4枚（P₁、P₂、P₃、P₄）、带有刻度的直角三角板、量角器。

实验时，先将玻璃砖放到白纸上，使上述两个相互平行的表面与纸面垂直。在纸上画出直线aa′和bb′，aa′表示镀银的不透明玻璃表面，bb′表示另一表面，如图1所示。然后，在白纸上竖直插上两枚大头针P₁、P₂（位置如图1）。用P₁、P₂的连线表示入射光线。

（1）为了测量折射率，应如何正确使用大头针P₃、P₄？试在题图中标出P₃、P₄的位置。

（2）移去玻璃砖与大头针，试在题图中通过作图方法标出光线从空气到玻璃中的入射角θ₁与折射角θ₂。简要写出作图步骤。

（3）写出用θ₁、θ₂表示的折射率公式n＝             。

解析：（1）在bb′一侧观察P₁、P₂（经bb′折射、aa′反射，再经bb′折射后）的像，在适当位置插上大头针P₃，让P₃挡住P₁、P₂像；再插上大头针P₄让它挡住P₁、P₂像和P₃。P₃、P₄的位置如图2所示。

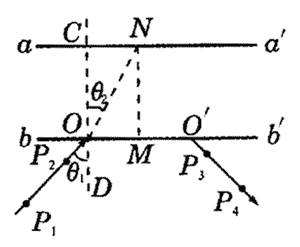（2）①过P₁、P₂作直线与交bb′于O；

②过P₃、P₄作直线与bb′交于O′；

③利用刻度尺找到OO′的中点M；

④过O点作bb′的垂线CD，过M点作bb′的垂线与aa′相交于N点，如图2所示，连接ON；

⑤量得∠P₁OD＝θ₁，∠CON=θ₂。

（3）n＝sinθ₁/sinθ₂

说明：教材用的是透明平行玻璃砖，而上述考法则把透明玻璃砖变换成反射式玻璃砖，其实验方法和原理是一样的，但考查的灵活性增强了，考查了学生对实验方法和原理的理解能力和应用能力。

二、变换实验方法

如例1所述，原实验利用插针法来确定光路，那么不用插针法行吗？从这个思路出发有了下面的考法。

例2：用半圆形玻璃砖测定玻璃折射率的方法如下：

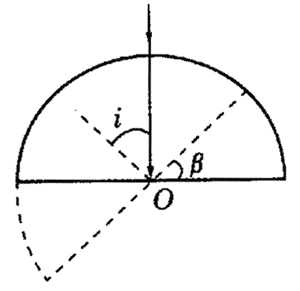（1）把半圆形玻璃砖放在白纸上，定出其圆心O，在白纸上用铅笔描下其直径和圆心位置，让一束光沿与直径垂直的方向穿入玻璃砖的圆弧部分，射到圆心O，如图3所示。

（2）不改变入射光的方向和位置，让玻璃砖以O点为轴逆时针转动到从玻璃砖平面一侧恰好看不到出射光为止。

（3）用铅笔描下此时玻璃砖直径的位置，移去玻璃砖测出玻璃砖转过的角度β，由β计算出折射率。若已知β＝42°，又查出sin42°＝0.67，则玻璃的折射率n＝           。

解析：这是利用光的全反射现象测定玻璃折射率的方法。光垂直射向玻璃砖的圆弧部分时光路沿直线传播，射到玻璃砖的平面部分后再折射出来，当入射角i增大到等于某值时刚好没有光线射出，此时的入射角i即玻璃的临界角，也就是玻璃砖平面转过的角度β。由全反射规律有n＝1/sinβ ＝1/sin42° ＝1.5。

说明：上述考法打破了用插针方法来确定光路的思维，而是利用全反射原理来确定折射光路；这里，通过变换实验方法考查了学生综合应用知识的能力。

三、变换实验数据处理方法

原实验用已知入射角i作为基准，通过插针方法来确定折射角r，然后用量角器量出角r，再用三角函数表查出其折射角所对应的正弦值，代入公式n＝sini/sinr 得出实验结果。这种处理很繁琐，那么还有其他的数据处理方法吗？从这种思路出发，于是有了下面的考法。

例3：某学生在做“测量玻璃的折射率”实验时，作完光路图后以O点为圆心、10.00cm长为半径画圆，分别交线段OA、OO′连线的延长线于A、C点，过A点作法线NN′的垂线AB交NN′于点B，过C点作法线NN′的垂线CD交NN′于D点，如图4所示。没有量角器无法测角度，这位学生于是用刻度尺量得AB＝6.00cm，CD=4.00cm，则该玻璃的折射率为           。

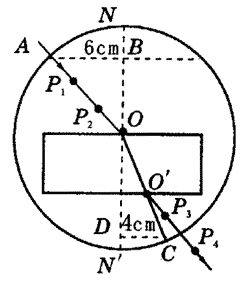
解析：由题意可知入射角i＝∠AOB，折射角r＝∠COD，则由折射率公式n＝sini/sinr ＝(AB/AO)/(CD/CO) ＝AB/CD 可解得n＝1.5。

说明：上述实验数据处理方法是用直角三角形的边与边对应关系替代三角函数，避免了没有数学用表和量角器时无法计算的尴尬；该考法可以考查学生灵活处理实验数据的能力。

四、变换误差分析方向

原实验的误差主要来源于实验时玻璃砖所放位置与所作光路图两平行界面的不重合。那么，如果变换实验仪器、实验方法或使光路图中两界面不平行，则实验误差分析方法又会怎样呢？于是有了以下几种考法。

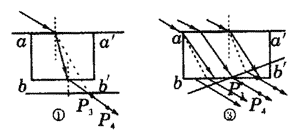
例4：用“插针法”测定透明半圆柱玻璃砖的折射率，O为玻璃截面的圆心，使入射光线跟玻璃砖平面垂直，如图5所示四个图中P₁、P₂、P₃、P₄是四个学生实验插针的结果。

（1）在图5所示四个图中肯定把针插错了位置的是           。

（2）在这四个图中可以比较准确地测定折射率的是             。

解析：分别连接P₁、P₂和P₃、P₄用以确定入射光线和出射光线的入射点与折射点，并连接该两点，可确定出射光线和玻璃砖内部折射光线，如图6所示。

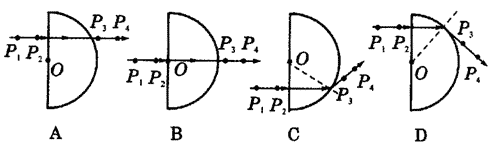
由图6可知，（1）图A把针插错了。（2）图B是r＝i＝0的特殊情况，不能测定n；图D入射角太大接近临界角，使出射光线弱、观察误差大；而图C的入射角适中，所以C比较准确。

例5：在用“插针法”测定玻璃砖折射率的实验中，甲、乙、丙三位同学在纸上画出的界面aa′、bb′与玻璃砖位置的关系分别如图7中的①、②和③所示，其中甲、丙用的是矩形玻璃砖，乙用的是梯形玻璃砖。他们的其他操作均正确，且均以aa′、bb′为界面画光路图，则甲、乙、丙三位同学测得的折射率与真实值相比分别为       、         、         （填“偏大”、“偏小”或“不变”）。

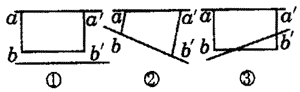
解析：由于乙画的aa′、bb′界面与玻璃砖两光学表面重合，所以测量值与真实值相等。如图8为①③两图中分别作出的实际光路图（图中实线）和以aa′、bb′为界面、以大头针所留痕迹作为出射光线画出的实验光路图（如图8中虚线所示）。

比较实际光路图与实验光路图的折射角关系可知：甲画的折射角测量值偏大，则折射率偏小；同理据③图可知，实际光路可能比实验光路的折射角小、也可能大、也可能相等，则丙画的折射率可能偏大、可能偏小、也可能不变。

说明：例4从实验原理、实验的可视性方向上考查实验误差分析，而例5则综合考查了几种误差现象，大大提高了对学生的能力要求。误差分析方向的变换，对学生误差分析能力提出了更高的要求。

五、实验的开放性拓展

例6：某研究小组的同学根据所学光学知识，设计了一个测液体折射率的仪器。如图9所示，在一圆盘上过其圆心O作两条互相垂直的直径BC、EF，在半径OA上垂直盘面插下两枚大头针P₁、P₂，并保持P₁、P₂位置不变；每次测量时让圆盘的BFC部分竖直浸入液体中，而且总使得液面与直径BC相平，EF作为界面的法线，而后在图中右上方区域观察P₁、P₂的像，并在圆周上插上大头针P₃，使P₃正好挡住P₁、P₂的像。同学们通过计算，预先在圆周EC部分刻好了折射率的值，这样只要根据P₃所插位置，就可直接读出液体折射率的值。

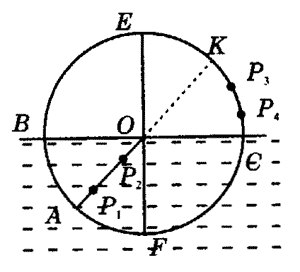
（1）若∠AOF＝30°，OP₃与OC的夹角为30°，则P₃处所对应的折射率值为 。

（2）图中P₃、P₄两位置哪一处所对应的折射率值大？答：             。

（3）作AO的延长线交圆周于K，K处所对应的折射率值应为             。

解析：这个装置可以说是一个简易的液体折射率测量装置。它的原理还是利用折射定律，只是入射角固定，而折射角的位置被刻好的折射率值所取代，从而可直接读取折射率。

（1）由折射定律有 n＝sin∠EOP₃/sin∠AOF ＝sin60°/sin30° ＝1.73。

（2）因入射角固定，折射角越大则折射率越大，而折射角∠EOP₃＜∠EOP₄，故P₄对应的折射率大。

（3）如果光线经过液体中的P₁、P₂后没有偏折，直射到K点，则该液体折射率为n＝1。

说明：上述实验的原理与操作方法与“测量玻璃折射率”一样，只不过这里变成了测量液体的折射率，而且可以测量各种透明液体的折射率；更重要的一点在于，它是可直接读出折射率的一种简易测量装置。所以这种变换不仅是实验题目的开放性拓展，更是实验方式的变革，甚至可以说它能变成一种产品。

对“测量玻璃折射率”实验的考查经过多年演变，通过变换实验器材、变换实验方法、变换实验数据处理方法、变换误差分析方向、实验的开放性拓展等，使考法多种多样，也从各个角度考查了学生理解和处理问题的能力。

从这里也可以看到，对教材上的一个简单实验，只要我们敢于创新从不同角度去理解、演绎它，就可挖掘出丰富多彩的内容。而高考所谓的创新试题不正是这样得出来的吗？与其考前猜题，还不如学习过程中有意识地按上述思路来对所学的各个知识点演绎变换一番。

发布时间：2010/1/26 上午7:30:06  阅读次数：20860