第九章 第五节 带电粒子在电场中的运动

图 9–35 北京正负电子对撞机的双储存环
带电粒子由于携带电荷,在电场中会受到电场力的作用产生加速度,使其速度发生变化。在现代科学实验和技术设备中,常常根据这个原理利用电场来改变或控制带电粒子的运动。北京正负电子对撞机是我国第一台高能加速器,也是世界八大高能加速器之一,如图 9–35 所示是该装置中的双储存环。该对撞机是高能物理研究的重大科技基础设施,它为中国粒子物理和同步辐射应用提供了基本研究实验手段和条件,使中国高能物理研究进入了世界前沿。而且,正负电子对撞机产生的同步辐射作为特殊光源,可在生物、医学、化学、材料等领域开展广泛的应用研究工作。
测量高度的起点不同,同一点的高度的数值就不相同,但两点间的高度差却保持不变。同样的道理,选择不同的位置作为电势零点,电场中任意点的电势的大小会随之改变,但电场中任意两点间的电势之差却保持不变。
电场中两点间电势之差称为电势差(electric potential difference),也叫电压。设电场中 A 点的电势为 φA,B 点的电势为 φA,A、B 两点间的电势差用符号 UAB 表示,则
\[\color{#975F85}{U_{AB}} = {\varphi _A} - {\varphi _B}\]
电势差是标量,只有大小,没有方向。当 A 点电势比 B 点电势高时,UAB 为正值;UBA 则为负值。在国际单位制中电势差的单位也是伏特,简称伏,用符号 V 表示。
把正电荷 q 沿电场线的方向从 A 点移到 B 点,若 A 点的电势为 φA,B 点的电势为 φB,电场力做正功 WAB,则有
\[\begin{array}{l}{W_{AB}} = {E_{\rm{p}}}_A - {E_{\rm{p}}}_B\\ = q{\varphi _A} - q{\varphi _B}\\ = q({\varphi _A} - {\varphi _B})\\ = q{U_{AB}}\end{array}\]
即 \(\color{#975F85} {U_{AB}} = \frac{{{W_{AB}}}}{q}\)
这就是电势差与电场力做功的关系,说明电场中任意两点之间的电势差数值上等于移动单位正电荷电场所做的功。因此,知道了电场中两点的电势差就可以方便地计算在这两点间移动电荷时电场力所做的功,而不必考虑电荷移动的路径。
示例 1 电场中有 A、B 两点,已知电势 φA = 650 V,φB = 800 V。把电荷量 q = −2×10−9 C 的带电粒子从 A 点移动到 B 点,则:
(1)A、B 两点间的电势差是多少?
(2)电场力做了多少功?做的是正功还是负功?
分析:根据 A、B 两点的电势可求出两点间电势之差。利用电场中某一点的电势与电荷量的乘积可求得带电粒子在该点所具有的电势能,根据电场力做功与电势能变化量的关系便可求解。
解:(1)A、B 两点间的电势差
\[\begin{array}{l}{U_{AB}} = {\varphi _A} - {\varphi _B}\\ \;\;\;\;\;\;= 650\;{\rm{V}} - 850\;{\rm{V}}\\ \;\;\;\;\;\;= - 150\;{\rm{V}}\end{array}\]
(2)带负电粒子在 A 点的电势能
\[\begin{array}{l}{E_{\rm{p}}}_A = q{\varphi _A}\\ \;\;\;\;\;\;= - 2 \times {10^{ - 9}} \times 650\;{\rm{J}}\\ \;\;\;\;\;\;= - 1.3 \times {10^{ - 6}}\;{\rm{J}}\end{array}\]
带负电粒子在 B 点的电势能
\[\begin{array}{l}{E_{\rm{p}}}_B = q{\varphi _B}\\ \;\;\;\;\;\;= - 2 \times {10^{ - 9}} \times 800\;{\rm{J}}\\ \;\;\;\;\;\;= - 1.6 \times {10^{ - 6}}\;{\rm{J}}\end{array}\]
带电粒子从 A 点移动到 B 点电场力所做的功
\[\begin{array}{l}{W_{AB}} = {E_{\rm{p}}}_A - {E_{\rm{p}}}_B\\ \;\;\;\;\;\;\;= - 1.3 \times {10^{ - 6}}\;{\rm{J}} - (1.6 \times {10^{ - 6}})\;{\rm{J}}\\ \;\;\;\;\;\;\;= 3 \times {10^{ - 7}}\;{\rm{J}}\end{array}\]
当然,也可以用公式 WAB = qUAB 进行计算,即
\[\begin{array}{l}{W_{AB}} = q{U_{AB}}\\ \;\;\;\;\;\;\;= ( - 2 \times {10^{ - 9}}{\rm{)}} \times ( - 150){\rm{J}}\\ \;\;\;\;\;\;\;= 3 \times {10^{ - 7}}{\rm{J}}\end{array}\]
因此电场力做功 3×10−7 J,做的是正功。
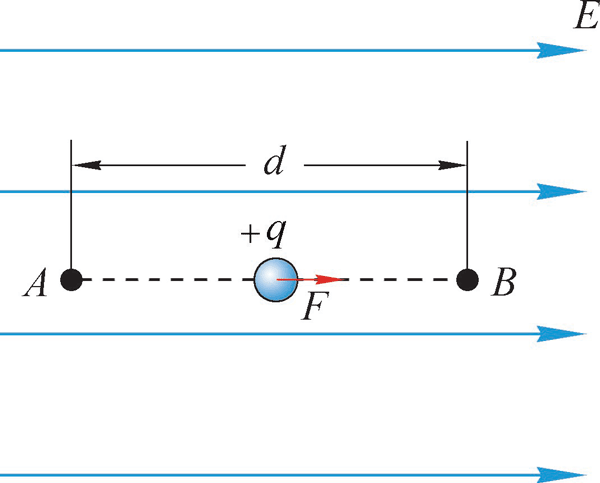
图 9–36 匀强电场中移动电荷
如图 9–36 所示,匀强电场的电场强度为 E,AB 间距离为 d、电势差为 UAB。把正电荷 q 沿电场方向从 A 点移动到 B 点,在此过程中,它所受的电场力为 qE,电场力对其做功 WAB = qEd。由电场力做功与电势差的关系,也可得 WAB = qUAB。
由此可得电场强度与电势差的关系为
\[\color{#975F85} E = \frac{{{U_{AB}}}}{d}\]
上式说明匀强电场中电场强度数值上等于沿电场线方向单位距离上降低的电势。而且,沿电场线的方向电势降低得最快。
请证明 1 N/C = 1 V/m。
(a)
(b)
图 9–37 a、b、c 三点在匀强电场中的关系
示例 2 如图 9–37(a)所示,在电场强度大小为 60 V/m 的匀强电场中有 a、b、c 三点,ab = 5 cm,bc = 8 cm,其中 ab 沿电场方向,bc 与电场方向的夹角为 60°。求:a、c 两点间的电势差 Uac。
分析:根据匀强电场中电场强度与电势差的关系 E = \(\frac{{{U_{ac}}}}{d}\),可得 Uac = Ed,其中 d 为 a、c 两点间沿电场线方向的距离或 a、c 两点所在等势面间的间距,如图 9–37(b)所示。
解:a、c 两点间沿电场线方向的距离
d = ab + bc·cos60° = ( 5 + 8×0.5 ) cm = 9 cm = 0.09 m
根据匀强电场中电场强度与电势差的关系,a、c 两点电势差的大小
\[\left| {{U_{ac}}} \right| = Ed = 60 \times 0.09\;{\rm{V}} = 5.4\;{\rm{V}}\]
因为沿电场线方向电势逐渐降低,φa > φb > φc,所以电势差 Uac 为正值。Uac = 5.4 V。
图 9–38 带电粒子
在电场中的加速
带电粒子在电场中受到电场力的作用,通常电场力远大于带电粒子的重力,从而可以忽略重力对带电粒子的影响。如图 9–38 所示,真空中有一对平行金属板,两板间电势差为 U,板间距为 d,将一质量为 m、带电荷量为 +q 的粒子在正极板附近由静止释放,分析带电粒子在电场中的运动情况。
带电粒子在匀强电场中做初速度为零的匀加速直线运动。为了求带电粒子到达负极板时速度 v 的大小,我们用两种方法来研究。
方法一:由于带电粒子在匀强电场中受到电场力 F 作用,从正极板出发做初速度为零匀加速直线运动,则由牛顿第二定律可得,带电粒子做匀加速直线运动的加速度
\[a = \frac{F}{m}\]
又 F = qE,由匀强电场的电场强度与电势差的关系 \(E = \frac{U}{d}\)
得到 \(a = \frac{{qU}}{{md}}\)
根据初速度为零的匀加速直线运动的运动学规律,则有
\[{v^2} = 2ad\]
可得 \(v = \sqrt {\frac{{2qU}}{m}} \)
方法二:带电粒子从正极板出发到达负极板,仅有电场力做功 W = qU,改变了带电粒子的动能,则根据动能定理,有
\[qU = \frac{1}{2}m{v^2} - \frac{1}{2}mv_0^2\]
由于 v0 = 0,也可得
\[v = \sqrt {\frac{{2qU}}{m}} \]
如果不是匀强电场,方法一和方法二中是否有些等式不适用了?请说明理由。
电荷在电场中运动会受到电场力的影响,必然获得加速度。因此,可以利用电场来控制带电粒子的运动。
阴极射线是从低压气体放电管的阴极射出的带负电的电子流。如图 9–39 所示即为用阴极射线管演示带电粒子在电场中的偏转的实验装置。
图 9–39 阴极射线在电场中偏转实验装置图
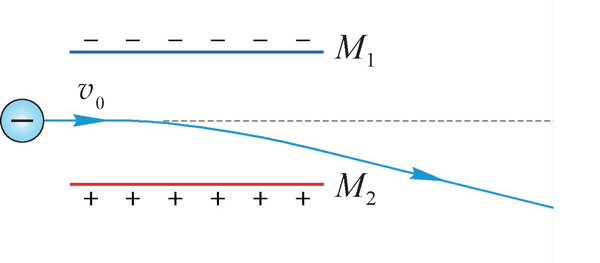
图 9–40 电子束在电场中的偏转
给阴极射线管左右两端加上高电压,电子束从阴极射向阳极。利用荧光屏可清晰地显示出电子束运动的径迹。在荧光屏前有一狭缝,射线只能从狭缝中通过沿直线前进。在射线经过路径的上下方有一对平行金属板 M1M2,称为偏转极板。通过控制偏转极板施加的电压观察带电粒子在电场中的偏转情况。
当平行金属板 M1M2 之间未加电压时,电子束不发生偏转,沿直线运动;当平行金属板 M1M2 之间施加上负下正的电压时,电子束在电场力的作用下如图 9–40 所示向下偏转;当平行金属板 M1M2 之间施加上正下负的电压,电子束将在电场力的作用下向上偏转。
带电粒子在电场中由于受到电场力的作用产生加速度,其速度大小和方向都可能发生变化。带电粒子在电场中沿直线加速和偏转是两种最基本的运动情况。
如图 9–41 所示,一电子(电荷量大小为 e、质量为 m)以初速度 v0 沿水平方向射入水平放置、相距 d、长为 L、电势差为 U(能使电子飞出极板)的一对平行金属板间。
设两极板间为向上的匀强电场。电子进入匀强电场后,由于重力通常远小于电场力,重力可忽略不计。忽略极板的边缘效应,电子受到竖直向下的电场力作用而发生偏转。电子的运动类似于重力场中的平抛运动。
电子在水平方向的分运动是速度为 v0 的匀速直线运动,即 vx = v0,因此电子在电场内运动的时间 t = \(\frac{L}{{{v_0}}}\)。
电子在竖直方向受电场力 eE 的作用,做初速为零、加速度为 a 的匀加速直线运动,产生垂直于板面方向偏移的距离 y = \(\frac{1}{2}\)at2。其中
\[a = \frac{F}{m} = \frac{{eE}}{m} = \frac{{eU}}{{md}}\]
所以 \(y = \frac{1}{2}a{t^2} = \frac{{eU{L^2}}}{{2mdv_0^2}}\)
电子离开电场时,速度 v 的竖直方向分量
\[{v_y} = at = \frac{{eU}}{{md}} \cdot \frac{L}{{{v_0}}}\]
偏转角度 θ 可由 tan θ 来确定,即
\[\tan \theta = \frac{{{v_y}}}{{{v_x}}} = \frac{{eU}}{{md}} \cdot \frac{L}{{v_0^2}}\]
- 在某次雷暴中,地面和云层之间的电势差是 1.2×109 V。假设一个电子从云层运动到地面,其电势能改变了多少?
- 电场中有 A、B 两点,已知两点的电势为 φA = 300 V,φB = − 200 V。将一电荷量为 + 4×10−6 C的粒子从 A 点移到 B 点,电场力对带电粒子做了多少功?做的是正功还是负功?带电粒子的电势能是增加还是减少?改变了多少?
- 如图 9–42 所示是一匀强电场的等势面,相邻等势面相距 2 cm,则该匀强电场的电场强度为多大,方向如何?
图 9–42
图 9–43
- 如图 9–43 所示,一束粒子从 O 点沿水平方向射入平行板之间的电场后分成了 a、b、c、d 四束,各粒子束中粒子的带电情况如何?(不计粒子重力)
- 如图 9–44 所示的装置处在真空中,电场加速电压为 U = 10 V,两极板间距离 d = 2 cm。若电子在负极板处由静止释放,求其在装置中被加速后离开电场时的速度 v。(电子的质量为 9.1×10−31 kg)
图 9–44
本节编写思路
本节通过与高度及高度差的类比,得出电场中任意两点间电势之差保持不变的结论,引出电势差的概念。
通过分析电场力做功与电势差的定量关系,可得电场中任意两点之间的电势差在数值上等于移动单位正电荷电场力所做的功。
通过分析、演绎得到匀强电场中电场强度和电势差的定量关系。
通过科学推理和科学论证,学会计算带电粒子在电场中沿直线运动的问题。通过自主活动实验研究带电粒子在电场中的偏转问题。
通过分析电场线和等势面之间的关系、电势差与电场强度的关系,体会科学研究应从不同角度展开。
体验分析和演绎的重要作用,感悟科学推理在科学研究中的重要性,构建运动与相互作用观念,培养科学推理和论证的能力。
正文解读
北京正负电子对撞机(BEPC)于 1988 年 10 月在中国科学院高能物理所建成。它由注入器、输运线、储存环、北京谱仪和同步辐射装置等几部分组成。对撞机的注入器是一台 200 m 长的直线加速器,用于为节首图所示的储存环提供能量为 1.1 ~ 1.55 GeV 的正负电子束。输运线连接注入器和储存环,将注入器输出的正负电子分别传送到储存环里。节首图所示的储存环是一台周长为 240.4 m 的环形加速器,它将正负电子如速到需要的能量,并加以储存。
本节可通过情境提出如何使带电粒子加速和偏转两大任务,然后逐项解决。帮助学生认识电场对带电粒子的作用,会计算带电粒子在电场中沿直线加速运动的问题,并通过实验了解带电粒子在电场中的偏转。
本节对带电粒子在电场中沿直线加速进行分析。“问题与思考”第 5 题的内容与此呼应。
理解电势差的概念,知道电势差与零电势的选择无关,具有绝对性。
引入电势差的概念亦可为下一章学习串联电路总电压等于各部分电压之和等电路知识做好铺垫,以便学生用电势差的概念分析电路。
通过示例 1 有关电场力做功的练习,可使学生体会电场力做的功既可由第四节电场力做功与电势能的变化之间的关系来计算,也可由本节电场力做功和电势差的定量关系来计算。
运用公式 WAB = qUAB 时,可将电荷量 q 和电势差 UAB 的正、负都代入计算,直接得到电场力做功的大小和正、负。也可将电荷量 q 和电势差 UAB 分别用绝对值代入计算,得出做功的大小后,再利用电荷所受电场力方向和移动方向判断电场力做功的正、负。体会从不同角度开展科学推理的过程。
对于电场中任意两点 A、B 间的电势差,表达式 UAB = Ed 仍然适用,但式中的 d 应理解为单位正电荷的位移矢量在电场方向上的投影。由功能关系可导出该式。若点电荷 q 在匀强电场中沿任意直线路径从 A 点移动到 B 点,设位移为 s,则从电场的能量属性可得电势能增量 ΔEAB = qUAB,从电场力做功的角度考虑有 WAB = Fscosθ = qEscosθ,由功能关系可得:UAB = Escosθ(scosθ = d,θ 为电场强度 E 与位移 s 方向的夹角),即匀强电场中两点间的电势差等于电场强度 E 的大小、位移 s 的大小、电场强度与位移夹角 θ 的余弦三者的乘积,这样就能得到电势差 UAB 的正、负,判断 A、B 两点电势的高低。
此处设置“大家谈”,是为了比较电场强度两种单位间的联系。电场强度的单位应是牛(顿)每库(仑)。在国际单位制中,符号为 N/C,数值上等于单位正电荷所受的电场力。电场强度的另一单位是伏(特)每米,符号是 V/m,它与 N/C 相等。常用的单位还有伏特每厘米,符号为 V/cm。
证明: 1 \(\frac{{\text{N}}}{{\text{C}}}\) = 1 \(\frac{{{\text{N}} \cdot {\text{m}}}}{{{\text{C}} \cdot {\text{m}}}}\) = 1 \(\frac{{\text{J}}}{{\text{C}}}\) · \(\frac{1}{{\text{m}}}\)。根据 UAB = \(\frac{{{W_{AB}}}}{q}\) 可知,电场中任意两点之间的电势差数值上等于移动单位电荷时电场力所做的功,1 V = 1 \(\frac{{\text{J}}}{{\text{C}}}\)。综上所述 1 N/C = 1 V/m。
通过初速度为零的带正电粒子在匀强电场中沿直线加速这种最简单的情况,解决节首图所提出的如何使带电粒子加速的任务。进一步通过“大家谈”引导解决非匀强电场的问题,学会计算带电粒子在电场中沿直线加速运动的不同情况。
此处设置“大家谈”,是为了讨论带电粒子在电场中沿直线加速问题时,运用动力学方法和运用动能定理求速度的区别与联系。
带电粒子在两平行金属板间匀强电场中加速的情境中,两种方法都适用。
如果不是匀强电场,方法二中的所有等式均适用,但方法一中的等式 E = \(\frac{U}{d}\) 不适用(详见本节资料链接)。因为这一等式仅适用于匀强电场,对于非匀强电场并不适用,也就不能得到 a = \(\frac{{qU}}{{md}}\)。
在电场中受电场力作用获得加速度,从而改变带电粒子的运动状态。不仅可以改变速度的大小,还能改变速度的方向。
本节中理论分析、演绎和计算的内容较多。本自主活动可采用电子束演示器(执行标准JY0017)的成套仪器供教师演示或学生自主活动。
这是一个观察型活动。其目的是:(1)观察电子束在电场中的偏转情况;(2)改变偏转极板电压的极性,观察电子束在电场中偏转情况的变化。
阴极射线是从低压气体放电管的阴极射出的带负电的电子流。在阴极射线管左、右两端连接直流高电压,阳极端接高电位,就会有电子束从阴极射向阳极。利用荧光屏可清晰地显示出电子束运动的径迹(电子束肉眼并不可见,但高速电子柬打到荧光屏表面时可使荧光粉发光)。在荧光屏前有一狭缝,射线(电子束)只能从狭缝中通过沿直线前进。在电子束经过路径的上、下方有一对平行金属板,称为偏转极板。通过控制偏转极板施加电压的正、负,观察电子束的偏转情况。通过改变偏转极板之间电压的大小,还可以人为控制电子束的偏转程度。
课程标准要求通过实验了解带电粒子在电场中的偏转。此处设置“拓展视野”,是为了探究“自主活动”中所显示的偏转现象,应用运动的合成和分解的思想进行分析。学生通过必修二的学习已有平抛运动的基础,类比平抛运动的规律学习带电粒子在电场中偏转的规律,理解人为控制电子束偏转程度的理论根据。
问题与思考解读
1.参考解答:ΔEp = | WAB | = qUAB = 1 × 1.2 × 109 eV = 1.2 × 109 eV,电势能减少 1.2 × 109 eV。
命题意图:带电云层下部大部分带负电荷,所以大多数的雷击是负极性的,雷云中的负电荷会在地面感应出大量正电荷。这样地面与带电云层之间,会形成强大的电场,雷击就是由电场对电子做功形成电流所致。
主要素养与水平:能量观念(Ⅱ);科学本质(Ⅰ)。
2.参考解答:A、B 两点间的电势差 UAB = (φA – φB = 300 V −(− 200)V = 500 V。由于 q = + 4 × 10−6 C,WAB = qUAB = 4 × 10−6 × 500 J = 2 × 10−3 J,电场力做正功,ΔEp = − WAB = − 2 × 10−3 J,电势能减少了 2 × 10−3 J。
命题意图:运用电场力做功与电势能变化的关系。
主要素养与水平:能量观念(Ⅱ);科学推理(Ⅱ)。
3.参考解答:电场强度大小:E = \(\frac{{{U_{AB}}}}{d}\) = \(\frac{2}{{0.02}}\) V/m = 100 V/m。电场强度的方向:垂直于等势面由电势高的等势面指向电势低的等势面(水平向左)。
命题意图:认识电场对带电粒子的作用,能分析带电粒子在电场中的运动情况。
主要素养与水平:运动与相互作用观念(Ⅱ)。
4.参考解答:两平行金属板间匀强电场方向竖直向下,带电粒子所受电场力方向与速度方向不在一直线上,故带电粒子在电场中做曲线运动。粒子束 a 向正极板偏转说明粒子束 a 带负电;粒子束 b 不发生偏转说明粒子束 b 不带电;粒子束 c、d 向负极板偏转说明粒子束 c 和 d 带正电。
命题意图:分析匀强电场中电场线和等势面之间关系、电势差与电场强度的关系,知道电势差与电场强度的定量关系。
主要素养与水平:科学推理(Ⅱ);科学论证(Ⅱ)。
5.参考解答:电子在匀强电场中做初速度为零的匀加速直线运动,根据动能定理:qU = \(\frac{1}{2}\)mv2 − \(\frac{1}{2}\)mv02;v0 = 0 可得 v = \(\sqrt {\frac{{2qU}}{m}} \) = \(\sqrt {\frac{{2 \times 1.6 \times {{10}^{ - 19}} \times 10}}{{9.1 \times {{10}^{ - 31}}}}} \) m/s = 1.87 × 106 m/s。
命题意图:会计算带电粒子在电场中沿直线运动的问题,亦可用本节正文介绍的动力学方法求速度。
主要素养与水平:能量观念(Ⅱ);科学论证(Ⅱ)。
资料链接
电场强度与电势差的定量关系
E = \(\frac{{{U_{AB}}}}{d}\) 仅适用于匀强电场,对于非匀强电场并不适用,但在极小空间范围内由于电场强度变化很小,可以近似看成匀强电场,此时上式可写成 E = − \(\frac{{\Delta \varphi }}{{\Delta l}}\)(Δφ 表示沿电场方向型距离上电势的变化量)。电场强度在任一方向的分量表示沿该方向电势变化率的负值。电场强度数值上等于沿电场线方向单位距离上降低的电势。负号的物理意义表示电场强度的方向与电势升高的方向相反。对三维情形,电场强度 E 与电势 φ 之间的关系为 E = − ∇φ(∇ 为梯度的符号),即电场强度大小与电势的梯度相等,方向相反。
发布时间:2022/5/19 下午1:57:58 阅读次数:9462
