第 5 节  带电粒子在电场中的运动  教学建议

1．教学目标

（1）会从运动和力的关系的角度、从功和能量变化的关系的角度分析带电粒子在匀强电场中的加速问题。

（2）知道带电粒子垂直于电场线进入匀强电场运动的特点，并能对偏移距离、偏转角度、离开电场时的速度等物理量进行分析与计算。

（3）了解示波管的工作原理，体会静电场知识对科学技术的影响。

（4）通过解决带电粒子在电场中加速和偏转的问题，加深对从牛顿运动定律和功能关系两个角度分析物体运动的认识，以及将匀变速直线运动分解为两个方向上的简单运动来处理的思路的认识。

2．教材分析与教学建议

在前面研究静电场性质的基础上，本节处理带电粒子在电场中运动的问题。本节内容由带电粒子在电场中的加速、带电粒子在电场中的偏转、示波管的原理三部分组成。教学内容的梯度适当，安排也符合学生的认知规律。其中示波管的原理为拓展学习内容，不仅对力学、电学知识的综合能力有较高的要求，而且要求有一定的空间想象能力。

本节教学的重点和难点是，围绕不同核心概念分析带电粒子的加速与偏转问题。这是因为，从运动和力的关系的角度、从功和能量变化的关系的角度分析问题的方法是解决问题的基础。由于力学与电学知识的综合应用程度逐渐提高，微观带电粒子的运动抽象，学生在学习这部分内容时常常会出现闲难。教师应该帮助学生设计适当的研究任务，铺设合理的台阶，引导学生交流讨论、解决问题，逐步提高他们的综合分析能力。

教科书是通过例题的形式来研究带电粒子的加速和偏转问题的。教学中应着重让学生掌握分析此类问题的思路，而不是死记硬背公式。

（1）问题引入

教科书本节课的“问题”栏目通过实际生活应用（医用电子直线加速器）激发学生探究加速原理。教学中可以为学生创设需要解决的真实问题情境，使学生产生求知欲望，用所学的知识、方法，自主展开研究活动。可以从现代科学实验和技术设备中选取典型实例，如环形加速器、示波器等。

（2）带电粒子在电场中的加速

此部分是牛顿运动定律和功能关系的综合运用。可利用教科书在旁批中提到的本章第 3 节例题用哪种思路的问题，让学生归纳解决加速问题的两种思路，明确利用能量观点解决问题的优点。例题 1 研究直线加速器，突出了实际应用性。学生对“电子在各个金属圆筒内做匀速直线运动”的理解会有困难，需要联系静电平衡知识。

教学片段

带电粒子在电场中的加速

问题：图 10–10 所示为直线加速器的示意图。平行金属板加上恒定电压 U，质量为 m、电荷量为 +q 的带电粒子从 A 板由静止释放。求粒子到达 B 板的速度大小。

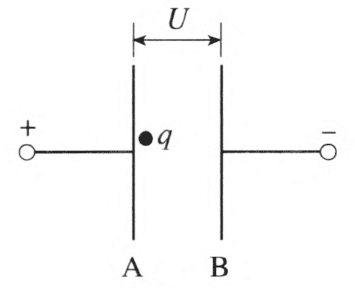
引导学生分别利用牛顿运动定律和动能定理求解：

（1）带电粒子在电场中做什么运动？

（2）设两板间的距离为 d，加速度为多大？

（3）粒子到达 B 板的速度为多大？

（4）静电力对带电粒子做的功为多大？

（5）粒子到达 B 板的动能为多大？速度为多大？

（6）解决带电粒子做匀加速运动问题的思路有哪些？应用动能定理有什么优越性？

（7）如果加速电场是非匀强电场，其他各量不变，粒子到达 B 板的动能为多大？速度为多大？

在处理带电粒子在电场中运动的问题时，通常重力可以忽略（本章第 3 节例题已提供了依据）。

（3）带电粒子在电场中的偏转

教科书图 10.5–2 给出了电子垂直电场线方向射入匀强电场的情景。为了强化学生的良好分析习惯，教师可以引导学生画出粒子初始时刻的初速度与受力图示，组织学生独立分析粒子的运动性质。由于静电力方向与电子的初速度方向垂直，且静电力是恒力，所以电子只能做匀变速曲线运动。这时让学生进一步思考：用什么方法分析处理此类曲线运动问题？促使学生联想到处理平抛运动的方法，提出把曲线运动分解为两个直线运动来处理。这样解决例题 2 就水到渠成了。例题 2 的教学中为突出用能量观点解决问题，可以引导学生求电子飞出电场的动能。

教学片段

例题 2 补充问题

①怎样求电子射出电场时的速度大小？

②组织交流：有几种方法求电子飞出电场时的速度大小？

③用动能定理求电子射出电场时的速度大小时，怎样求静电力做的功？

④比较利用牛顿运动定律和功能关系解决问题的不同点。

⑤请你谈谈电子偏转过程中能量的转化情况。

（4）示波管的原理

首先要认识示波管的结构，应该组织学生认真观察教科书图10.5-40示波管主要由电子枪、偏转电极和荧光屏三部分组成。电子枪通电后产生热电子，电子在加速电场作用下被加速的过程就是例题 1 讨论的情景。电子经过偏转电场的过程就是例题2讨论的情景，只是这里有两组偏转电极，使电子的运动轨迹变得更复杂。教学过程中可以设置有难度梯度的问题串，引导学生由浅入深地分步研究。组织学生根据问题串思考，并尝试描点画图、讨论与交流。首先需要明确：例题 2 中求得的垂直板面的侧向位移 y 的表达式说明，y 与偏转电压 U 成正比；因电子速度很大，穿越偏转电场的很短时间内，可以认为电压恒定不变。其次判断清楚只有一组电极间有电压时亮斑的位置。讨论电压变化引起电子位置变化时，采用从特殊到一般的分析顺序，即先描特殊点后连线。

教学片段

示波管的原理

设计思考与讨论问题：

①如果在电极 X、Xʹ 之间不加电压，但在 Y、Yʹ 之间加不变的电压，使 Y 的电势比 Yʹ 的高（有时说这种情况是“Y 正、Yʹ 负”），电子束运动过程中受哪个方向的力？电子将打在荧光屏的什么位置？试着在自制的图（在白纸上按教科书图 10.5–4  乙的样子画出荧光屏的放大图）中标出来。

如果在 Y、Yʹ 之间不加电压，而在 X、Xʹ 之间加不变的电压“X 正、Xʹ 负”，电子将打在荧光屏的什么位置？试着在教科书图 10.5–4 乙中标出来。

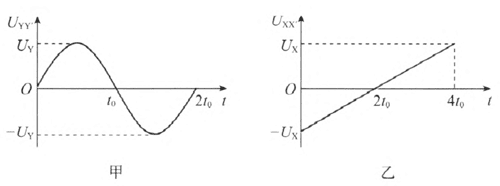
②如果在电极 X、Xʹ 之间不加电压，而在电极 Y、Yʹ 之间所加的电压按图 10–11 甲所示的规律随时间变化，在荧光屏上会看到什么图形？试着画出来。

③如果 Y、Yʹ 之间的电压仍然如图 10–11 甲所示，而在电极 X、Xʹ 之间加不变的电压“X 正、Xʹ 负”，在荧光屏上会看到什么图形？若 X、Xʹ 之间的电压是“X 负、Xʹ 正”呢？试着画出来。

④如果 Y、Yʹ 之间的电压仍然如图 10–11 甲所示，而在电极 X、Xʹ 之间所加的电压按图 10–11 乙所示的规律变化，在荧光屏上会看到什么图形？试着画出来。

“科学漫步”栏目中介绍了范德格拉夫静电加速器的工作原理，即利用尖端放电的原理起电，产生高电压，再用高电压对带电粒子加速。通过阅读可以使学生感悟到，使用这种加速器比使用放射性物质更加安全、更加环保。

3．“练习与应用”参考答案与提示

本节练习共 6 道题，既有知识运用训练，也有思想方法的提炼，还有理论联系实际的应用。第 1 题要求归纳该题的几种解法，比较这些解法哪种更简便。归纳和比较非常有意义，既可以开阔学生的思路，又可以使学生发现动能定理的优越性。第 2 题以光电效应实验作为背景，求电子的最大初速度。此题对运算的要求并不高，关键是要理解在什么条件下电流表会没有电流。本题通过分析电子的受力情况和运动情况，强化学生应用功能关系的意识，提高综合分析能力。第 3、4、5 题都是带电粒子在匀强电场中的偏转问题，其中第 4 题实质上是证明题。证明题使用的语言应该简洁、严密、逻辑性强，要对学生加强这方面的训练。第 6 题通过动能定理来研究带电粒子在电场中的运动，物理情景十分典型。

1．2.9×10⁻¹⁷ J

解法一：E_k = ΔE_k = W = qU = 2×1.6×10⁻¹⁹×90 J = 2.9×10⁻¹⁷ J。

解法二：E = \(\frac{U}{d}\)，E_k = ΔE_k = W = Eqd = \(\frac{U}{d}\)qd = qU = 2.9×10⁻¹⁷ J。

解法三：E = \(\frac{U}{d}\)，a = \(\frac{qE}{m}\)，v² = 2ad，E_k = \(\frac{1}{2}\)mv² = qU = 2.9×10⁻¹⁷ J。

可见，第一种解法最简单。

2．2.10×10⁶ m/s

提示：如果电子的动能减小到 0 的时候，电子恰好没有到达 N 板，则电流表中就没有电流。由动能定理得 W = − eU = 0 – E_km = − \(\frac{1}{2}\)m_ev²，解得 v = \(\sqrt {\frac{{2eU}}{{{m_{\rm{e}}}}}} \) = \(\sqrt {\frac{{2 \times 12.5 \times 1.6 \times {{10}^{ - 19}}}}{{0.91 \times {{10}^{ - 30}}}}} \) m/s = 2.10×10⁶ m/s。

3．（1）\(\frac{m_\rm{H}}{m+\rm{e}}\)；（2）1

提示：设加速电压为 U₀，偏转电压为 U，带电粒子的电荷量为 q，质量为 m，垂直进入偏转电场的速度为 v₀，偏转电场两极间距离为 d，极板长为 l，则带电粒子在加速电场中获得初动能 \(\frac{1}{2}\)mv₀² = qU₀，在偏转电场中的加速度 a = \(\frac{qE}{m}\)，在偏转电场中运动的时间 t = \(\frac{l}{v_0}\)。粒子离开偏转电场时，沿静电力方向的速度 v_y = at = \(\frac{qUl}{mdv_0}\)，速度方向的偏转角的正切 tanθ = \(\frac{v_y}{v_0}\) = \(\frac{qul}{mdv_0^2}\)。

（1）若电子与氢核的初速度相同，则 \(\frac{{\tan {\theta _{\rm{e}}}}}{{\tan {\theta _{\rm{H}}}}}\) = \(\frac{m_\rm{H}}{m+\rm{e}}\)。

（2）若电子与氢核的初动能相同，则 \(\frac{{\tan {\theta _{\rm{e}}}}}{{\tan {\theta _{\rm{H}}}}}\) = 1。

4．设加速电压为 U₀，偏转电压为 U，带电粒子的电荷量为 q，质量为 m，垂直进入偏转电场的速度为 v₀，偏转电场两极间距离为 d，极板长为 l，则粒子的初动能 \(\frac{1}{2}\)mv₀² = qU₀，粒子在偏转电场中的加速度 a = \(\frac{qU}{md}\)，在偏转电场中运动的时间 t = \(\frac{l}{v_0}\)。粒子离开偏转电场时，沿静电力方向的速度 v_y = at = \(\frac{qUl}{mdv_0}\)，速度方向的偏转角的正切 tanθ = \(\frac{v_y}{v_x}\) = \(\frac{qUl}{mdv_0^2}\)。粒子所带电荷量不同，其初动能就不同。但是把 mv₀² = 2qU₀ 代入偏转角的正切 tanθ = \(\frac{v_y}{v_0}\) = \(\frac{qUl}{mdv_0^2}\)，得 tanθ = \(\frac{{Ul}}{{2{U_0}d}}\)，可见粒子的偏转角度相同；粒子在静电力方向的偏转距离为 y = \(\frac{1}{2}\)at² = \(\frac{qUl^2}{2mdv_0^2}\) = \(\frac{{Ul*2}}{{4{U_0}d}}\)，可见粒子的偏转距离也相同，所以这些粒子不会分成三股。

5．1.9×10⁷ m/s．8.53°

提示：电子的初动能 \(\frac{1}{2}\)mv₀² = eU₀，v₀ = \(\sqrt {\frac{{2e{U_0}}}{m}} \)。垂直进入匀强电场后加速度 a = \(\frac{eU}{md}\)，在偏转电场中运动的时间 t = \(\frac{l}{v_0}\)。电子离开偏转电场时，沿静电力方向的速度 v_y = at = \(\frac{eUl}{mdv_0}\)。电子离开偏转电场时的速度方向的偏转角的正切 tanθ = \(\frac{v_y}{v_0}\) = \(\frac{eUl}{mdv_0^2}\) = \(\frac{{eUl}}{{2{U_0}de}}\) = \(\frac{{El}}{{2{U_0}}}\) = \(\frac{{5000 \times 0.06}}{{2 \times 1000}}\) = 0.15，v_y = v₀tanθ，v = \(\sqrt {v_y^2 + v_0^2} \) = v₀\(\sqrt {{{\tan }^2}\theta  + 1} \) = \(\sqrt {\frac{{2e{U_0}}}{m}({{\tan }^2}\theta  + 1)} \)。代入数值得 v = \(\sqrt {\frac{{2 \times 1.6 \times {{10}^{ - 19}} \times 1000}}{{9.1 \times {{10}^{ - 31}}}} \times (0.15 + 1)} \) m/s = 1.9×10⁷ m/s，θ = arctan0.15 = 8.53°。

6．1.30×10⁵ N/C

提示：由动能定理 Eql = \(\frac{1}{2}\)mv²，得 E = \(\frac{{m{v^2}}}{{2ql}}\) = \(\frac{{1.67 \times {{10}^{ - 27}} \times {{(1 \times {{10}^7})}^2}}}{{2 \times 1.6 \times {{10}^{ - 19}} \times 4.0}}\) N/C = 1.30×10⁵ N/C。