第三章 第二节 力的合成

图 3–19 港珠澳大桥
在日常生活中会遇到形式各异的桥梁,港珠澳大桥的“中国结·三地同心”主题斜拉索塔为研究力的合成提供了真实情境,结合本节主题将直观地理解力的合成的条件和意义。
本节的引入及第三节中的“STSE”均与此呼应。
本节编写思路
本节利用节首图和工程、生产中的实例引入共点力的概念,经历探究两个互成角度的力的合成规律实验,认识共点力的作用效果可被等效替代的事实。通过“大家谈”思考多个力合成的推理逻辑,感受从特殊到一般的思维方式。通过“学生实验”和“示例”掌握应用数形结合表示矢量合成的方法。
所经历的实验操作过程,对形成合作意识、培养实事求是的科学态度将起到积极的作用。
在日常生活中,经常会有多个力同时作用在同一个物体上的情形。图 3–19 和图 3–20 所示的场景中都有多根绳索,分别是斜拉桥上的钢索、起重机起吊钢材的钢缆、航天器返回舱降落伞的伞绳,每一根绳索上都有拉力作用。桥塔、钢材和返回舱都同时受到了多个不在同一直线上的力的作用,这些力作用于物体上同一点或力的作用线可以相交于同一点。这样的力称为共点力(concurrent force)。我们将从最基本的情况出发,分析两个互成角度的共点力的作用效果,进而理解多个力作用效果的分析方法。

(a)起重机用钢绳吊起钢材

(b)航天器返回舱和降落伞
图 3–20
两个人同时用力提起的箱子,大力士单手就能提起,那么这个大力士作用在箱子上的一个力的作用效果与两个人用两个力同时作用的效果是相同的。
教材通过生活实例引入合力、分力的概念以及等效替代的思想方法。合力与分力之间是“等效替代”的关系。
力的作用效果包括改变物体的运动状态,使物体产生形变。这里的“等效替代”主要是指用一个力替代原先几个力对物体的共同作用,物体呈现的运动状态或运动状态的改变相同。
对于力的形变效果来说,有时候几个力对物体的共同作用可以用一个力等效替代,有时则不能。如用两个大小相等、方向相反的力,沿水平方向分别拉放在光滑水平面上的橡皮筋的两端,使其产生伸长形变,就无法用一个力单独拉橡皮筋而使之产生同样的形变。但如果用一个力将橡皮筋一端固定在水平面上,另外两个力同时拉橡皮筋另一端,使橡皮筋伸长,就可换用另一个力来拉橡皮筋同一端,产生相同的形变效果。此时,可将作用于橡皮筋同一端的两个“分力”合成“合力”。等效替代是物理学研究问题的重要思想方法。在以后的学习中,如学习“运动的合成与分解”“等效电路”“交流电有效值的定义”等,都要用到“等效替代”的思想方法。
物体同时受到几个力的作用时,我们可以用一个力来替代这几个力,使这个力产生的效果与几个力同时作用的效果相同。这个力就称为合力(resultant force),而原来的几个力称为这个合力的分力(force components)。
求几个力的合力的方法称为力的合成(composition of forces)。
在初中已经学过同一直线上两个力的合成方法,下面我们通过实验来探究两个互成角度的共点力与它们的合力间有怎样的关系。
探究两个互成角度的力的合成规律
这是一个分组探究的学生实验。小猩猩双臂悬挂、受两个拉力作用与其单臂悬挂、受一个力作用,在运动状态上等效,从而提出探究两个“分力”与“合力”之间有何定量关系的问题。实际的实验探究则是橡皮筋一端固定,另一端受 1 个拉力(合力)和受 2 个拉力(分力)的效果相同。在学生分组实验探究得出两个“分力”与“合力”之间遵循平行四边形定则后,会产生两种不同的等效替代中“分力”与“合力”之间是否都遵循平行四边形定则的问题;该问题可通过实验进行探讨,即先用两个弹簧测力计(或力传感器)互成角度提起重物,然后再用一个弹簧测力计(或力传感器)提起同一重物;根据实验事实揭示拉橡皮筋和提重物两种情况中“分力”与“合力”之间都遵循平行四边形定则。
图 3–21 小猩猩将自己悬挂在树枝上
图 3–22 探究两个互成角度的力的合成规律的实验装置
提出问题
如图 3–21 所示,小猩猩用单臂或双臂都能将自己悬挂在树枝上。单臂上的力 F 与双臂上的两个力 F1、F2 的效果相同,F 是 F1、F2 的合力。F1 与 F2 的数值相加是否正好等于 F 的大小呢?
实验原理与方案
合力与两个分力同时作用的效果相同,可以互相替代。
测量各个力的大小与方向。
实验装置与方法
实验装置如图 3–22 所示。通过橡皮筋的形变量及形变方向来体现力的作用效果。
实验操作和数据收集
将橡皮筋的一端固定。两位同学合作,先同时用两个力 F1、F2 将橡皮筋的另一端拉
到某一点 O,同时记录 F1 和 F2 的大小和方向。再用一个力 F 将橡皮筋的端点拉到同一位置 O,记录 F 的大小和方向。
数据分析
过 O 点,按统一标度作出力 F1、F2 和 F 的图示。观察和分析它们的几何关系。
实验结论
两个共点力的合力可以用___________________________________表示。
交流与讨论
交流各组的实验结果,讨论合力是否一定比分力大。
实验表明:两个共点力 F1、F2 的合力 F 可以用以这两个力为邻边构成的平行四边形的对角线表示(图 3–23)。这就是力的平行四边形定则( parallelogram rule)。
图 3–21 中小猩猩双臂悬挂时受到的两个拉力的大小之和一般不等于单臂悬挂时所受的拉力,这三个力的关系遵循平行四边形定则。
平行四边形求和的方法适用于一切矢量的求和。我们学过的位移、速度、加速度也是矢量,它们的合成也遵循平行四边形定则求和的方法。图 1–7 中 A 到 C 的位移就是 A 到 B 与 B 到 C 位移的矢量和。
如何求三个共点力的合力?
通过“大家谈”,体验求两个以上共点力的合力的方法,深化对矢量求和遵循交换律、结合律的认识。
示例 两位学生同时用水平力推一个木箱使其沿直线移动,一位用力 300 N,另一位用力 400 N,两个水平推力的夹角是 90°,求这两个力的合力。
分析:首先需要判断这两个力是否为共点力。如果是共点力,可以根据平行四边形定则通过作图或代数运算求得结果。本题中的两个力为相互垂直的共点力,相应的平行四边形为矩形,除作图法外,还可以根据勾股定理求解。
解:方法一:
用作图法求合力,应注意:
(1)选择合适的统一标度,应使画出的代表两分力的矢量长度适中,不能太短;
(2)根据平行线的画法,用直尺和三角板尽可能准确地画平行四边形;
(3)对所画出的平行四边形的四条边和表示合力的对角线,实线、虚线要分清;
通过示范上述作图要点,培养认真细致的科学态度。
将木箱抽象为质点 O,如图 3–24 所示,选定 10 mm 长的线段表示 100 N 的力。作 F1 = 300 N、F2 = 400 N,F1 与 F2 相互垂直。
图 3–24 通过作图求合力
以 F1、 F2 为邻边作平行四边形,根据平行四边形定则,合力 F 为平行四边形的对角线。
用刻度尺量得对角线长为 50 mm,由此得到合力大小
\[F = \frac{{50\;{\rm{mm}}}}{{10\;{\rm{mm}}}} \times 100\;{\rm{N}} = 500\;{\rm{N}}\]
用量角器量出合力 F 与分力 F1 的夹角 α = 53°。
则合力 F 的大小为 500 N,合力的方向与 F1 的夹角为 53°。
方法二:
图 3–24 中 F1、F2 间夹角为 90°,由勾股定理可得
\[F = \sqrt {F_1^2 + F_2^2} = \sqrt {{{ (300\;{\rm{N}})}^2} + {{(400\;{\rm{N}})}^2}} = 500\;{\rm{N}}\]
由正切函数的定义可得
\[\tan \alpha = \frac{{{F_2 }}}{{{F_1}}} = \frac{{400\;{\rm{N}}}}{{300\;{\rm{N}}}} \approx 1.33,\alpha \approx 53^\circ \]
即合力 F 的大小为 500 N,合力的方向与 F1 的夹角为 53°。
- 如图 3–25 所示,三个物体均受到同一平面内三个力的作用。判断其中哪些属于共点力。
图 3–25
- 如图 3–26 所示,质点 O 受两个力的作用,通过作图求出图中两个已知力的合力。
图 3–26
- 力的合成遵循矢量运算法则,与标量的运算有什么不同?(可以用表格和图示等方法来对比说明)
- 大小为 3 N 和 5 N 的两个共点力同时作用在物体上,为什么它们的合力大小可能是 2 N、4 N 或 8 N,却不可能是 12 N?试用力的平行四边形定则来说明原因。
图 3–27
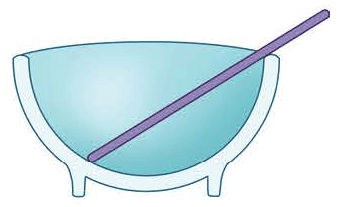
图 3–28
- 如图 3–27 所示,平面上有 5 个力作用在 O 点,O 点和各力的矢量终点恰好各位于一个正六边形的顶点,这 5 个力中最小的力是 1 N。先选择对称的力为分力作平行四边形来求 5 个力的合力;再以互相垂直的力为分力作平行四边形来求 5 个力的合力。比较两次的结果。
- 如图 3–28 所示,一根质量分布均匀的棒放在光滑的半球形碗内。棒受到三个力的作用,作出棒受到的重力与弹力的示意图。
问题与思考解读
1.参考解答:画出各个力的作用线,各力的作用线交于一点的即为共点力,如图所示。
命题意图:理解共点力,形成平面力系的概念。
主要素养与水平:科学推理(Ⅰ)。
2.参考解答:用一定长度的线段确定力的标度,根据规范的作图方法画出合力。
命题意图:规范作图,运用平行四边形定则求合力。
主要素养与水平:科学推理(Ⅰ)
3.参考解答:学生的表达至少要包含观点和证据,用文字、表格或图示均可。
命题意图:理解矢量和的代数、几何表示方法。
主要素养与水平:科学论证(Ⅰ)。
4.参考解答:3 N、4 N、5 N 构成勾三股四弦五。二力同向或反向时合力大小分别为 8 N 和 2 N,8 N 为合力的最大值,2 N 为合力的最小值。
命题意图:规范作图方法,体验数形结合。
主要素养与水平:科学推理(Ⅱ);科学态度(Ⅰ)。
5.参考解答:这 5 个力在同一平面内、且 F1 与 F2、F2 与 F3、F3 与 F4、F4 与 F5 之间的夹角均为 30°,按规范画出平行四边形,获得对角线,根据圆的性质得到合力的大小。两种方法得到的结果相同,合力大小为 6 N。
命题意图:规范地作图,与初中所学的圆、菱形和直角三角形知识构建联系。体会对称性。
主要素养与水平:科学推理(Ⅱ)。
6.参考解答:如图所示。
命题意图:由三个力是共点力这一前提出发画出力的示意图,以此感受和理解弹力的方向。进一步认识共点力(作用点不在一点上的共点力)。
主要素养与水平:运动与相互作用(Ⅰ);科学推理(Ⅰ)。
发布时间:2021/7/12 下午12:54:28 阅读次数:8818
