第 4 章 第 1 节 科学探究:力的合成
生活中常有这样的情境:两个人可将购物篮提起使其处于静止状态(图 4-1),一个人也可将这个购物篮提起使其处于同样状态,但这两种情形中手对购物篮的作用力不同。这些力之间有什么关系呢?本节将学习共点力的合成,通过实验探究共点力合成的规律。
|
图 4-1 提起的购物篮 |
1.共点力的合成
如果几个力同时作用在物体上的同一点,或它们的作用线相交于同一点,我们就把这几个力称为共点力(concurrent force)。当物体同时受到几个力的作用时,我们可用一个力来代替它们,且产生的作用效果相同。物理学中把这个力称为那几个力的合力(resultant force),那几个力则称为这个力的分力(component force)。求几个力的合力的过程称为力的合成(composition of forces)。在图 4-1 中, 两人对购物篮的作用力 F1 和 F2 是共点力。若由一个人提起购物篮,此时人对购物篮的作用力为 F。共点力 F1 和 F2 的作用效果与 F 的作用效果相同,因此 F 是 F1 和 F2 的合力,F1 和 F2 则是 F 的分力。
我们已学会了同一直线上两个力的合成。但是在很多情况下,作用在物体上的几个共点力互成角度,如图 4-1 中的 F1 和 F2。那么,力的合成遵循什么规律呢?
2.探究两个互成角度的力的合成规律
当作用在物体上的两个共点力不在一条直线上时,它们合力的大小是否等于两个分力大小之和或之差?这时的合力应该怎样确定?
实验目的
(1)探究两个互成角度的共点力与其合力间的关系。
(2)学习用等效的思想探究矢量合成的方法。
实验器材
木板、橡皮筋、细线、弹簧测力计、图钉、白纸、铅笔、刻度尺、三角板。
实验原理与设计
让两个互成角度的共点力 F1 和 F2 作用于某一物体,并产生明显的作用效果;然后用一个力 F 来代替 F1 和 F2,产生同样的作用效果。测出 F1、F2 和 F,比较它们的大小和方向,找出其中的规律。
实验步骤
(1)如图 4-2(a)所示,在铺有白纸的木板上,将橡皮筋一端用图钉固定于 A 点,另一端与两细线打一个结点 B。两细线分别挂上测力计。
(2)如图 4-2(b)所示,分别用力拉两只测力计,用铅笔标出结点 B 被拉伸到的位置,记为 O 点。记下此时两只测力计的示数 F1、F2,并沿两细线标记出力的方向。
(3)如图 4-2(c)所示,用力拉一只测力计,同样将结点 B 拉到 O 处,记下此时测力计的示数 F,并沿细线标记出力的方向。
(4)用力的图示画出 F1、F2 及 F。
图 4-2 探究共点力的合成
安全警示
不要将橡皮筋拉伸过长,小心放置图钉等,避免造成伤害。
数据分析
比较 F1、F2、F 的大小和方向,能否看出三者之间的关系?试一试,将 F1、F2、F 的箭头端用虚线连起来,能否找出规律并进行论证?
对比其他实验小组的数据,看一看你发现的规律是否具有普遍性。
实验结论
F 是 F1、F2 的合力,F1、F2 和 F 满足___________关系。
讨论
保持两只测力计的拉力大小不变,只改变它们的夹角,合力的大小如何变化?合力大小是否一定等于原来两个力的大小之和?合力是否一定大于原来的每一个力?请通过实验得出结论并说明原因。
素养提升
能观察实验现象,发现并提出物理问题,能作出初步的假设;能根据已有实验方案,使用弹簧测力计等器材收集数据;能通过图形分析,寻找规律,形成初步的结论,能与猜想进行比较;能参考教科书撰写有一定要求的实验报告,在报告中能呈现对实验数据的分析过程,知道交流的重要性。
注意提升提问能力、猜想假设能力及利用图像进行分析论证的能力。
——科学探究
3.平行四边形定则
大量实验研究表明,若以表示互成角度的两共点力的有向线段为邻边作平行四边形,则两邻边间的对角线所对应的这条有向线段就表示这两个共点力的合力大小和方向,如[图 4-3(a)]所示。这就是共点力合成所遵循的平行四边形定则(parallelogram rule)。
图 4-3 用平行四边形定则进行力的合成
实际上,物体所受的力常常不止两个。如果物体受到三个或更多个共点力的作用,我们可用平行四边形定则先求出其中两个力的合力,然后用平行四边形定则再求这个合力与第三个力的合力[图 4-3(b)],直到把所有外力都合成为止,最后得到这些力的合力。
前面已从有无方向的角度认识了矢量和标量。从运算角度来看,相加时遵循平行四边形定则的物理量称为矢量,如力、加速度等都是矢量;相加时遵循代数相加法则的物理量称为标量,如时间、路程等都是标量。矢量与标量遵循不同的运算法则,这是二者的重要区别。
拓展一步
用三角形定则求合力
由平行四边形定则可推出矢量合成的三角形定则。在求合力时,只要把表示原来两个力的有向线段首尾相接,然后从第一个力的始端向第二个力的末端画一条有向线段,这条有向线段就表示原来两个力的合力(图 4-4)。
如果物体受两个以上的力的作用,仍然可以用同样的作图法。把表示所有力的有向线段依次首尾相接,这样,从第一个力的始端向最后一个力的末端画出的有向线段就表示所有力的合力(图 4-5)。
图 4-4 两力的合成示意图
图 4-5 三力的合成示意图
例题
岸边两人同时用力拉小船,两力的大小和方向如图 4-6 所示。请分别用作图法和计算法求出这两个力的合力。

分析
已知两个共点力 F1、F2 的大小和方向,根据平行四边形定则,用力的图示法作平行四边形,那么,对角线对应的有向线段就表示这两个力的合力。
解
(1)作图法
选定合适的标度,如用 5.0 mm 长的线段表示 150 N 的力,用 O 点代表船。依据题意作出力的平行四边形,如图 4-7 所示。

用刻度尺量出表示合力 F 的对角线长为 20.0 mm,可求得合力的大小
\[F = 20.0 \times \frac{{150}}{{5.0}}{\rm{N}} = 600{\rm{N}}\]
用量角器量出 F 与 F1 的夹角为 60°。
故这两个力的合力大小为 600 N,方向与 F1 成 60°。
(2)计算法
如图 4-8 所示,平行四边形的对角线 AB、OD 交于 C 点,由于 OA = OB,所以平行四边形 OADB 是菱形,OD 与 AB 互相垂直平分,OD 是∠AOB 的角平分线,则

∠AOD = 60°,OD = 2OC = 2OA cos 60°
因此,合力的大小
\[F = 2{F_1}\cos 60^\circ = 600{\rm{N}}\]
方向与 F1 成 60°。
讨论
由计算可知,当两个力等大且夹角等于 120° 时,其合力与这两个力大小恰好相等。要使合力大于或小于这两个力,夹角需分别满足什么条件?
策略提炼
两个力的合力既可用作图法,又可通过计算求得。作图法直观明了,但在作图和测量时难免存在误差。相对而言,通过计算得到的结果更精确。在进行计算时,通常先作出平行四边形,再用三角函数等相关数学方法求解。选择用作图法还是通过计算求解,应根据题目的要求确定。
迁移
用计算法求合力,在画出平行四边形后,通常可用多种数学方法求解。上题还有其他计算方法吗?试试用更简单的方法求解。
物理聊吧
自制一个平行四边形模型(图 4-9),结合模型讨论以下问题:
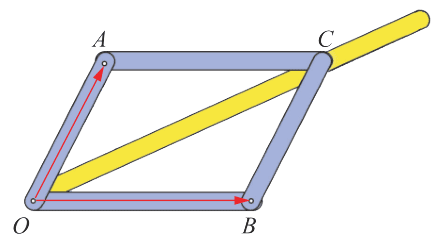
(1)合力的大小和方向怎样随两个分力夹角的改变而改变?
(2)合力是否总是大于两个分力?合力何时达到最大值,何时达到最小值?
(3)当两个分力之间的夹角分别为 0° 和180° 时,它们的合力如何计算?
说一说你的想法,并与同学交流。
节练习
1.请参考教科书内容撰写“探究两个互成角度的力的合成规律”的实验报告,注意在报告中呈现通过实验数据及力的图示得出初步结论的过程。
参考解答:略
2.在学过的物理量中,分别指出三个矢量和三个标量,并说出它们的运算规则。当几个矢量同在一条直线上时,它们的合成有什么特点?
参考解答:位移、速度、力等是矢量,其运算遵循平行四边形定则;时间、质量、路程等是标量,其运算遵循代数运算法则。当几个矢量同在一条直线上时,它们的合成仍然遵循平行四边形定则,可在规定正方向后用正负号表示矢量的方向,将矢量求和转化为代数运算,计算结果的正负表示合矢量的方向。
3.关于“探究两个互成角度的力的合成规律”的实验,下列说法正确的是
A.测合力时,橡皮筋的结点应被拉到测对应分力时的同一位置
B.实验中应尽量保持弹簧测力计的拉力方向与木板平行
C.实验中应保证两只弹簧测力计的拉力大小之和等于所测合力的大小
D.以两个力为邻边作平行四边形,两邻边间的对角线对应的有向线段表示合力的大小和方向
参考解答:ABD
4.若两个力大小分别为 F1 = 3 N、F2 = 8 N,则它们的合力大小可能为
A.1 N B.3 N C.10 N D.13 N
参考解答:C
5.作用在同一物体上的两个力的大小分别为 F1 = 20 N、F2 = 20 N。先用作图法求出两个力的夹角分别为 60°、90°、120° 时合力的大小和方向,再通过计算法求解。
参考解答:图略
34.6 N,方向与 F2 成 30°;28.3 N,方向与 F2 成 45°;20 N,方向与 F2 成 60°
6.三力的大小分别为 2 N、7 N、8 N,其夹角可变化。求它们合力的最大值和最小值。
参考解答:最小值为 0,最大值为 17 N
7.医生在治疗腿脚骨折时,常用如图所示的牵引方法。试算出图中伤腿所受的拉力。(取 sin 37° = 0.6,cos 37° = 0.8,重力加速度 g = 10 m/s2)
参考解答:80 N
发布时间:2022/3/30 下午5:18:56 阅读次数:4512

