第九章 第二节 电荷的相互作用 库仑定律

 

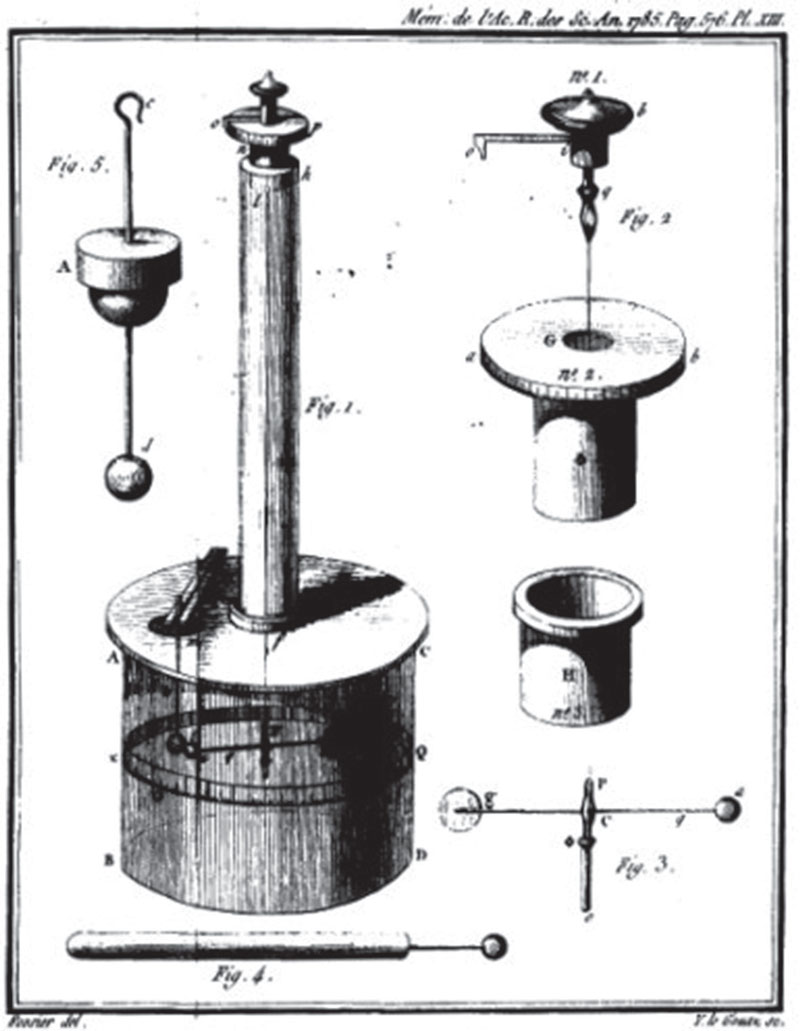
图 9–8   库仑扭秤实验装置图手稿

 

在如图 9–9 所示的场景中，将塑料丝的一半撕成细丝，用干燥的手掌握住塑料丝捋几下；塑料丝就会散开。我们在初中已经知道，电荷之间有相互作用，同号电荷间相互排斥、异号电荷间相互吸引。塑料丝散开正是因为手掌的摩擦在其上产生同号电荷相互排斥的结果。这种静止电荷之间的相互作用又叫做静电力。

如图 9–10 所示，把一个带正电的物体放在 M 处，然后把系在丝线上带正电的小球悬挂在 P 位置，小球拉动丝线发生偏转。改变 M 处带电体与小球之间的距离，观察偏角 θ 的变化；固定带电体的位置，改变其所带电荷量的大小，观察偏角 θ 的变化。带正电物体和小球间有静电排斥力作用，我们可以通过偏角 θ 的大小来定性判断小球受到的静电力的大小；偏角 θ 越大表示小球受到的静电力越大。

通过这样的实验，我们可初步知道电荷间相互作用力的大小与带电体间的距离有关，距离越小，作用力越大；静电力的大小还与两电荷的电荷量的大小有关，电荷量越大，作用力越大。

 

18 世纪中叶以前，研究带电体之间的静电力遇到三大困难：一是任意带电体上的电荷分布难以确定，无法确定相互作用的电荷间的距离；二是这种静电力非常小，没有测量如此小力的工具；三是当时还没有度量电荷量的单位，也就无法确定电荷量的大小。

法国物理学家库仑（C. A. de Coulomb，1736—1806）巧妙地解决了这些困难。他根据电荷在金属球表面上均匀分布的特点，把金属球上的电荷想象成集中在球心的“ 点电荷”。这一模型就解决了测量带电体之间距离的问题。

 

库仑设计制作了一台能够测出微弱作用力的扭秤，用以测量两个同种点电荷之间的作用力，如图 9–8 所示就是他当时的手稿。装置主要结构如图 9–11 所示。库仑从牛顿的万有引力规律得到启发，用类比的方法来研究电荷间的相互作用。

如图 9–11 所示，库仑扭秤固定装置中有一根弹性扭丝（细金属丝、石英玻璃丝等），它的一端固定在一个旋转螺丝上；另一端连接绝缘棒的中点，使绝缘棒水平悬挂在扭丝上。绝缘棒的一端有一个金属小球 A，另一端是一个质量大小相同的金属小球 B。在离 A 不远处放一个跟 A 相同的金属球 C。当弹性扭丝处于自然状态时，调节螺丝使 A 与 C 接触；接着使 C 带电，则 A、C 带同号电荷，它们之间的斥力使绝缘棒发生转动，扭丝扭转，使得绝缘棒重新平衡。根据扭丝的扭转角 θ 与使扭丝扭转的力 F 成正比的规律就可以找出电荷间的相互作用力跟距离的关系。

 

 

库仑用扭秤进行实验，通过和万有引力的类比较快得出了电荷间作用力 F 跟距离 r 的二次方成反比 \(\left( {F \propto \frac{1}{{{r^2}}}} \right)\) 的规律。如仅靠实验数据的积累，也许这个规律的发现可能会被推迟。

电荷间的相互作用力一定和电荷量有关。库仑细心地发现两个相同的带电金属球相互接触后，它们对相同距离外的第三个带电小球的作用力相等，所以他断定这两个小球所带的电荷量相等。利用了电荷在两个相同金属球之间等量分配的原理，可把带电小球的电荷量 q 分为 \(\frac{q}{2}\)，\(\frac{q}{4}\)，\(\frac{q}{8}\)，…这样就保证了实验中金属球的电荷量成倍变化。

从而，库仑发现了电荷间的相互作用力 F 与电荷量 q 的关系，即 F 与电荷量 q₁、q₂ 的乘积成正比（F ∝ q₁q₂）。

综上可得，F ∝ \(\frac{{{q_1}{q_2}}}{{{r^2}}}\)。

---

 

真空中两个静止的点电荷之间相互作用力的大小跟它们的电荷量的乘积成正比，跟它们之间的距离的二次方成反比，作用力的方向在它们的连线上。这叫做库仑定律（Coulomb’s law），可用下面的公式表示

\[\color{#975F85}{F = k\frac{{{q_1}{q_2}}}{{{r^2}}}}\]

电荷间的这种相互作用的静电力又称为库仑力。式中 k 叫做静电力常量，在国际单位制中，k = 9×10⁹ N·m²/C²。就是说，两个均带 1 C 电荷量的点电荷即使在相距 1 m 的情况下，它们相互间的库仑力依然高达 9×10⁹ N，可见库仑（C）是个很大的电荷量单位。

 

示例 1  如图 9–12 所示，真空中有两个点电荷 q₁ 和 q₂，它们的电荷量分别是 + 4.0×10⁻⁹ C 和 − 2.0×10⁻⁹ C，两点电荷间相距 10 cm，求这两个点电荷间的相互作用力。（已知静电力常量 k = 9×10⁹ N·m²/C²）

分析：在运用库仑定律时，物理量都要采用国际单位制；点电荷的电荷量可用绝对值代入，这样可以避免因对正、负号意义混淆不清而造成错误；库仑力的方向可以通过同号电荷相互排斥、异号电荷相互吸引来直接判断。

解：以电荷 q₂ 为研究对象，q₂ 受到 q₁ 对其的静电力作用，根据库仑定律，q₁ 对 q₂ 的静电力的大小

\[\begin{array}{l}{F_{12}} = k\frac{{\left| {{q_1}} \right|\cdot\left| {{q_2}} \right|}}{{{r^2}}}\\ \;\;\;\;\;= 9 \times {10^9} \times \frac{{4 \times {{10}^{ - 9}} \times 2.0 \times {{10}^{ - 9}}}}{{{{(0.10)}^2}}}\;{\rm{N}}\\ \;\;\;\;\;= 7.2 \times {10^{ - 6}}\;{\rm{N}}\end{array}\]

方向为沿 q₁、q₂ 连线指向 q₁。

同理，以电荷 q₁ 为研究对象，根据库仑定律，可得 q₂ 对 q₁ 的静电力 F₂₁ 与 q₁ 对 q₂ 的静电力 F₁₂ 大小相等、方向相反、作用在同一直线上。因此 F₂₁ 大小也为 7.2×10⁻⁶ N，方向为沿 q₁、q₂ 连线指向 q₂。

 

示例 2  已知氢原子中质子的质量为 m₁ = 1.67×10⁻²⁷ kg，电子的质量为 m₂ = 9.1×10⁻³¹ kg，在氢原子内质子和电子间的距离为 r = 5.3×10⁻¹¹ m，求氢原子中质子与电子之间的库仑力和万有引力大小的比值。（已知引力常量 G = 6.67×10⁻¹¹ N·m²/kg²，静电力常量 k = 9×10⁹ N·m²/C²，元电荷 e = 1.6×10⁻¹⁹ C）

分析：氢原子内质子和电子间距离为 5.3×10⁻¹¹ m。当代物理学认为氢核即质子，其直径在 10⁻¹⁵ m 量级，而电子直径则在 10⁻¹⁸ m 量级，两带电体间距离远大于带电体的直径，故质子和电子均可看成质点和点电荷。它们间的相互作用符合万有引力和库仑定律的适用范围。

 

解：设质子和电子间的库仑力为 F₁，万有引力为 F₂，质子所带电荷量为 q₁，电子所带电荷量为 q₂，则由库仑定律和万有引力定律

\({F_1} = k\frac{{{q_1}{q_2}}}{{{r^2}}}\)，\({F_2} = G\frac{{{m_1}{m_2}}}{{{r^2}}}\)

可得彼此间的库仑力和万有引力大小之比为

\[\begin{array}{l}\frac{{{F_1}}}{{{F_2}}} = \frac{{k\left| {{q_1}} \right| \cdot \left| {{q_2}} \right|}}{{G{m_1}{m_2}}}\\ \;\;\;\;\;= \frac{{9.0 \times {{10}^9} \times 1.6 \times {{10}^{ - 19}} \times 1.6 \times {{10}^{ - 19}}}}{{6.67 \times {{10}^{ - 11}} \times 1.67 \times {{10}^{ - 27}} \times 9.1 \times {{10}^{ - 31}}}}\\ \;\;\;\;\;\approx 2.3 \times {10^{39}}\end{array}\]

本节编写思路

本节通过带同号电荷塑料丝的相互排斥现象，引出静止电荷之间存在着静电力的概念。先定性探究静电力的大小由哪些因素决定，知道电荷间相互作用力与带电体间的距离和两电荷的电荷量大小有关。然后体验在研究带电体之间相互作用力的定量关系时，如何解决遇到的三大困难：一是相互作用的电荷间距离的确定；二是微小库仑力测量问题；三是电荷量测量问题。通过静电力和万有引力的对比，体会自然规律的多样性和统一性。最后通过具体实例知道利用电荷之间的相互作用规律处理复杂带电体之间的静电力作用的思想和方法。

通过学习静电力与电荷之间距离的二次方成反比的过程中所涉及的类比、模型建构、守恒和对称、微小量放大等方法，体验科学思维方法在科学研究中的重要作用。通过实验探究引导学生学习物理学的研究方法，渗透科学本质观的教育。了解科学家如何巧妙解决实验过程中的诸多问题，培养学生的科学态度和责任素养。

正文解读

通过节首图库仑定律实验装置手稿照片，启发学生体会库仑扭秤实验装置（图 9–8 中 Fig 1）设计中的一些细节（图 9– 8 中 Fig 2 ~ 5），了解科学家在探究库仑定律过程中是如何巧妙解决电荷量测量、微小库仑力测量等实验过程中的许多问题的。

本节第 8 页的图 9 – 11 和“拓展视野”的内容与节首图相呼应。

 

用演示实验定性探究影响静电力大小的因素，知道电荷间相互作用力与带电体间的距离和两电荷的电荷量大小有关。实验时应注意尽可能使带电体与系在丝线上的带电小球静止后处于同一高度。

 

此处设置“大家谈”的目的是让学生体验类比法在科学研究中的作用，以便以后在其他场合也能尝试运用建立理想化模型的方法研究物理问题。

在研究物体的运动时，如仅研究物体整体的平动，或者所涉及的空间尺度比物体自身的尺度大得多时，可以不考虑物体的大小和形状，把它简化为质点。在研究电荷间相互作用力的规律时，如所涉及的带电体的尺度比它们之间的距离小得多时，我们也可以把带电体抽象成只有电荷量没有大小的点，即点电荷。实际上任何带电体都有其大小和形状，真正的点电荷是不存在的。

 

法国物理学家库仑于 1785 年发表了一篇有关电荷间作用力的论文，其中提出如节首图 9 – 8 手稿所示的扭秤实验装置，在管顶有螺旋测角器，下面用弹性扭丝悬挂一横杆，玻璃缸壁上刻有 360 个刻度，可以读数。弹性扭丝处于自由状态时，横杆上的小球 A 指在零刻度。固定在绝缘竖杆末端的小球 C，带电以后通过玻璃盖板上的洞放入缸内，与大小相同的小球 A 接触后分开，这样 A、C 两球带上等量同号电荷而相互排斥。然后旋转管顶的旋转螺丝使两球恢复到初始位置，可从管顶的螺旋测角器读出弹性扭丝的扭转角 θ。根据扭丝的扭转角 θ 和两带电体之间距离 r 的关系，得出“带同号电荷的两球之间的排斥力与两球中心之间的距离的二次方成反比”的结论。后来库仑又通过电引力扭摆实验（详见本节资料链接）进一步证明了异号电荷间存在的吸引力也满足二次方反比的关系，总结出了库仑定律，并测出了静电力常量。

库仑定律是电学发展史上的第一个定量规律，是电磁学和电磁场理论的基本定律之一。电荷量的单位就是为了纪念库仑而以他的名字命名的。

 

此处设置“拓展视野”，旨在为课程标准 3.1.2 中明确提出的“体会探究库仑定律过程中的科学思想和方法”提供史料。

介绍库仑扭秤实验用弹性扭丝的扭转角间接测量静电力变化的比值关系的巧妙测量方法，目的是希望学生可试着根据弹性扭丝的扭转角 θ 与带电体之间距离 r 的实验数据，探究得到扭转角 θ 与距离 r 的二次方成反比（θ ∝ \(\frac{1}{{{r^2}}}\)）的结论。此实验中用到扭力和力矩平衡的知识，学生此前并没有学过，课程标准中也没有相应的要求，可对学有余力的同学课后补充讲解。由于库仑扭秤实验结构上的复杂性和操作上的精确性，这里并不要求学生熟悉实验器材、掌握实验操作步骤，而是侧重介绍库仑扭秤实验的设计思路与其中包含的科学思想和方法。

得出扭转角 θ 与距离 r 的二次方成反比（θ ∝ \(\frac{1}{{{r^2}}}\)）后，再根据 F ∝ θ，即得 F ∝ \(\frac{1}{{{r^2}}}\)，可和联想到的同样与距离二次方成反比的万有引力类比。

 

此处设置“助一臂”，是为了展现库仑定律发现的历史背景，突显类比的方法在库仑定律发现过程中所起的作用，体会物理学的和谐统一之美，提高学生学习物理的兴趣。

 

教学中，建议此处呵让学生根据库仑定律表达式导出静电力常量的单位，从而理解静电力常量是的单位是由公式中 F、q、r 的单位确定的，而它们在国际单位制中的单位是牛（N）、库（C）、米（m）。进而理解使用此常量 k = 9.0 × 10⁹ N·m²/C² 根据库仑定律计算时，只在国际单位制下才成立。

在真空中静电力常量 k 也常常写成 k = \(\frac{1}{{4\pi {\varepsilon _0}}}\) 的形式，ε₀ 是物理学中的一个基本物理常量，叫做真空介电常数或真空电容率。ε₀ = 8.9 × 10⁻¹² C²/N·m²。引入 ε₀ 后，库仑定律可改写为

\[F = \frac{1}{{4\pi {\varepsilon _0}}} \cdot \frac{{{q_1}{q_2}}}{{{r^2}}}\]

 

此处设置“大家谈”的目的是通过静电力与万有引力的对比体会自然规律的多样性和统一性（与距离的二次方成反比）。通过示例 2 体会微观带电粒子间的相互作用中，静电力的大小远大于万有引力的大小，为后续章节研究带电粒子在电场中的运动时忽略重力对带电粒子的影响做铺垫。静电力可以是相互吸引或相互排斥的，而万有引力一定是彼此相互吸引的。

带电粒子间的静电力和万有引力在大小、方向、表达式上的异同：

① 大小：通过示例 2 可见微观粒子间的万有引力远小于静电力。因此在研究微观带电粒子的相互作用时，往往可以忽略万有引力。

② 方向：万有引力都是吸引力，而静电力可以是吸引力，也可以是排斥力。

③ 表达式：库仑定律和万有引力定律数学表达式很类似，都遵从二次方反比规律；都是跟相互作用的两个物体有关，前者跟它们的电荷量有关，后者跟它们的质量有关，并且都成正比。

④ 作用力的方向均沿着两物体（质点、点电荷）间的连线。

问题与思考解读

1．参考解答：① 类比（库仑力与万有引力类比）  ② 模型建构（把金属带电球体建构为点电荷）  ③ 守恒和对称思想（两相同金属球接触后电荷量均分）  ④ 微小量放大（库仑扭秤实验）

命题意图：总结本节内容中的科学研究方法，体会科学思想。

主要素养与水平：科学态度（Ⅰ）。

 

2．参考解答：真空中的两个点电荷，相距为 r 时相互作用的静电力大小为 F，根据库仑定律 F = k \(\frac{{{q_1}{q_2}}}{{{r^2}}}\)；若将这两个点电荷的电荷量减半的同时距离变为 2r，则它们之间的静电力大小变为 F′ = k \(\frac{{\frac{1}{2}{q_1} \cdot \frac{1}{2}{q_1}}}{{{{(2r)}^2}}}\) = \(\frac{1}{16}\)F。

命题意图：运用库仑定律解决问题，加深对库仑定律相关概念的理解。

主要素养与水平：运动与相互作用观念（Ⅰ）。

 

3．参考解答：

（1）F = k \(\frac{{\left| {{q_1}} \right| \cdot \left| {{q_2}} \right|}}{{{r^2}}}\) = 9×10⁹ × \(\frac{{2.0 \times {{10}^{ - 6}} \times 4.0 \times {{10}^{ - 6}}}}{{{{0.2}^2}}}\) N = 18 N

（2）如需计算带电小球的质量 m，我们还需测量细绳与竖直方向的夹角 θ，根据共点力平衡可得：F = mgtanθ，θ 为带电小球悬绳的偏角，从而计算得到带电小球的质量。

命题意图：将静电知识与力学知识相关联，培养学生综合分析问题和解决问题的能力。

主要素养与水平：运动与相互作用观念（Ⅱ）；证据（Ⅱ）；解释（Ⅰ）。

 

4．参考解答：F = k \(\frac{{{q_1}{q_2}}}{{{r^2}}}\) = k \(\frac{{{e^2}}}{{{{(\sqrt 2 d)}^2}}}\) = 9×10⁹ × \(\frac{{{{(1.6 \times {{10}^{ - 19}})}^2}}}{{2 \times {{(2.82 \times {{10}^{ - 10}})}^2}}}\) N = 1.45 × 10⁻⁹ N

命题意图：运用概念和规律解答实际问题。

主要素养与水平：运动与相互作用观念（Ⅱ）；模型建构（Ⅱ）；科学推理（Ⅱ）。

 

5．参考解答：以地球为研究对象，仅受到万有引力和静电力的作用。万有引力 F_引 和静电力 F_静 二力平衡：F_引 = F_静，可得 G \(\frac{{{m_1}{m_2}}}{{{r^2}}}\) = k \(\frac{{{Q^2}}}{{{r^2}}}\)，即 Q = \(\sqrt {\frac{{G{m_1}{m_2}}}{k}} \) = \(\sqrt {\frac{{6.67 \times {{10}^{ - 27}} \times 6.0 \times {{10}^{24}} \times 7.3 \times {{10}^{22}}}}{{9 \times {{10}^9}}}} \) C = 5.7 × 10¹³ C。又因为 Q = Ne，所以所需氢离子总数N = \(\frac{{2Q}}{e}\) = \(\frac{{2 \times 5.7 \times {{10}^{13}}}}{{1.6 \times {{10}^{ - 19}}}}\) = 7.125 × 10³² 个。氢离子物质的量 n = \(\frac{N}{{{N_A}}}\) = \(\frac{{7.125 \times {{10}^{32}}}}{{6.02 \times {{10}^{23}}}}\) mol = 1.18 × 10⁹ mol，氢离子质量 m = nM = 1.18 × 10⁹ × 1 g = 1.18 × 10⁶ kg。

命题意图：通过一个假设的情境，模型建构后进行科学推理，体会相互作用观念。

主要素养与水平：运动与相互作用观念（Ⅱ）；科学推理（Ⅲ）；科学论证（Ⅲ）。

资料链接

电引力扭摆实验

库仑利用扭秤研究了同号电荷间的斥力。但在异号电荷间扭秤的引力研究中，由于金属扭丝扭转的恢复力矩仅与角度的一次方成比例，不能保证扭秤的稳定，两带电球如果相距较远，则其误差很大；如果相距较近，由于扭秤十分灵活，两球会出现左右摇摆相碰的现象。两球相互吸引的结果常常是相互接触而发生电荷中和现象，使实验无法进行下去。库仑把电荷间的吸引力和地球对物体的万有引力加以类比，从单摆受地球万有引力而摆动的事实受到启发。在地球对物体作用力遵从二次方反比规律的前提下，必然存在地面上的单摆摆动周期正比于摆锤离地心的距离。库仑认为电荷间的吸引力也应与此相近。

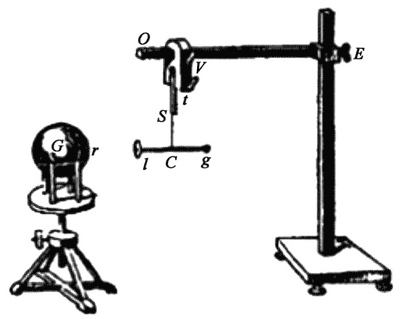
《物理学原著选读》一书记载的库仑电摆实验如图 7 所示，G 是一个直径为 1 英尺（0.304 8 m）的铜球或锡包的纸板球，由四根涂有西班牙蜡的玻璃直柱撑起，直柱下端，与四根三英寸或四英寸长的西班牙蜡棍端接，使该玻璃直柱更为绝缘。各玻璃柱的下端有个基底，放在可以活动的小桌上，在其旁边用一根从茧中抽出的长 7 ~ 8英寸（17.78 ~ 20.32 cm）的单根蚕丝 SC，将虫漆制成的针 lg 吊起，在 l 端装一个用金箔剪成的、直径 0.8 英寸（2.032 cm）的圆形小金箔，与针垂直，丝线悬于火炉烧干的、涂有虫漆或西班牙蜡的小铁杆 St 下端的 S 处，该铁杆由一个可以沿刻度尺 OE 滑动的钳夹住在 t 处，滑尺 OE 可由螺旋 E 来调整其高度，并可由螺旋 V 使其位于任何所需的位置。实验时，使 G 和 l 带异号电荷，则小针受引力摆动，测量出 G、l 在不同距离时，针堙摆动同样次数的时间，从而计算出每次的振动周期。

库仑记录了三次实验数据如下表所示：

实验序号	金箔与球心距离（英寸）	15 次振动所需时间（s）
1	9	20
2	18	41
3	24	60

三次实验中，金箔与球心距离之比为 3∶6∶8，假如电摆的周期与金箔到金属球球心距离成正比，则根据理论它们的周期之比应为 20∶40∶53.33，但是实验测得值为 20∶41∶60。库仑认为实际测得的时间与理论时间不同的原因是漏电。