3.3 库仑定律的发现

库仑定律是电磁学的基本定律之一，发现于 1785 年。它是继牛顿引力定律之后的第二个作用力与距离平方成反比的物理规律，两个规律有相似性。人们利用引力和电力或磁力的相似性用类比方法进行推测，对库仑定律的发现起到了借鉴作用，但是如果没有实验的检验，仅仅是理论上的推测，再聪明的头脑也无法作出决断。库仑定律的发现过程正说明了这一点。

3.3.1 从万有引力得到的启示

18 世纪中叶，牛顿力学已经取得辉煌胜利，人们借助于已经确立的万有引力定律，对电力和磁力的规律作了种种猜测。

德国柏林科学院院士爱皮努斯（F.U.T.Aepinus，1724—1802）1759 年对电力作了研究。他在书中假设电荷之间的斥力和吸力随带电物体的距离的减少而增大，于是对静电感应现象作出了更完善的解释。不过，他并没有实际测量电荷间的作用力，因而只是一种猜测。

1760 年，D.伯努利首先猜测电力会不会也跟万有引力一样，服从平方反比定律。他的想法显然有一定的代表性，因为平方反比定律在牛顿的形而上学自然观中是很自然的观念，如果不是平方反比，牛顿力学的空间概念就要重新修改。[1]

富兰克林的空罐实验（也叫冰桶实验）对电力规律有重要启示。1755 年，他在给兰宁（John Lining）的信中，提到过这样的实验：

“我把一只品脱银罐放在电支架（按；即绝缘支架）上，使它带电，用丝线吊着一个直径约为 1 英寸的木椭球，放进银罐中，直到触及罐的底部，但是，当取出时，却没有发现接触使它带电，像从外部接触的那样。”[2]

富兰克林的这封信不久跟其他有关天电和尖端放电等问题的信件，被人们整理公开发表，流传甚广，很多人都知道这个空罐实验，不过也和富兰克林一样，不知如何解释这一实验现象。富兰克林有一位英国友人，名叫普利斯特利（Joseph Priestley，1733—1804），是化学家，对电学也很有研究。富兰克林写信告诉他这个实验并向他求教。普利斯特利专门重复了这个实验，在 1767 年的《电学历史和现状及其原始实验》一书中他写道：

“难道我们就不可以从这个实验得出结论：电的吸引与万有引力服从同一定律，即距离的平方，因为很容易证明，假如地球是一个球壳，在壳内的物体受到一边的吸引作用，决不会大于另一边的吸引。”[3]

普利斯特利的这一结论不是凭空想出来的，因为牛顿早在 1687 年就证明过，如果万有引力服从平方反比定律，则均匀的物质球壳对壳内物体应无作用。他在《自然哲学的数学原理》第一篇第 12 章《球体的吸力》一开头提出的命题，内容是：“设对球面上每个点都有相等的向心力，随距离的平方减小，在球面内的粒子将不会被这些力吸引。”

牛顿用图 3 – 13 作出证明，他写道：

“设 HIKL 为该球面，P 为置于其中的一粒子，经 P 作两根线 HK 和 IL，截出两段甚小的弧 HI，KL；由于三角形 HPI 与 LPK 是相似的，所以这一段弧正比于距离HP，LP；球面上任何在 HI 和 KL 的粒子，终止于经过 P 的直线，将随这些距离的平方而定[4]。所以这些粒子对物体 P 的力彼此相等。因为力的方向指向粒子，并与距离的平方成反比。而这两个比例相等，为 1∶1。因此引力相等而作用在相反的方向，互相破坏。根据同样的理由，整个球面的所有吸引力都被对方的吸引力推动。证毕。”[5]

牛顿的论述在当时是众所周知的。读过牛顿著作的人都有可能推想到，凡是遵守平方反比定律的物理量都应遵守这一论断。换句话说，凡是表现这种特性的作用力都应服从平方反比定律。这就是普利斯特利从牛顿著作中得到的启示。

不过，普利斯特利的结论并没有得到科学界的普遍重视，因为他并没有特别明确地进行论证，仍然停留在猜测的阶段，一直拖了 18 年，才由库仑（Charles Augustin Coulomb，1736—1806）得出明确的结论。

在这中间有两个人曾作过定量的实验研究，并得到同样的结果。可惜，都因没有及时发表而未对科学的发展起到应有的推动作用。

一位是罗比逊（John Robison）。1769 年，他注意到爱皮努斯那本用拉丁文写的书，对爱皮努斯的猜测很感兴趣，就设计了一个转臂装置（如图 3 – 14），转臂的一端有一带电球，与附近另一相同的带电球相互有静电力作用。转臂实际上是一可活动的杠杆，调节杠杆支架的角度，就可以改变电力的力矩和重力的力矩，使之达到平衡，然后从支架的平衡角度，可以推算出电力与距离的关系。他先是把电力 f 与两球距离 r 的关系用公式 f = \(\frac{1}{{{2^{2 + \delta }}}}\) 表示，然后根据实验结果推算得 δ = 0.06。这个 δ 就叫指数偏差。他说，他做了“数百次的”这类测量，彼此相符“远远超过了预期”。罗比逊认为，指数偏大的原因应归于实验误差，由此得出结论，“带电球的作用力正好相当于球心之间距离的反平方”[6]，如爱皮努斯的推测一样。不过，他的实验结果仅限于同号电的斥力。至于异号电的吸力，他的装置显然难以胜任，他也没有留下明确的文字记载。有资料说，罗比逊得到异号电的吸力是指数略小于 2，因此平均取 2 次幂，从而得到电力反比于距离平方的结论，看来依据不足。罗比逊的论文在 1822 年才发表，这时库仑的工作早已得到公认。

另一位是卡文迪什（Henry Cavendish，1731—1810）。他在 1773 年用两个同心金属壳作实验，如图 3 – 15 所示。外球壳由两个半球装置而成，两半球合起来正好形成内球的同心球。卡文迪什这样描述他的装置：

“我取一个直径为 12.1 英寸的球，用一根实心的玻璃棒穿过中心当作轴，并覆盖以封蜡。……然后把这个球封在两个中空的半球中间，半球直径为 13.3 英寸，\(\frac{1}{20}\) 英寸厚。……然后，我用一根导线将莱顿瓶的正极接到半球，使半球带电。”[7]

卡文迪什通过一根导线将内外球连在一起，外球壳带电后，取走导线，打开外球壳，用木髓球验电器试验内球是否带电。结果发现木髓球验电器没有指示，证明内球没有带电，电荷完全分布在外球上。

卡文迪什将这个实验重复了多次，确定电力服从平方反比定律，指数偏差不超过 0.02。卡文迪什这个实验的设计相当巧妙。他用的是当年最原始的电测仪器，却获得了相当可靠而且精确的结果。他成功的关键在于掌握了牛顿万有引力定律这一理论武器，通过数学处理，将直接测量变为间接测量，并且用上了示零法精确地判断结果，从而得到了电力的平方反比定律。

卡文迪什为什么要做这个实验呢？话还要从牛顿那里说起。

牛顿在研究万有引力的同时，还对自然界其他的力感兴趣。他把当时已知的三种力重力、磁力和电力放在一起考虑，认为都是在可感觉的距离内作用的力，他称之为长程力（long-range force）。他企图找到另外两种力的规律，但都未能如愿。磁力实验的结果不够精确。他在《原理》的第三篇中写道：

“引力的性质与磁力不同；因为磁力并不正比于被吸引的物质。某些物体受磁石吸引较强；另一些较弱；而大多数物体则完全不被磁石吸引。同一个物体的磁力可以增强或减弱；而且远离磁石时它不正比于距离的平方而是几乎正比于距离的立方减小，我这个判断得自较粗略的观察”。[8]

至于电力，他也做过实验，但带电的纸片运动太不规则，很难显示电力的性质。

在长程力之外，他认为还有另一种力，叫短程力（short-range force）。他在做光学实验时，就想找到光和物质之间的作用力（短程力）的规律，没有实现。他甚至认为还有一些其他的短程力，相当于诸如聚合、发酵等现象。

3.3.2 卡文迪什和米切尔的工作

牛顿的思想在卡文迪什和另一位英国科学家米切尔的活动中得到了体现。米切尔是天文学家，也对牛顿的力学感兴趣。在 1751 年发表的短文《论人工磁铁》中，他写道：

“每一磁极吸引或排斥，在每个方向，在相等距离其吸力或斥力都精确相等……按磁极的距离的平方的增加而减少，”他还说：“这一结论是从我自己做的和我看到别人做的一些实验推出来的。……但我不敢确定就是这样，我还没有做足够的实验，还不足以精确地做出定论。”[9]

既然实验的根据不足，为什么还肯定磁力是按距离的平方成反比地减少呢？甚至这个距离还明确地规定是磁极的距离，可是磁极的位置又是如何确定的呢？显然，是因为米切尔面前摆着平方反比规律的先例。

在米切尔之前确有许多人步牛顿的后尘研究磁力的规律，例如；哈雷（1687 年）、豪克斯比、马森布洛克等人都做过这方面的工作，几乎连绵百余年，但都没有取得判决性的结果。米切尔推断磁力平方反比定律的结论可以说是牛顿长程力思想的胜利，把引力和磁力归于同一形式，促使人们更积极地去思考电力的规律性。

米切尔和卡文迪什都是英国剑桥大学的成员，在他们中间有深厚的友谊和共同的信念。米切尔得知库仑发明扭秤后，曾建议卡文迪什用类似的方法测试万有引力。这项工作使卡文迪什后来成了第一位直接测定引力常数的实验者。正是由于米切尔的鼓励，卡文迪什做了同心球的实验。

但是卡文迪什的同心球实验结果和他自己的许多看法，却没有公开发表。直到 19 世纪中叶，开尔文（即 W.汤姆孙）发现卡文迪什的手稿中有圆盘和同半径的圆球所带电荷的正确比值，才注意到这些手稿的价值，经他催促，才于 1879 年由麦克斯韦整理发表。卡文迪什的许多重要发现竟埋藏了一百年之久。对此，麦克斯韦写道：

“这些关于数学和电学实验的手稿近 20 捆，”其中“物体上电荷（分布）的实验，卡文迪什早就写好了详细的叙述，并且费了很大气力书写得十分工整（就像要拿出去发表的样子），而且所有这些工作在 1774 年以前就已完成，但卡文迪什（并不急于发表）仍是兢兢业业地继续做电学实验，直到 1810 年去世时，手稿仍在他自己身边。”[10]

卡文迪什出身于贵族家庭，家产厚禄，他都没有兴趣，一心倾注在科学研究之中，早年攻化学和热学，发现氢氧化合成水。他后来做的电学实验有：电阻测量，比欧姆早几十年得到欧姆定律；研究电容的性质和介质的介电常数，引出了电位的概念；他发现金属的温度越高，导电能力越弱，等等。他的同心球实验比库仑用扭秤测电力的实验早 11 年，而且结果比库仑精确。对于卡文迪什把全副心身倾注在科学研究工作上的这种精神，麦克斯韦继续写道：

“卡文迪什对研究的关心远甚于对发表著作的关心。他宁愿挑起最繁重的研究工作，克服那些除他自己没有别人会重视甚至也没有别人知道的那些困难。我们毋庸怀疑，他所期望的结果一旦获得成功，他会得到多么大的满足，但他并不因此而急于把自己的发现告诉别人，不像一般搞科研的人那样，总是要保证自己的成果得到发表。卡文迪什把自己的研究成果捂得如此严实，以至于电学的历史失去了本来面目。”

卡文迪什性情孤僻，很少与人交往，惟独与米切尔来往密切，米切尔当过卡文迪什的老师，他们共同讨论，互相勉励。为了“称衡”星体的重量，米切尔曾从事大量天文观测。他们的共同理想是要把牛顿的引力思想从天体扩展到地球，进而扩展到磁力和电力。米切尔发现了磁力的平方反比定律，但他没能完成测量电力和地球密度的目标。卡文迪什正是为了实现米切尔和他自己的愿望而从事研究。可以说，米切尔和卡文迪什是在牛顿的自然哲学的鼓舞下坚持工作的。他们证实了磁力和电力这些长程力跟引力具有同一类型的规律后，并不认为达到了最终目标，还力图探求牛顿提出的短程力。卡文迪什在他未发表的手稿中多处涉及动力学、热学和气体动力学，都是围绕着这个中心，只是没有明确地表达出来。米切尔则把自己对短程力的普遍想法向普利斯特利透露过，在普利斯特利的著作——1772 年发表的《光学史》一书中记述了米切尔的思想[11]。

3.3.3 库仑的电扭秤实验

人们公认库仑定律是库仑在 1785 年发现的，这一年，他发表了第一篇有关电荷作用力的论文，报导他对电力随距离变化的研究。他用的实验装置是他发明的电扭秤，如图 3 – 17。这是一个直径和高均为 12 英寸（30 厘米）的玻璃缸，上面盖一块玻璃板，盖板上开了两个洞。中间的洞装有一支高 24 英寸（60 厘米）的玻璃管。管的顶端有一螺旋测角器，下连银丝，银丝下端挂一横杆，杆的一端为一小球 a，另一端贴一纸片 g 作配平用。圆缸顶上刻有 360 个分格，可以读数。银丝自由垂放时，横杆上的小木球指零刻度。他先使固定在绝缘竖杆末端的另一个大小相同的小球 b 带电，然后使之与小球 a 接触后分开，这样可使电荷在两球间均分，即带等量同号电荷而互相排斥。然后借银扭丝恢复两球的原始位置，从扭丝的转角可以测知电力的大小。库仑在论文中举了一组数据，两小球相距 36 个刻度、18 个刻度和 8.5 个刻度，即间距大体上是，得到银丝分别扭转了 36 个刻度、144 个刻度和 576 个刻度。即电力约为 1∶2²∶4²。于是，库仑得出了“带同号电的两球之间的斥力，与两球中心之间距离的平方成反比”的结论。

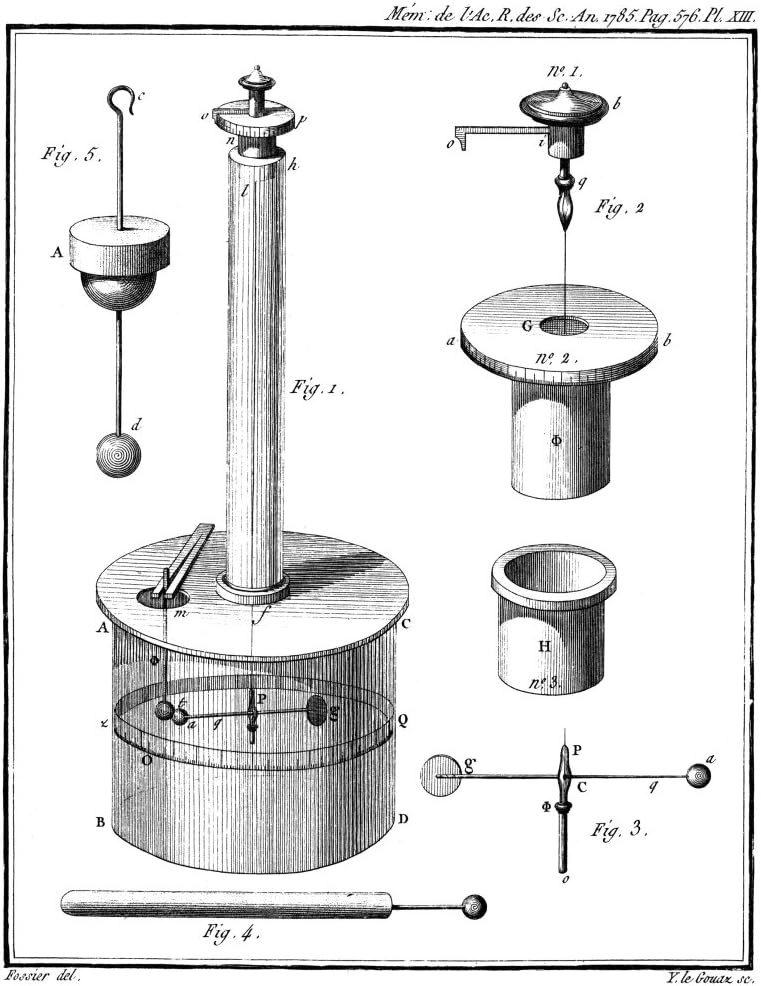
1787 年库仑宣读了第二篇论文，在论文中，库仑说明了电扭秤方法的欠缺，它用于测量异号电荷的吸引力时遇到了困难。因为活动小木球的平衡是一种不稳定的平衡，即使能达到平衡，最后“两球也往往会相碰，这是因为扭秤十分灵活，多少会出现左右摇摆的缘故。”尽管如此，库仑声称他还是得到了电吸引力也满足平方反比规律的结果。

库仑在这篇文章还报导了第二种测量方法——电摆实验。其原理与万有引力作用下的单摆实验相似。地面上单摆周期为

\[T = 2\pi \sqrt {\frac{L}{{Gm}}}  \cdot r\]

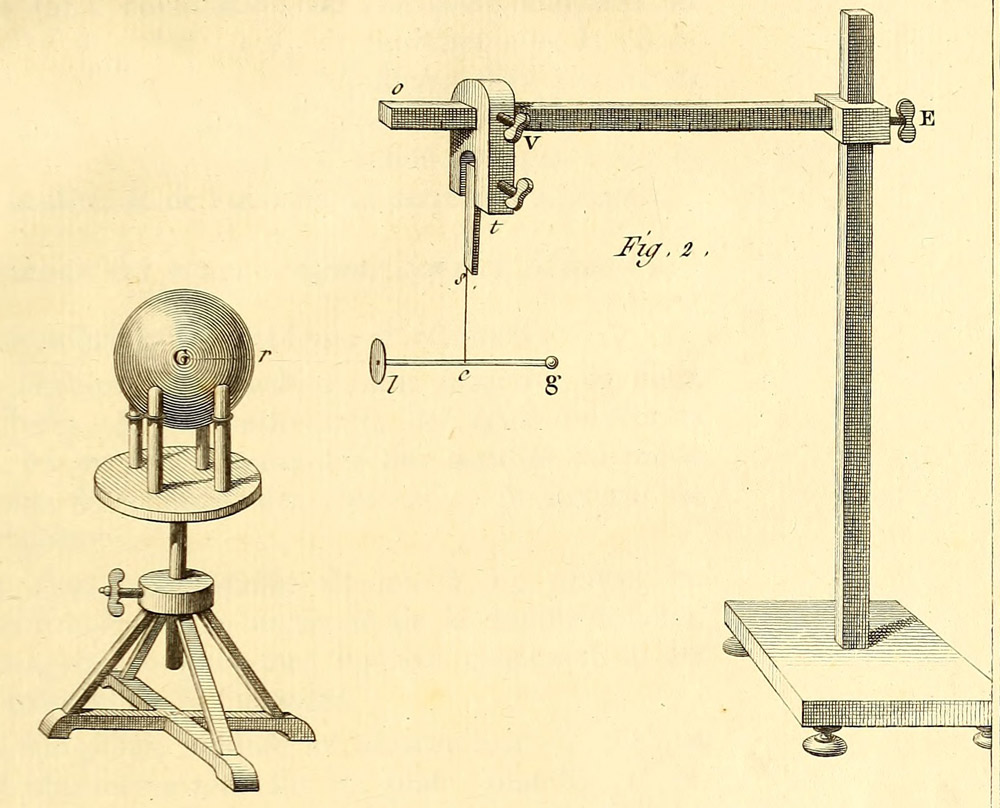
其中 G 为万有引力常数，m 和 r 为地球的质量和半径，L 为摆线长度。如果电引力也遵从平方反比规律，则图 3 – 18 中电摆 lg 的振动周期也应与其带电端 l 和另一固定的带异号电荷的金属球 G 之间的距离成正比。库仑在论文中列举了三次测量的结果，l，g 间距比取为 3∶6∶8，测得电摆周期比为 20∶41∶60，相当于 3∶6.15∶9，两者接近于正比关系。库仑认为误差是由于实验过程中的漏电，致使电引力逐渐变小，周期相应变大。经过修正，实验值与理论值才基本相符。于是他得出结论：“正电与负电的相互吸引力，也与距离的平方成反比”。从这两篇论文可以看出，库仑作出电力随距离变化的平方反比定律的发现，关键的实验不是电扭秤实验，而是电摆实验定律。因为同号电荷的斥力早已有普利斯特利的论断，而异号电荷的吸引力则是第一次出现在文献中。

在同一篇论文里，库仑还分别通过扭秤法和摆动法来测定磁力，也得出了同距离平方成反比的规律。

从库仑的发现经过可以看出，平方反比的关系自始至终对他的实验起着指导作用，例如：

（1）库仑虽然直接测量了电荷之间作用力与距离的关系，但精确度毕竟有限，如果用平方反比关系表示，其指数偏差 δ 可达0.04。如果库仑不是先有平方反比的概念，他为什么不用 F ∝ \(\frac{1}{{{r^{2.04}}}}\) 或 F ∝ \(\frac{1}{{{r^{1.96}}}}\) 来表示呢？

（2）库仑并没有改变电量进行测量，而是说“假说的前一部分无需证明”，显然他是在模仿万有引力定律，认为电力分别与相互作用的两个电荷量成正比，就如同万有引力分别与相互作用的两个物体的质量成正比一样。

（3）库仑在另一篇论文中还提到磁力的平方反比关系，库仑的实验当然是认真的，他如实地发表了实验结果。不过，他在行文中用了如下词汇：“非常接近 16∶4∶1，可见，磁力和距离的平方成反比”。他还写道：“看来，磁流体即使不在本质上，至少也在性质上与电流体相似。基于这种相似性，可以假定这两种流体遵从若干相同的定律。”

（4）库仑和上面提到的几位先行者一样，都是按万有引力的模式来探讨电力的规律性。他曾写道：“我们必须归结于那些人们为了解释物体重量和天体物理现象时不得不采用的吸引力和排斥力性质。”[12]

从库仑定律的发现经过，我们可以看到类比方法在科学研究中所起的作用。如果不是先有万有引力定律的发现，单靠实验的探索和数据的积累，不知要到何年才能得到严格的库仑定律的表达式。

实际上，整个静电学的发展，都是在借鉴和利用引力理论的已有成果的基础上取得的。在库仑之后，科学家沿着牛顿引力理论开辟的道路继续走下去。分析力学经过欧拉、拉格朗日和拉普拉斯等人的工作，建立了势函数的概念，势函数 V 满足下述拉普拉斯方程

\[\frac{{{\partial ^2}V}}{{\partial {x^2}}} + \frac{{{\partial ^2}V}}{{\partial {g^2}}} + \frac{{{\partial ^2}V}}{{\partial {z^2}}} = 0\]

我们现在知道，这是引力场的基本特征（有势场）。

1813 年，泊松（Simeon D.Poisson，1781—1840）用数学方法严格证明了处于静电平衡的导体内部的任何带电粒子所受的力为零，否则导体内部就会有电荷的流动。他根据万有引力定律和库仑定律都遵从平方反比关系，认为静电学同样可以找出与万有引力情况相似的函数 V 来求解静电学问题，并把拉普拉斯方程推广为泊松方程

\[\frac{{{\partial ^2}V}}{{\partial {x^2}}} + \frac{{{\partial ^2}V}}{{\partial {g^2}}} + \frac{{{\partial ^2}V}}{{\partial {z^2}}} = 4\pi \rho \]

其中 ρ 为电荷密度。

1828 年格林（George Green，1793—1841）进一步提出了格林定理。1839 年，高斯在他的著作《与距离平方成反比的吸引力和推斥力的普遍理论》中阐明势理论的原理，其中包括静电学的基本定理——高斯定理

\[\oint {E \cdot dS = \frac{1}{{{\varepsilon _0}}}\Sigma q} \]

高斯还为电量确定了单位，他提出应该由库仑定律本身来定义电荷的量度，即两个距离为单位长度的相等电荷间的作用力等于单位力时，这些电荷的电量就定义为单位电荷。有了电量这一物理量，才有可能完整地按照万有引力定律的形式表达电力的平方反比定律

\[f = k\frac{{{q_1}{q_2}}}{{{r^2}}}\]

诚然，电学的发展得益于牛顿力学的启示，得益于类比方法，然而，实验验证的作用无论如何也是不能抹煞的。试想，如果没有库仑等人的精确（在当时的时代局限下，应该说已经达到了很高的精确度）测量，谁能对这一未知领域的新现象作出科学的决断呢？然而，我们下面将会看到，类比方法也有它的局限性，在电磁学的历史中就有许多教训。

[1] 自然现象中许多过程都服从平方反比关系，例如：光的照度、水向四面八方喷洒、均匀固体中热的传导等无不以平方反比变化，这从几何关系就可以得到证明。因为同一光通量、水量、热量等，通过同样的球面，球面的面积 S 与关径 r 的平方成正比，即 S = 4πr²，所以强度与半径的平方成反比。如果在传播过程中有干扰的媒质，例如有一透镜置于光路中，就会使光的分布发生畸变，这就出现各向异性。所以，平方反比定律假定的基础是空间的均匀性和各向同性。

[2] Goodman.The Ingenius Dr.Franklin.Oxford，1931.144

[3] 转引自：Turner D M，Makers of Science：Electricity and Magnetism.Oxford，1927.28

[4] 即以 IH 和 KL 为界的粒子的质量，应与弧长的平方成正比，而弧长又与距离成正比。

[5] Newton.I.，Mathematical Principles of Natural Philosophy.California，1946.193

[6] Heilbron J L.Electricity in the 17^th & 18^th Centuries.University of California Press，1979.468

[7] 转引自：Turner D M.Makers of Science；Electricity and Magnetism.Oxford，1927.34

[8] 牛顿著，王克迪译.自然哲学之数学原理·宇宙体系，武汉出版社，1992.420

[9] 转引自：Wolf A.A History of Science，Technology and Philosophy in the Eighteenth Century.MacMillian，1939.270

[10] Maxwell J C.The Electrical Researches of the Honourable Henry Cavendish.Cambridge，1879.45

[11] McCormmach R.British Journal of History of Sciences，1968（4）：126

[12] 转引自：钱临照，许良英主编.世界著名科学家传记·物理学家 Ⅱ，科学出版社，1992.49

发布时间：2010/9/16 下午3:45:57  阅读次数：15680