第五章 第四节 向心力 向心加速度

图 5–32 链球运动
链球是田径运动中的一种投掷项目。球体用铁或铜制成,装有链子和把手。运动员两手握着把手,人和球同时旋转,经加速旋转后,运动员猛然松手使链球飞出。
本节编写思路
本节中创设情境时,可以先介绍链球运动的世界纪录、中国女子链球运动员在奥运赛场上的战绩等,然后再介绍链球投掷的过程,很自然地引入向心力的概念。
本节内容主要研究做匀速圆周运动物体的受力特点,教学中要引导学生将牛顿运动定律用于研究匀速圆周运动,进一步体会力是改变物体运动状态的原因,丰富知识的结构,深化运动与相互作用的观念。向心力概念的建立和理解是本节的重点和难点。教材第一部分内容围绕向心力概念的建立,从对赛场上链球运动的分析到自主活动中的操作、感受,逐步形成对向心力的认识;第二部分内容在定性实验的基础上,通过定量实验探究向心力公式;第三部分内容根据牛顿第二定律通过理论演绎建立向心加速度概念,并得出向心加速度公式。
在链球比赛中,为了使链球飞得更远,运动员会拉着链条的一端旋转,使系在链条另一端的链球跟着做圆周运动,如图 5–32 所示。经过 3 ~ 4 圈加速旋转,运动员猛然松手使链球飞出。

图 5–33 转圈的小球
如图 5–33 所示,在细绳的一端系一个小球,用手捏住绳子另一端,使小球在水平放置的玻璃平板上绕被捏住的绳子一端转圈。
细绳对小球拉力的方向与小球的速度方向有什么关系?将手松开,观察小球是否能继续转圈。
此处设置“自主活动”是为了让学生体验向心力的存在:先让学生感受小球做圆周运动时手上受到的力,然后观察现象——松手后小球就不再做圆周运动,帮助学生认识到做圆周运动的物体必须受到指向圆心的力。
上述活动中,当手松开后,小球不再受拉力作用,脱离圆周,沿切线方向飞出。
研究表明,物体做匀速圆周运动的条件是受到与物体的速度方向垂直、指向圆心且大小不变的合力作用,这个力叫做向心力(centripetal force)。
示例 1 游乐场里有一种旋转飞椅,当飞椅以一定的速率旋转时,游客和飞椅一起在水平面内做匀速圆周运动,如图 5–34 所示。将飞椅和游客视为整体,分析其受到的向心力的来源。
示例 1 的教学目的在于:① 认识向心力是物体做圆周运动的必要条件;② 体会向心力可以由一个或几个施力物体提供;③ 理解向心力是一个以效果命名的力,它可以是我们熟悉的弹力、摩擦力、重力中的任何一种力,也可以是它们的合力或分力;④ 理解向心力始终指向圆心,它只改变速度方向,不改变速度大小。

图 5–34 旋转飞椅
图 5–35 游客的受力示意图
分析:以某一游客和所坐的飞椅为研究对象,将其视为质点,其受力情况可抽象成如图 5–35 所示的示意图。根据质点做匀速圆周运动的轨迹,可确定运动所在圆周的圆心,进而可确定质点所受向心力的方向。对质点进行受力分析,所受力的合力就是质点做匀速圆周运动的向心力。
解:如图 5–35 所示,以飞椅和游客整体为研究对象,其在水平面内做匀速圆周运动,受到的向心力一定指向轨迹的圆心 O。根据受力分析,飞椅和游客整体受到重力 G 和沿吊绳向上的弹力 FT 的作用,两个力的合力 F 就是其所受的向心力,该合力一定在水平面内,并且指向 O 点。
向心力是根据作用效果命名的力,重力、弹力、摩擦力或者这些力的合力都可以作为向心力。
在前面的自主活动中,改变小球运动的快慢、细绳的长度与小球的质量,感受手上拉力大小的变化,猜测向心力的大小可能与哪些因素有关。
通过“大家谈”让学生猜测影响向心力大小的可能因素,引出定量实验研究的方向。
我们猜想:向心为的大小可能与做匀速圆周运动物体的圆周半径、运动快慢和质量都有关,它们有什么定量关系呢?这需要通过定量的实验来研究。
该实验是一个学生实验,建议先引导学生猜想,然后采用控制变量的方法,逐个得出向心力与物体质量、角速度、圆周半径的关系。
探究向心力大小与半径、角速度、质量的关系
本实验涉及的物理量较多,数据测量较为复杂,教材中已给出明确的实验装置和测量步骤。
实验装置及操作说明:
(1)为了便于测量运动中物体受到的力和运动速度的大小,本实验使用无线力传感器和无线光电门传感器,它们测得的数据通过无线接收器传送至计算机。
(2)实验中,光电门传感器测得的是每次悬臂顶端经过挡光装置时的线速度,该速度与悬臂半径的比就是砝码的角速度,角速度乘以砝码运动的半径可得到砝码运动的线速度。相比较而言,砝码运动的角速度比其线速度容易测量,而且更容易控制,因此本装置适宜研究向心力的大小与物体运动的半径、角速度、质量的关系。
(3)实验中,砝码固定在水平连杆上,所需向心力由连杆提供。为了消除连杆本身对实验的影响,在悬臂的另一侧也安装有一根同样的水平连杆。
提出问题
物体做匀速圆周运动时所受向心力的大小与物体运动的圆周半径、运动快慢及质量有关,向心力大小与这些因素之间有何定量关系?
实验原理与方案
向心力大小 F 与半径 r、角速度 ω、质量 m 都有关,本实验需要采用控制变量法。分别研究:(1)ω 与 m 一定时,F 与 r 的关系;(2)r 与 m 一定时,F 与 ω 的关系;(3)r 与 ω 一定时,F 与 m 的关系。
综合三个实验研究的结论,探究向心力大小 F 与半径 r、角速度 ω、质量 m 的关系。
实验装置与方法
图 5–36 所示的实验装置可供本实验选用。在电动机控制下,悬臂可绕轴在水平面内匀速转动,在悬臂的转轴上固定一个无线力传感器;水平连杆的一端与无线力传感器相连,连杆上可固定砝码;无线光电门传感器安装在悬臂的一端,挡光片固定在支架上。当悬臂匀速转动时,砝码随之做匀速圆周运动。实验中力传感器测出对连杆的拉力大小等于砝码受到的向心力大小;砝码的运动半径可由悬臂上的刻度读出;测出光电门通过挡光片的瞬时速度,进而可得到悬臂旋转的角速度,即砝码的角速度。
本实验采用作图的方法分析数据,研究物理量间的函数关系。
图 5–36 研究向心力的实验装置
①悬臂
②无线力传感器
③砝码
④水平连杆
⑤无线光电门传感器
⑥挡光片
⑦电动机控制器
⑧电动机
实验操作与数据收集
根据实验原理与方案的要求,使悬臂带动砝码做匀速圆周运动,测量并记录相关实验数据,填入表 5–3、表 5–4 和表 5–5。
表 5–3 实验数据记录表(ω、m 一定)
|
实验序号 |
1 |
2 |
3 |
4 |
5 |
|---|---|---|---|---|---|
|
r/m |
|
|
|
|
|
|
F/N |
|
|
|
|
|
表 5–4 实验数据记录表(r、m 一定)
|
实验序号 |
1 |
2 |
3 |
4 |
5 |
|---|---|---|---|---|---|
|
ω/(rad·s−1) |
|
|
|
|
|
|
F/N |
|
|
|
|
|
表 5–5 实验数据记录表(ω、r 一定)
|
实验序号 |
1 |
2 |
3 |
4 |
5 |
|---|---|---|---|---|---|
|
m/kg |
|
|
|
|
|
|
F/N |
|
|
|
|
|
数据分析
根据实验数据,选择合适的坐标系描点作图,研究相关物理量间的关系。
实验结论
做匀速圆周运动的物体,当:
(1)ω 与 m 一定时,___________________________________________________;
(2)r 与 m 一定时,___________________________________________________;
(3)ω 与 r 一定时,___________________________________________________。
向心力 F 与 r 、ω 、m 的关系是:__________________________________________。
交流与讨论
(1)各组就实验数据进行交流,比较、分析实验结果的异同及其原因,探讨实验的改进方法。
本实验的重点在于培养学生参照实验方法实施操作、记录数据、处理分析数据、发现特点、形成结论等诸方面的实验素养,引导学生学会用物理术语、图表等交流探究的过程和结果等。
(2)线速度、角速度都可以描述物体做匀速圆周运动的快慢,用本实验装置能否直接研究向心力大小与半径、线速度、质量的关系?
大量的研究表明,做匀速圆周运动物体受到的向心力 F 的大小等于物体的质量 m、圆周半径 r 和角速度 ω 的二次方的乘积,即
\[\color{#357A4A}{F = m{\omega ^2}r}\]
将 v = ωr 代入上式,即可得
\[\color{#357A4A}{F = m\frac{{{v^2}}}{r}}\]
物体做匀速圆周运动时受到的合力始终指向圆心,根据牛顿第二定律,它的加速度也始终指向圆心,与线速度的方向垂直,如图 5–37 所示。因此,匀速圆周运动的加速度叫做向心加速度(centripetal acceleration),向心加速度只改变速度的方向,不改变速度的大小。
通过实验得出向心力公式后,可由牛顿第二定律方便地得出向心加速度公式,培养学生的推演能力。
教师可根据学生的情况,给学生介绍“向心加速度公式的理论推导”(见节后资料链接),提高学生演绎推理的能力。
向心加速度 a 和线速度 v、角速度 ω 的矢量关系式为
a = ω×v
由向心力公式和牛顿第二定律可以得出向心加速度的表达式为
\(\color{#357A4A}{a = {\omega ^2}r}\) 或 \(\color{#357A4A}{a = \frac{{{v^2}}}{r}}\)
在匀速圆周运动中,由于 r、v 和 ω 的大小是不变的,所以向心加速度的大小不变,但向心加速度的方向始终指向圆心,一直在变化,因此,匀速圆周运动是变加速运动。
图 5–38 物体随转盘匀速转动
示例 2 如图 5–38 所示,质量 m = 3 kg 的物体放在水平的转盘上,在半径 r = 2 m 的圆周上以 v = 4 m/s 的速度随转盘做匀速圆周运动。求:
(1)物体的向心加速度大小;
(2)物体受到的静摩擦力。
分析:由匀速圆周运动的线速度和半径,可直接求出向心加速度。对物体进行受力分析,根据运动状态可确定物体受到的重力和支持力在竖直方向平衡,平台对物体的静摩擦力提供物体做匀速圆周运动所需的向心力。根据牛顿第二定律可求出物体受到的向心力,即静摩擦力。
解:(1)由于物体随转盘一起做匀速圆周运动,其向心加速度的大小
\[a = \frac{{{v^2}}}{r} = \frac{{{4^2}}}{2}\;{\rm{m/}}{{\rm{s}}^{\rm{2}}} = 8\;{\rm{m/}}{{\rm{s}}^{\rm{2}}}\]
图 5–39 物体的受力分析
(2)如图 5–39 所示,物体受到三个力的作用,其中重力 G 和支持力 FN 平衡,转盘对物体的静摩擦力 Ff 指向圆心,作为物体受到的向心力。
因此,由牛顿第二运动定律,物体受到的静摩擦力
\[{F_f} = ma = 3 \times 8\;{\rm{N}} = 24\;{\rm{N}}\]
静摩擦力的方向始终指向圆心。
图 5–40 曲线运动中合力的分解
一般情况下,做曲线运动的物体,其速度的大小和方向都在改变,它受到的合力可以沿切线方向和法线方向分解,如图 5–40 所示。切线方向的力改变速度的大小,法线方向的力改变速度的方向。
此处设置“拓展视野”是为了帮助学生将对向心力的认识推广到一般曲线运动,知道圆周运动中的向心力就是法向力。教师可根据学生的认知程度和课时情况选用。
- 试根据力、质量、速度和半径的单位,判断向心力公式 F = m\(\frac{{{v^2}}}{r}\) 是否合理。
- 关于向心加速度与半径的关系,甲同学认为,根据公式 a = ω2r 得 a 与 r 成正比;乙同学认为,根据公式 a = \(\frac{{{v^2}}}{r}\) 可得 a 与 r 成反比。试对这两种截然不同的说法做出评价。
- 由于地球的自转,地球上的物体都有向心加速度,试回答:
(1)“在地球表面各处的向心加速度的方向都是指向地心的”,这种说法是否正确?为什么?
(2)在赤道和极地附近的向心加速度哪个大?为什么?
(3)在上海的物体由于地球自转而产生的向心加速度为多大?
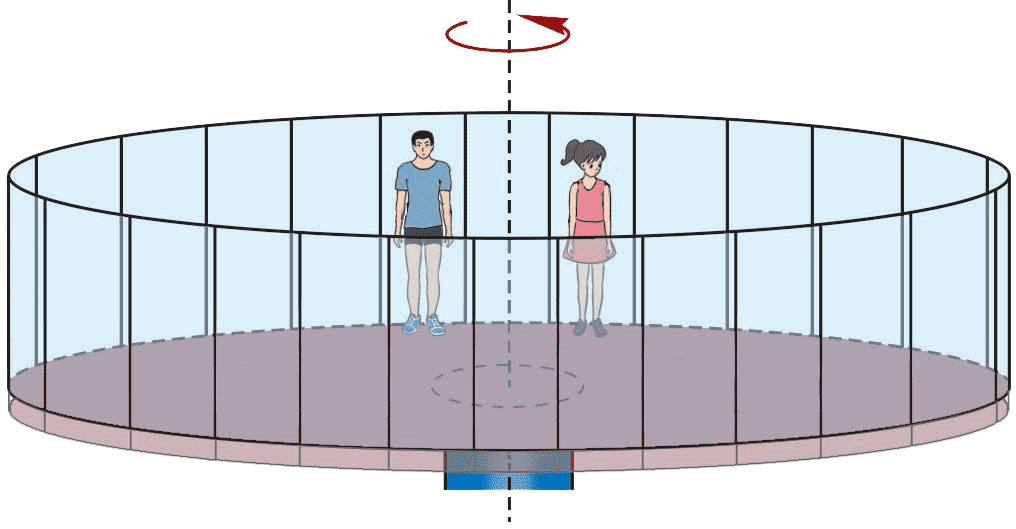
图 5–41
- 有一种游乐项目,游客进入一个大型圆筒状容器后,紧靠竖直筒壁站立(图 5–41)。当圆筒开始转动后,转速逐渐增大,游客会感到自己被紧紧地压在筒壁上;当转速增大到一定数值时,底板突然下落了几厘米,游客们惊奇地发现自己己竟然没有跟着底板一起下落!解释这一现象?
- 若旋转餐厅转动一周的时间约为 1 h,某顾客坐在离转轴距离约为 20 m 的座位上。计算该顾客受到的向心力与重力的比值。
- 线的一端系一个重物,手执线的另一端使重物在光滑水平桌面上做匀速圆周运动。在使重物运动周期相同的条件下,使用长线易断还是短线易断?为什么?
图 5–42
- 在如图 5–42 所示的装置中,A、B 两个小球穿在光滑杆上并可沿杆滑动,两球之间用一根细线连接。甲、乙两位同学就“装置绕轴匀速转动时,如何能使两球相对光滑杆静止”这一问题展开讨论。甲认为,两个小球放置在任意位置都可以。乙则认为,两个小球只有放置在特定位置才可以。你赞同哪个观点?试为这个观点作进一步论证。
问题与思考解读
1.参考解答:合理,因为 1 \(\frac{{{\rm{kg \times (m/s}}{{\rm{)}}^{\rm{2}}}}}{{\rm{m}}}\) = 1 kg·m/s2 = 1 N
命题意图:从物理量单位推演的角度理解物埋公式和物理量间的关系。
主要素养与水平:科学推理(Ⅱ)。
2.参考解答:这两种结论都正确,但前提不同,在角速度相同的情况下,a 与 r 成正比;在线速度相同的情况下,a 与 r 成反比。
命题意图:对两种截然不同的结论进行评价,引导学生全面考虑问题,形成在应用物理规律时要注重规律前提的意识,养成全面思考问题的科学态度。
主要素养与水平:质疑创新(Ⅰ)。
3.参考解答:(1)不正确。处于地表不同纬度的物体做圆周运动的圆心位于地轴上的不同位置,随地球自转的物体的向心加速度方向在所在纬度平面内指向地轴。
(2)在赤道处物体的向心加速度比较大。因为不同位置物体的角速度相同,根据 a = ω2r,赤道处物体的运动半径大,所以向心加速度也大。
(3)上海位于北纬 30°附近,r = R地cos30°,地球自转周期为 24 h,根据 ω = \(\frac{{2\pi }}{T}\) 和 a = ω2r,可求得 a ≈ 0.03 m/s2。
命题意图:以物体随地球自转为情境,抽象出物理模型,加深对加速度的理解。
主要素养与水平:运动与相互作用(Ⅱ);模型建构(Ⅱ);科学推理(Ⅱ);科学论证(Ⅱ)。
4.参考解答:人受到竖直向下的重力、指向圆心的弹力和竖直向上的摩擦力,向心力由这三个力的合力提供;或者说摩擦力和重力相互平衡,筒壁给人的弹力提供向心力。当转速足够大时,向心力的大小,即筒壁的弹力足够大,导致人和筒壁间的最大静摩擦力大于人受到的重力,人就不会往下掉。
命题意图:综合应用静摩擦力、向心力的知识,解决生活中的实际问题,提高解决综合问题的能力。
主要素养与水平:运动与相互作用(Ⅱ);科学推理(Ⅱ);科学论证(Ⅱ)。
5.参考解答:设顾客的质量为 50 kg。根据已知条件,他随餐厅做圆周运动的周期 T = 1 h = 3 600 s,运动半径 r = 20 m。由公式 F = mω2r 和 ω = \(\frac{{2\pi }}{T}\) 可得 F = m\(\frac{{4{\pi ^2}}}{{{T^2}}}\)r。代入数据可得 F ≈ 3.05×10−3 N。向心力与重力的比值 \(\frac{F}{G}\) ≈ 6.22×10−6,可见这个比值非常小,所以顾客感觉不到。
命题意图:通过建模、估算,巩固向心力知识,讨论生活中的实际问题。
主要素养与水平:运动与相互作用(Ⅱ);科学推理(Ⅱ)。
6.参考解答:长线易断。由向心力公式 F = mω2r 和 ω = \(\frac{{2\pi }}{T}\) 可得 F = m\(\frac{{4{\pi ^2}}}{{{T^2}}}\)r。当周期相同时,线越长即重物做圆周运动的半径越大,所需向心力越大,线越容易断。
命题意图:针对问题情境,选择适合的向心力公式解决问题。
主要素养与水平:科学论证(Ⅱ)。
7.参考解答:乙的观点正确。两个小球只有放置在特定位置才可以相对杆静止。两球所受向心力均来自细线的拉力,大小相等;两球的角速度相等,根据公式 F = mω2r 可以得出两球做圆周运动的半径与两球的质量成反比,所以位置由两球的质量之比决定。
命题意图:在真实情境中抽象出物理模型,综合运用圆周运动相关知识,经过分析、推理解决问题。
主要素养与水平:科学推理(Ⅱ);科学论证(Ⅲ)。
参考资料
向心加速度公式的理论推导
我们可以根据向心加速度的定义确定其方向,并从理论上推导其表达式。
如图 8(a)所示,质点沿半径为 r 的圆周做匀速圆周运动,质点在 A 点时的速度为 vA,经过很短的时间 Δt 运动到 B 点,速度变为 vB,圆弧 AB 的圆心角为 Δφ。如图 8(b)所示,根据矢量和的三角形法则,图中 Δv 是质点从 A 运动到 B 过程中速度的变化量。比值 \(\frac{{\Delta v}}{{\Delta t}}\) 就是质点在 Δt 时间内的平均加速度,方向跟 Δv 的方向相同。当 Δt 趋近于 0 时,Δφ 也趋近于 0,这时 Δv 便趋近于与 vA 垂直,而 vA 的方向在圆周的切线上,所以 Δv 的方向趋近于沿半径指向圆心。因此,质点做匀速圆周运动时在任一点的加速度都是沿着半径指向圆心的,这也是向心加速度一词的由来。
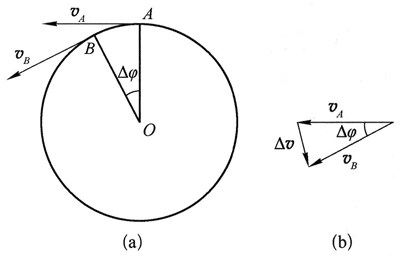
从图 8 可以看出,图(b)中的矢量三角形跟图(a)中的 △OAB是相似的。因为 vA = vB,可用 v 表示 vA、vB 的大小,则有
\[\frac{{\left| {\Delta v} \right|}}{v} = \frac{{AB}}{r}\]
即 | Δv | = AB·\(\frac{v}{r}\)
将上式两边同时除以 Δt,有
\[\frac{{\left| {\Delta v} \right|}}{{\Delta t}} = \frac{{AB}}{{\Delta t}} \cdot \frac{v}{r}\]
当 Δt → 0 时,A、B 间弦长趋近于 A、B 间圆弧长,等式左边 \(\frac{{\left| {\Delta v} \right|}}{{\Delta t}}\) 即为向心加速度 a 的大小,右边的 \(\frac{{AB}}{{\Delta t}}\) 就是匀速圆周运动的线速度大小 v,代入整理得
\[a = \frac{{{v^2}}}{r}\]
这就是匀速圆周运动的向心加速度公式。
发布时间:2022/2/3 上午11:04:14 阅读次数:10725
