第 3 节  向心加速度  教学建议

1．教学目标

（1）知道匀速圆周运动中向心加速度大小的表达式，理解向心加速度与半径的关系，并会用来进行简单的计算。

（2）了解分析匀速圆周运动速度变化量时用到的极限思想。

（3）能根据问题情景选择合适的向心加速度的表达式。

2．教材分析与教学建议

向心加速度是描述匀速圆周运动的又一重要概念，教材在“问题”栏目中，从运动和力的关系出发，确定做圆周运动的物体具有加速度。本节是前一节“向心力”的拓展，同时又是学好后一节“生活中的圆周运动”的前提，具有承上启下的作用。

本节的重点是向心加速度的方向和大小。教材从动力学角度出发，根据“从力推知加速度”的思路，在前一节确定的向心力方向和大小的基础上，得出向心加速度的方向和大小。这种叙述的好处是降低了教学的难度，使学生可以较容易地掌握向心加速度的概念。

教材在“拓展学习”栏目中根据加速度定义式推导向心加速度的方向和大小，在推理过程中渗透极限思想。这是为学有余力的学生开的“窗口”，并不是所有学生需要达到的要求。这种编写思路不仅体现了学习的层次性，也让学生经历多角度认识问题的思维过程，体验多角度分析问题的方法，有利于提升学生科学思维的素养。

（1）匀速圆周运动的加速度方向

从动力学的角度得到向心加速度的方向难度并不大。从培养学生科学思维的角度，还可以引导他们从运动学角度分析向心加速度的方向。教材中这部分内容放在“拓展学习”栏目中，对于学有余力的学生，也可以在课堂上进行。

在从运动学角度学习向心加速度的概念时，学生可能会遇到来自三个方面的困难。①已有经验的阻碍作用。受直线运动中加速度概念的影响，学生会认为匀速圆周运动速度大小没有改变，没有加速度。②相关知识经验的不足。学生知道速度是矢量，但对不共线矢量减法运算的知识储备不足，对确定速度变化量的方向感到困难。③不理解近似、极限思想。对小角度时采用的近似、极限处理有很大困难。这就需要教师精心设计问题，并让学生进行充分的讨论。

教学片段

探究匀速圆周运动加速度的方向

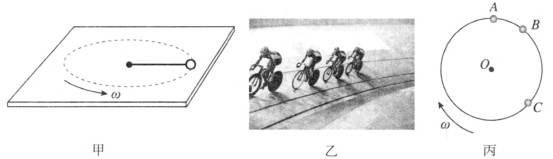
问题 1．图 6–12 甲中的小球与图 6–12 乙中的运动员正在做匀速圆周运动，是否具有加速度？

问题 2．做匀速圆周运动的物体的加速度方向如何确定？你的依据是什么？

问题 3．除了用牛顿第二定律确定向心加速度的方向外，你还有什么方法可确定向心加速度的方向？

（2）匀速圆周运动的加速度大小

教学片段

探究匀速圆周运动的加速度大小

问题 1．图 6–12 甲中的小球正以角速度 ω 做半径为 r 的匀速圆周运动，它的向心加速度大小是多少？

问题 2．计算向心加速度的公式除了 a = ω²r 外，还有其他表达式吗？

问题 3．根据 a = ω²r 与 a = \(\frac{{{v^2}}}{r}\)，请分析向心加速度与半径究竟是成正比，还是成反比？该如何理解这一问题？

问题 4．物体做变速圆周运动时，向心加速度的表达式 a = ω²r 与 a = \(\frac{{{v^2}}}{r}\) 是否成立？为什么？

问题 5．我们可以从牛顿第二定律推导出向心加速度大小的表达式，是否还有其他方法？

---

从牛顿第二定律角度推导向心加速度的表达式是比较容易的。对于基础较好的学生，可以通过问题 5 启发他们，尝试自己推导。

教学片段

运用向心加速度的公式解决实际问题

问题 1．如图 6–13 甲所示，A、B、C 分别是大齿轮、小齿轮边缘上的点和后轮边缘上的点，当转动脚踏板时，这三点间的加速度大小如何比较？你选择公式的依据是什么？

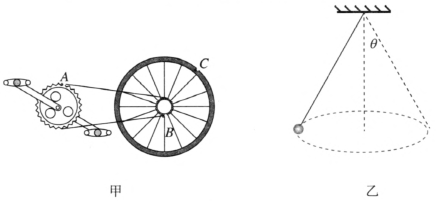
问题 2．如图 6–13 乙所示，长为 l 的绳子拴有质量为 m 的小球，在同一水平面内做匀速圆周运动，绳与竖直线的夹角为 θ。小球的加速度方向指向哪里？

问题 3．小球受几个力的作用，是什么力提供了向心力？

问题 4．生活经验告诉我们，如果转动得快，绳与竖直线的夹角 θ 就大，你能够给出理论依据吗？

---

比较 A、B 两点的加速度时，考虑到链条的约束，两点的线速度大小相等，应选择 a = \(\frac{{{v^2}}}{r}\) 进行比较，得 a_A < a_B。比较 B、C 两点的加速度时，考虑到是同轴转动，角速度相同，应选择 a = ω²r 进行比较，得 a_B < a_C，综合可得 a_A < a_B < a_C。分析圆锥摆时，首先应进行运动和受力分析，建立圆周运动模型。明确圆周是哪个圆？圆心在哪？向心加速度方向如何？在此基础上，再明确什么力产生了向心加速度，最后再列式求解。

教学片段

从运动学视角确定向心加速度的方向

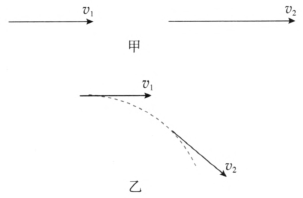
问题 1．如图 6–14 甲所示，物体做直线运动，初速度为 v₁，末速度为 v₂，如何用矢量图表示速度变化量？

问题 2．如图 6–14 乙所示，物体做曲线运动，初速度为 v₁，末速度为 v₂，如何用矢量图表示速度变化量？

问题 3．匀速圆周运动也是曲线运动，如何在图 6–15 甲中，作出质点从 A 点到 B 点速度变化量的矢量图呢？

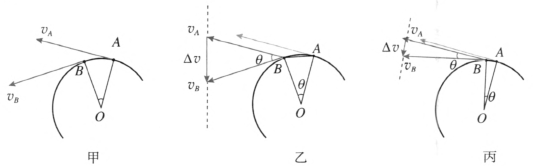
问题 4．如果 A、B 两点之间是整数个圆周，则 Δv 等于多少？如果 A、B 两点之间是半个圆周，则 Δv 等于多少，方向如何？如果 A、B 两点之间是四分之一个圆周，则 Δv 等于多少？其方向如何？

问题 5．如何确定图 6–15 乙中物体的加速度方向？

---

问题 1 主要是帮助学生回忆直线运动中如何表示速度的变化量。问题 2 以平抛运动为例，慢慢渗透矢量平移的思想。问题 3 是迁移问题 2 中所用的方法，将矢量平移运用到圆周运动中速度变化量的求法。问题 4 从几个特殊的位置看速度变化量，降低学生认识的台阶，遵循从特殊到一般的认知规律。问题 5 主要是渗透极限的思想，从运动学的角度解释为什么加速度的方向是指向圆心的。

3．“练习与应用”参考答案与提示

本节共 4 道习题，第 1 题根据向心加速度的不同表达形式，理解向心加速度以及向心加速度公式中各物理量之间的相互关系。第 2 题和第 4 题让学生在熟悉的圆周运动情境中建构模型，进行科学推理。第 3 题研究实际皮带传动模型，练习选择恰当的公式解决简单的问题。

 

1．A．乙；B．甲；C．甲；D．甲

提示：甲、乙线速度相等时，利用 a_n = \(\frac{{{v^2}}}{r}\)，半径小的向心加速度大。甲、乙周期相等时，利用 a_n = \(\frac{{4{\pi ^2}}}{{{T^2}}}\)r，半径大的向心加速度大。甲、乙角速度相等时，利用 a_n = vω，线速度大的向心加速度大。甲、乙线速度相等时，利用 a_n = vω，角速度大的向心加速度大。由于在相等时间内甲与圆心的连线扫过的角度比乙大，所以甲的角速度大，甲的向心加速度大。

 

2．2.7×10⁻³ m/s²

提示：月球公转周期 T = 27.3×24×3600 s = 2.36×10⁶ s，月球公转的向心加速度 a_n = \(\frac{{4{\pi ^2}}}{{{T^2}}}\)r = （\(\frac{{2 \times 3.14}}{{2.36 \times {{10}^6}}}\)）²×3.84×10⁸ m/s² = 2.7×10⁻³ m/s²。

以月球公转为背景，练习用 a_n = \(\frac{{4{\pi ^2}}}{{{T^2}}}\)r 求解月球的向心加速度，计算量较大，为下一章的学习埋下伏笔，培养学生对太空探索的兴趣。

 

3．（1）3∶1；（2）0.05 m/s²；（3）0.3 m/s²

提示：（1）由于皮带与两轮之间不发生滑动，所以两轮边缘上各点的线速度大小相等。

设电动机皮带轮与机器皮带轮边缘上质点的线速度大小分别为 v₁、v₂，角速度大小分别为 ω₁、ω₂，边缘上质点运动的半径分别为 r₁、r₂，则 v₁ = v₂，v₁ = ω₁r₁，v₂ = ω₂r₂，又 ω = 2πn，所以 n₁∶n₂ = ω₁∶ω₂ = r₁∶r₂ = 3∶1。

（2）A 点的向心加速度 a_nA = ω₂²×\(\frac{{{r_2}}}{2}\) = 0.10×\(\frac{1}{2}\) m/s² = 0.05 m/s²。

（3）电动机皮带轮边绦上质点的向心加速度 a_n = \(\frac{{v_1^2}}{{{r_1}}}\) = \(\frac{{v_2^2}}{{{r_2}}}\)×\(\frac{{{r_2}}}{{{r_1}}}\) = 0.1×3 m/s² = 0.3 m/s²。

皮带传动是教学中的一个难点，教学中要注意引导学生根据题设条件挖掘隐含条件，如同轴转动的角速度大小相等，同一皮带上各处的线速度大小相等。

 

4．2∶1

提示：A、B 两个快艇做匀速圆周运动，由于在相等时间内它们通过的路程之比是 4∶3，所以它们的线速度之比为 4∶3。由于它们在相等时间内运动方向改变的角度之比是 3∶2，所以它们的角速度之比为 3∶2。由于向心加速度 a_n = vω，所以它们的向心加速度之比为 2∶1。

以快艇在湖面上做匀速圆周运动为背景，练习用以 a_n = vω 求向心加速度，加深对线速度、角速度物理意义的理解。