第3章 第2节 科学探究：向心力

我们知道，物体受到的合外力方向与运动方向不在同一条直线上时，物体将做曲线运动。圆周运动是一种特殊的曲线运动，那么，做圆周运动的物体受力有什么特点呢？本节将探究物体做圆周运动时所需的向心力。

1．向心力

下面我们通过实验来探究做圆周运动物体的受力特点。

迷你实验室

向心力与圆周运动

取一根细绳，一端系一小球，另一端固定在一枚图钉上。将图钉钉于水平光滑木板上，如图3-12 所示。

（1）用手指沿小球与图钉连线的垂直方向轻轻弹击小球，在细绳未伸直前，小球做什么运动？

（2）用手指弹击小球，方向同上，加大弹击力量，使小球运动过程中细绳伸直。细绳伸直后，小球做什么运动？

上述实验中，小球在桌面上做圆周运动时，受到三个力的作用，即重力 G、桌面支持力 N 和绳子的拉力 F，合力就是绳子的拉力 F。虽然拉力的方向时刻在改变，但它始终指向圆心，这就是小球做圆周运动的原因。显然，做圆周运动的物体一定受到指向圆心的力的作用，这个力称为向心力（centripetal force）。

向心力只改变速度的方向，不改变速度的大小。如果物体做匀速圆周运动，合力提供向心力；如果物体做非匀速圆周运动（线速度大小会改变），合力的一部分提供向心力。

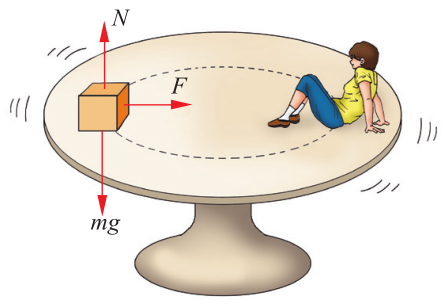
向心力可能是弹力、重力或摩擦力，也可能是某几个力的合力。例如，月球绕地球做圆周运动需要的向心力由地球对月球的引力提供；随水平圆台一起匀速转动的人或物体需要的向心力由圆台对人或物体的静摩擦力提供（图 3-13）。

物理聊吧

某乘客坐在一辆车上，当车辆转弯时，他受到的向心力来自何处？

2．探究影响向心力大小的因素

取一根空心管，将一根尼龙线穿过它，在尼龙线一端拴一块质量很小的物体，另一端挂一篮球，手握空心管抡动该物体，使该物体做圆周运动。当该物体的转速达到一定值时，篮球就会处于静止状态，甚至不断上升（图 3-14）。你能用此方法拉起更多的篮球吗？

如果依次增大被转动物体的质量、转动的半径、转动的角速度，情况会如何？

随着做圆周运动物体的质量变大、转动半径变大、角速度变大，能拉起的篮球数量也变多。由于做圆周运动的物体所需要的向心力是由篮球通过尼龙线提供的（小物体受到的重力与拉力相比可忽略），表明其所需的向心力在变大。

那么，物体做圆周运动时所需的向心力与物体质量、转动半径以及角速度之间有着怎样的关系呢？下面我们通过实验来探究。

实验目的

探究做圆周运动的物体所需要的向心力 F 与其质量 m、转动半径 r 和转动角速度 ω 之间的关系。

实验器材

向心力演示器、小球等。

实验原理与设计

如图 3-15 所示，匀速转动手柄，可使塔轮、长槽和短槽匀速转动，槽内的小球也就随之做匀速圆周运动。挡板对小球的作用力提供了小球做匀速圆周运动的向心力。同时，小球挤压挡板的力使挡板另一端压缩测力套筒的弹簧，压缩量可从标尺上读出，该读数即显示了向心力的大小。如何研究向心力与物体质量、转动半径以及角速度之间的关系？

安全警示

快速转动手柄时，注意扶住实验装置，以免其倾覆，同时要防止小球从槽内甩出。

实验步骤

（1）把两个质量不同的小球分别放在长槽和短槽上，调整塔轮上的皮带和小球位置，使两球的转动半径和角速度都相同。转动手柄，观察向心力的大小与质量的关系。

（2）换两个质量相同的小球，使两球的角速度相同。再增大长槽上小球的转动半径，使两球的转动半径不同。转动手柄，观察向心力的大小与半径的关系。

（3）若要研究向心力的大小与角速度的关系，请按照你设计的实验步骤操作。

数据分析

请记录实验现象，分析实验中得到的向心力大小与物体质量、转动半径及角速度的关系。

实验结论

请写出实验结论。

讨论

在探究影响向心力大小的因素时，为何要注意控制变量？请通过日常生活中的案例，说明控制变量的重要性。

方法点拨

实验应采用控制变量法进行探究。在改变某个因素（如半径）的同时，必须控制其他因素（如质量和角速度）不变，以便于找出这个因素影响向心力变化的规律。

进一步研究得出，向心力的大小为

\[F = mr{\omega ^2}\]

如果将 ω＝\(\frac{v}{r}\)代入上式，可得

\[F = m\frac{{{v^2}}}{r}\]

素养提升

能分析物理现象，提出可探究的物理问题；能在他人帮助下采用控制变量的方法设计相关的探究方案，解决问题，能通过向心力演示仪等器材获得证据；能分析归纳实验信息、形成与实验目的相关的结论，作出解释；能撰写比较完整的实验报告，在报告中能呈现设计的实验步骤、实验表格、分析过程及实验结论，能根据实验报告进行交流。

注意提升实验设计能力及分析归纳能力。

——科学探究

DIS实验室

探究影响向心力大小的因素

我们还可用如图 3-16 所示的 DIS 向心力实验器来进一步定量探究影响向心力大小的因素。实验中，通过力传感器测出向心力 F 的大小，通过光电门传感器测量挡光杆的挡光时间，进而求出角速度 ω 的大小。借助 DIS 数据采集器以及计算机等工具分析 F 与 m、r、ω 之间的定量关系。

3．向心加速度

力是产生加速度的原因。既然做圆周运动的物体受到向心力的作用，那么它必然存在一个由向心力产生的加速度，这个加速度称为向心加速度（centripetal acceleration）。向心加速度的方向与向心力的方向一致，始终指向圆心。

根据牛顿第二定律和向心力公式，可以得到向心加速度的大小，即

\[a = r{\omega ^2}\qquad a = \frac{{{v^2}}}{r}\]

对于某一确定的匀速圆周运动，向心力和向心加速度的大小恒定不变，但方向却时刻在改变。因此，匀速圆周运动是加速度方向不断改变的变加速运动。

向心力和向心加速度的公式不仅适用于匀速圆周运动，而且适用于非匀速圆周运动。一般圆周运动的速度大小变化时，向心力和向心加速度的大小也会发生变化。利用公式求质点在某时刻或某位置的向心力和向心加速度的大小，其速度必须用该质点在该时刻或该位置的瞬时速度。

拓展一步

向心加速度的理论推导

设一质点沿着半径为 r 的圆周做匀速圆周运动，如图 3-17（a）所示。在某时刻该质点位于 A 点，经过很短一段时间 Δt 运动到 B 点。在此期间，质点的速度由v_A 变为 v_B ，速度改变量为 Δv 。若把速度矢量 v_B 的始端移到 A 点，其矢量关系如图3-17 （b）所示。

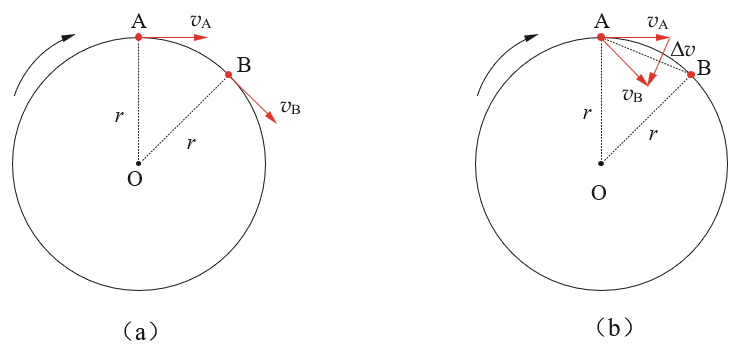
从图 3-17（b）可以看出，速度矢量三角形与相应的△OAB 是相似三角形，且v_A 和 v_B 的大小都等于线速度 v。用 Δs 表示 AB 弦长，有

\[\frac{{\Delta v}}{v} = \frac{{\Delta s}}{r}\]

即

\[\Delta v = \Delta s\frac{v}{r}\]

Δt 趋于零时，AB 弦长等于 AB 弧长，因此\(\frac{{\Delta s}}{{\Delta t}}\)等于线速度的大小 v。

Δt 趋于零时，\(\frac{{\Delta v}}{{\Delta t}}\)表示的就是向心加速度 a 的大小，且有\(\frac{{\Delta v}}{{\Delta t}} = \frac{v}{r} \cdot \frac{{\Delta s}}{{\Delta t}}\)，因此

\[a = \frac{{{v^2}}}{r}\]

再由 Δt 趋于零时， v_A 和 v_B 的夹角趋于零，Δv 的方向趋于与 v_A 垂直而指向圆心，即加速度的方向指向圆心。这样，就通过理论分析得到了向心加速度的大小和方向。

例题

一般飞行员能承受的最大向心加速度的大小约为 6g。在飞行表演中，飞机某次水平转弯时，可视为在水平面内做匀速圆周运动。若飞机以 150 m/s 的速度飞行，在该次水平转弯过程中向心加速度为 6g，取重力加速度 g = 9.8 m/s² ，飞机水平转弯半径至少为多少？

分析

飞机在转弯的过程中做匀速圆周运动，圆周运动的向心加速度与线速度及转弯半径有关，可根据向心加速度公式求解。

解

由题意可知，v = 150 m/s， a = 6g = 6×9.8 m/s² = 58.8 m/s²。

由 \(a = \frac{{{v^2}}}{r}\) 得

\[r = \frac{{{v^2}}}{a} = \frac{{{{150}^2}}}{{58.8}}{\rm{m}} = 382.7{\rm{m}}\]

讨论

飞机转弯半径与线速度和向心加速度有关。此题的转弯半径是针对比较极端情况的结果。对于客机，转弯半径的设计须考虑安全系数及乘客的舒适度等诸多因素，转弯半径通常较大。

策略提炼

认清向心加速度与线速度、角速度及半径的关系是解决此类问题的关键。注意根据已知量，选择恰当公式，求解未知量。

迁移

向心加速度由向心力产生。下面请分析解决涉及圆周运动的一些动力学问题。

在图 3-13 中，若水平圆台转动的角速度 ω = 0.6 rad/s，质量为 30 kg 的小孩坐在距离轴心 1 m 处随圆台一起转动。小孩的向心加速度为多大？小孩受到的静摩擦力为多大？

节练习

1．请撰写“探究向心力大小与半径、角速度、质量的关系”的实验报告，注意在报告中呈现设计的实验步骤、实验表格以及分析过程和实验结论。

2．在班级晚会上，有同学做了用杯子搬运乒乓球的游戏。如图所示，他用杯子扣住乒乓球快速摇晃，使球在杯壁内侧转动而不掉下来，成功地把乒乓球移动到了书的另一侧。请分析乒乓球没有掉下来的原因。

【解答】乒乓球受到重力和瓶壁的支持力，这两个力的合力为乒乓球做圆周运动提供向心力，所以乒乓球不会掉下来。

3．分析图中物体 A、B、C 的受力情况，并说明这些物体做圆周运动时由哪些力来提供向心力？

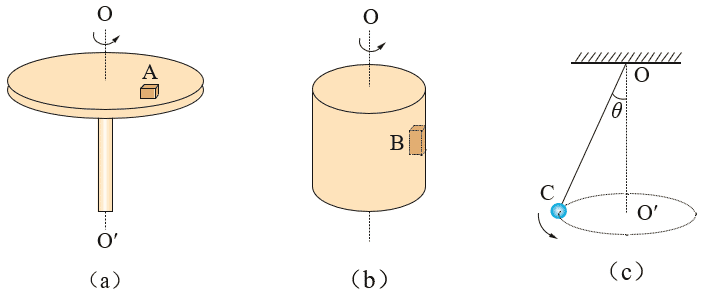
【解答】（a）静摩擦力提供向心力；（b）筒壁对物体的压力提供向心力；（a）绳对小球的拉力的水平分力提供向心力。

4．关于匀速圆周运动，下列说法正确的是

A．匀速圆周运动是匀速运动                   B．匀速圆周运动是匀变速运动

C．匀速圆周运动是匀速率圆周运动        D．在任意相等的时间内通过的路程相等

【CD】

5．太阳的质量为 1.99×10³⁰ kg，距银河系中心约 3 万光年（1 光年≈ 9.46×10¹² km），以 220 km/s左右的速率绕银河系中心转动。试计算太阳绕银河系中心转动时所需向心力的大小。

【解答】3.39×1020 N

6．在探究向心力大小与半径、角速度、质量的关系的实验中，若用两个质量相等的小球做实验，且左边小球的轨道半径为右边小球的 2 倍，转动时发现右边标尺上读取的向心力的大小是左边的 2 倍。那么，左边小球与右边小球的角速度之比是多少？

【解答】1∶2

7．如图所示，长为 l 的悬线一端固定在 O 点，另一端系一小球。在 O 点正下方 C 点钉一钉子，O、C 间距离为\(\frac{l}{2}\)。把悬线另一端的小球拉到跟悬点同一水平面上无初速度释放，小球运动到悬点正下方时悬线碰到钉子，则小球的

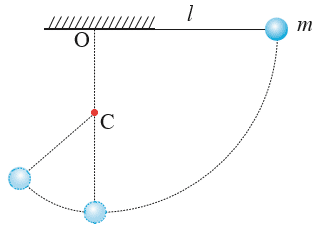
A．线速度突然增大为原来的 2 倍

B．角速度突然增大为原来的 2 倍

C．向心加速度突然增大为原来的 2 倍

D．悬线拉力突然增大为原来的 2 倍

【BC】

发布时间：2021/2/22 下午9:36:43  阅读次数：5493