第五章 第二节 平抛运动

图 5–11 黄果树瀑布
黄果树瀑布是我国著名景点之一。利用黄果树瀑布的照片引出平抛运动的情境,能使学生初步感知什么是平抛运动,以及平抛运动的轨迹形状和运动特点。这正是本节要讨论的重点。
本节编写思路
本节通过节首图瀑布顶端飞出的水滴,以及上抛的乒乓球、水平击出的排球、斜向上踢出的足球等所做的运动引出抛体运动的概念,进而提出平抛运动的概念。用生活中常见的事例引出本节讨论的主题,建立平抛运动的概念,对学生而言是比较直观的。
通过“平抛运动有什么规律?”的问题,引导学生根据运动合成与分解的思想探究平抛运动的特点,并根据数据分析结果归纳得出结论。依据实验结论,运用运动合成与分解的方法,通过演绎推理,得到平抛运动的位移和速度的规律。
生活中很多熟悉的运动都可以被视为抛体运动。经历平抛运动规律的探究过程将提升从实验中获取信息、处理信息,以及归纳实验结论的能力,体会物理学中实验探究和理论推导的方法,以及化繁为简的研究方法。
学习过程中经历的观察、实验、思辨等过程,有助于学生掌握运动规律和研究方法,并用来解释和描述常见的平抛运动,为日常生产生活提供指导。
如图 5–12 所示,将乒乓球向上抛出,将排球水平击出,将足球斜向踢出,这种以一定速度抛出,在空气阻力可以忽略、只在重力作用下的运动叫做抛体运动。若抛出物体的初速度沿水平方向,该物体的运动叫做平抛运动,图 5–11 中瀑布顶端飞出的水滴,图 5–12(b)中水平击出的排球所做的运动,都可以近似看作平抛运动。

(a)

(b)

(c)
图 5–12 常见的抛体运动
复杂的曲线运动可以看成是两个或多个简单运动的合成,下面,我们用运动合成与分解的方法通过实验来探究平抛运动的规律。
探究平抛运动的特点
“探究平抛运动的特点”的实验由两部分内容组成,分别为探究平抛运动竖直方向分运动的规律和探究平抛运动水平方向分运动的规律。
教材图 5–13 所示的实验装置是通过比较平抛小球 A 和自由落体小球 B 的下落时间得出平抛运动竖直方向分运动的规律。开始实验前,弹性金属片所夹的小球 B 必须与小球 A 处在同一高度;摆锤敲击弹性金属片时必须使小球 A 和小球 B 同时开始运动。
教材图 5–14 所示的实验装置可以用来获取小球一次平抛运动的轨迹,然后分析小球的运动轨迹坐标,得出平抛运动水平方向分运动的规律。实验要注意的事项有:① 保证竖直板处于竖直平面内;② 保证小球水平抛出;③ 因为是研究小球的“一次”平抛运动,小球在斜槽上始须从同一位置由静止释放;④ 为精确描述平抛运动的轨迹,必须合理选取一定数量的落点位置。
此实验要注重对学生实验设计、实验观察、实验条件控制和实验操作技能的培养,通过此实验使学生进一步提升实验探究能力。
提出问题
平抛运动有何特点?
实验原理与方案
做平抛运动的物体初速度沿水平方向,只受重力作用,可以将平抛运动分解为水平和竖直方向上的两个直线运动来研究。
实验装置与方法
图 5–13 探究平抛运动
竖直方向分运动的规律
图 5–14 探究平抛运动
水平方向分运动的规律
如图 5–13 所示的装置包含摆锤、弹性金属片和两个小球。当摆锤敲击弹性金属片时,小球 A 和 B 同时开始运动,小球 A 由于受到水平撞击做平抛运动,而小球 B 从原地落下做自由落体运动。通过比较做平抛运动和自由落体运动的小球落地先后,探究平抛运动竖直方向分运动的规律。
如图 5–14 所示的装置包含底部水平的斜槽、可以固定方格纸和复写纸的竖直板,以及可以上下移动的带凹槽的挡板。当小球从斜槽水平飞出后落在挡板的凹槽中,由于小球受到凹槽的挤压会通过复写纸在方格纸上留下落点的位置。通过小球落点的位置轨迹,探究平抛运动水平方向分运动的规律。
实验操作与数据收集
(1)将摆锤拉开一定角度后释放,摆锤击中弹性金属片,记录两个小球落地的先后。分别改变摆锤的释放角度和小球距地面的高度,重复实验,将数据结果记录到表 5–1 中。
表 5–1 实验数据记录表
|
实验序号 |
1 |
2 |
3 |
4 |
5 |
|---|---|---|---|---|---|
|
两个小球落地的先后 |
|
|
|
|
|
(2)在竖直板上依次附上方格纸和复写纸,记录小球飞出点的位置,并标上水平方向和竖直方向。将挡板固定在某一高度,让小球由静止沿斜槽滚下,记录小球的落点位置;改变挡板的高度,使小球从斜槽的同一高度由静止滚下,再次记录小球的落点位置;重复实验,可以在方格纸上得到小球平抛运动过程中的多个落点位置。
数据分析
比较做平抛运动和自由落体运动的小球落地先后,归纳平抛运动竖直方向分运动的规律。
用平滑曲线连接各落点位置,得到小球做平抛运动的轨迹。以小球飞出点为原点,建立合适的平面直角坐标系。根据竖直方向分运动的规律,设法在轨迹上取一组时间间隔相等的点,根据这些点的坐标,分析平抛运动水平方向分运动的规律。
在数据分析时要注意:① 建立直角坐标系时,原点必须是小球抛出点的球心位置(不是斜槽底部的端点位置);② 根据实验记录的位置点拟合平抛运动轨迹时,要光滑连接各点形成一条平滑的曲线;③ 实验记录的小球各位置点并不是连续相等时间间隔的点,数据分析时,必须在上述获得的平滑曲线上,根据竖直方向自由落体的运动规律选取一组时间间隔相等的点作为数据分析点。
通过数据处理和分析可得到实验结论:平抛运动水平方向的分运动是匀速直线运动。
实验结论
平抛运动竖直方向上的分运动为___________;水平方向上的分运动为_________。
交流与讨论
各组就数据分析的具体过程进行交流,比较、分析实验结果的异同及其原因。
图 5–15 探究平抛运动的另一种装置
本实验也可选用如图 5–15 所示的装置,包含电磁定位板、弹射器、平抛物体(含信号源)、接球槽等。平抛物体被弹射器水平射出后,每隔相同的时间发射一次信号,电磁定位板接收信号并记录该时刻平抛物体的位置信息,通过计算机对采集到平抛物体的位置信息进行处理,即可得到平抛物体在水平方向和竖直方向分运动的规律。
采用电磁定位板是“探究平抛运动的特点”实验的另一方案,有条件的学校可以采用。实验操作时要注意:① 用水平仪调节电磁定位板上边沿至水平;② 平抛物体的顶盖面必须正对电磁定位板,即亮灯一面朝外,否则数据点的位置有漂移;③ 重复实验时,每次打开信号源后应重新设置零点位置;④ 平抛物体落入接球槽后,应避免反弹。
通过大量实验,我们发现平抛运动可以分解为水平方向的匀速直线运动和竖直方向的自由落体运动。可见,平抛运动的加速度就是重力加速度,所以平抛运动是一种匀变速曲线运动。
在学生实验得出结论的基础上,要强调平抛运动的加速度就是重力加速度,平抛运动是一种匀变速曲线运动。然后,运用数形结合的方法进行分析和演绎,进一步从理论上推演得出平抛运动的位移公式和位移方向规律。通过分析和演绎得出重要结论,有助于模型建构、科学推理能力的提高。
如图 5–16 所示,对一个做平抛运动的物体,我们以抛出点为坐标原点、水平抛出的初速度方向为 x 轴正方向、竖直向下为 y 轴正方向,建立直角坐标系。物体做平抛运动的规律就可以用 x 轴和 y 轴两个方向的分运动的规律来表示。
通常将物体由原点沿 x 轴正方向抛出的时刻作为初始时刻,则经过时间 t,做平抛运动的物体在 x 轴和 y 轴方向的分运动的位移随时间 t 变化的规律分别为
\[\color{#357A4A}{\begin{array}{l}x = {v_0}t\\y = \frac{1}{2}g{t^2}\end{array}}\]
物体做平抛运动的位移是这两个分运动位移的矢量和。根据平行四边形定则,位移的大小为
\[s = \sqrt {{x^2} + {y^2}} \]
位移方向可用其与 x 轴的夹角 α 表示,则
\[\tan \alpha = \frac{y}{x} = \frac{{gt}}{{2{v_0}}}\]
由于将抛出时刻作为初始时刻,做平抛运动的物体在任一时刻沿 x 轴和 y 轴两个分运动的速度大小分别为
\[\color{#357A4A}{\begin{array}{l}{v_x} = {v_0}\\{v_y} = gt\end{array}}\]
根据平行四边形定则,物体在该时刻的速度是两个分运动速度的矢量和,其大小为
同样,运用数形结合的方法进行分析和演绎,推演得出平抛运动的速度公式和速度方向规律。
\[v = \sqrt {v_x^2 + v_y^2} = \sqrt {v_0^2 + {{(gt)}^2}} \]
速度方向可用其与 x 轴的夹角 θ 表示,则
\[\tan \theta = \frac{{{v_y}}}{{{v_x}}} = \frac{{gt}}{{{v_0}}}\]
距地面相同高度,将几个物体以不同的初速度自同一点水平抛出,这些物体飞行的时间相等吗?
此处设置“大家谈”是为了在演绎平抛运动位移和速度的规律后进一步理解平抛运动的时间由高度决定,强化合运动与分运动具有独立性和等时性。
参考答案:这些物体飞行的时间相等。
根据平抛运动在 x 轴、y 轴两个方向分运动的位移公式 x = v0t、y = \(\frac{1}{2}\)gt2,消去时间 t,就可以得到 y 与 x 之间的关系:y = \(\frac{g}{{2v_0^2}}\)x2。在该式中,重力加速度 g 与平抛初速度 v0 都不随时间变化,即 \(\frac{g}{{2v_0^2}}\) 与 x、y 无关,因此,上式具有二次函数 y = ax2 的形式。数学中把二次函数的图像叫抛物线,就是从抛体运动而来的。
此处设置“拓展视野”是为了让学生了解平抛运动的轨迹是抛物线。平抛运动轨迹方程的得出主要是数学推演过程,在推演过程中要注意体现数形结合,更要注意从物理的角度理解平抛运动的轨迹方程。教师可根据学生情况提出问题:① 若初速度增大,轨迹形状会如何变化?② 若在重力加速度较小的环境中,轨迹形状又将如何变化?
示例 如图 5–17 所示,一架小型运输机以 v0 = 180 km/h 的速度水平飞行,在 h = 320 m 高空向灾区投放救灾物资包。(不计空气阻力,g 取 10 m/s2)
例题的设置是为了让学生认识平抛运动的普遍性,体会物理学在实际生活中的应用价值。例题示范的教学过程是在教师的引导下,提炼出解决问题的程序和规范,让学生逐步提升运用物理规律解决实际问题的能力。
图 5–17 空投物资包
(1)为了将物资包准确投到目标位置,应当在离该位置的水平距离多远处释放物资包?
(2)物资包落地时,速度的大小和方向如何?
分析:救灾物资包做平抛远动。运用运动分解的方法,可以先算出物资包在竖直方向分运动(自由落体运动)的时间,这就是物资包平抛运动的飞行时间,也是水平方向运动的时间。在这段时间内,运输机水平匀速飞行的距离就是释放物资包的位置与目标位置之间的水平距离。
解:(1)物资包被投放后做平抛运动。建立如图 5–17 所示的坐标系,根据平抛运动在竖直方向分运动的规律,物资包在竖直方向的位移 y 与其运动时间 t 的关系为
解这类题的基本过程是:① 对研究对象进行运动和受力分析,确定其满足做平抛运动的条件;② 建立直角坐标系;③ 在两个分运动的方向上,分别运用运动学公式建立适当的方程,并得出相应的结果;④ 对分运动进行合成,得到最终结果;⑤ 对得到的结果是否合理进行论证。
\[y = \frac{1}{2}g{t^2}\]
当 y = h 时,物资包落到地面,可知救灾物资包的飞行时间
\[t = \sqrt {\frac{{2y}}{g}} = \sqrt {\frac{{2h}}{g}} = \sqrt {\frac{{2 \times 320}}{{10}}}\; {\rm{s}} = 8\;{\rm{s}}\]
根据平抛运动在水平方向分运动的规律,可知物资包投放后到达目标位置的水平位移
\[x = {v_0}t\]
又 v0 = 180 km/h = 50 m/s,得
\[x = 50 \times 8\;{\rm{m}} = 400\;{\rm{m}}\]
所以,为准确地将物资包投送到目标位置,应当在离目标位置水平距离 400 m 处提前投放。
(2)物资包落地时速度的水平分量和竖直分量的大小分别为
\[{v_x} = {v_0},{v_y} = gt = \sqrt {2gh} \]
因此,物资包落地的速度大小为
\[v = \sqrt {v_x^2 + v_y^2} = \sqrt {v_0^2 + 2gh} \]
代入数据,得
\[v = \sqrt {{{ 50}^2} + 2 \times 10 \times 320} \;{\rm{m/s}} \approx 94.3\;{\rm{m/s}}\]
物资包落地时速度的方向与水平方向夹角 θ 的正切为
\[\tan \theta = \frac{{{v_y }}}{{{v_x}}} = \frac{{\sqrt {2gh} }}{{{v_0}}}\]
代入数据,得
\[\tan \theta = \frac{{\sqrt {2 \times 10 \times 320} }}{{50}} = 1.6\]
故 θ ≈ 58°
因此,救灾物资包落地时速度的大小为 94.3 m/s,速度的方向与水平面的夹角约为 58°。
上例分析中忽略了空气阻力的影响。实际的空投作业往往是一项复杂的、需要综合考虑各种因素的工作。如果飞机飞得比较高,救灾物资包会因为落地速度很大而受损。为安全地实施空投,你能否给出一些设想和方案?
此处设置“大家谈”是为了让学生了解实际的抛体运动往往比较复杂,在运用平抛运动规律解释和解决生产生活中的实际问题时,常需要忽略一些次要因素,是理想化的。这里的问题是开放的,会有多种回答。
- 判断下列物体的运动是否属于抛体运动,并说明理由
(1)洒水车喷出的水。
(2)运动员推出的铅球?
(3)向空中抛出的一张纸。
(4)竖直向下扔出的一粒石子。
(5)运动员发球时竖直向上抛出的网球。
图 5–18
- 做平抛运动的物体在任意 1 s 内速度变化量的大小是多少?方向如何?
- 水平匀速飞行的飞机上连续投下一系列物体,站在地面上的人看到的情景是否如图 5–18 所示?飞机上的人看到的又是怎样的情景?
- 极限运动员想驾驶摩托车以 30 m/s 的水平初速度做飞越河谷表演,河谷的尺寸如图 5–19 所示。不计空气阻力,摩托车能否越过该河谷?简述理由。
- 以初速度 v0 水平抛出一小球,忽略空气阻力。如图 5–20 所示,某同学画出了该小球经历连续相等时间后速度矢量 v1、v2、v3 的关系图。对该同学所画的图作出评价?
- 在“ 探究平抛运动的特点” 实验中,某同学得到了如图 5–21 所示的数据轨迹线,则该平抛运动的初速度大小为多少?
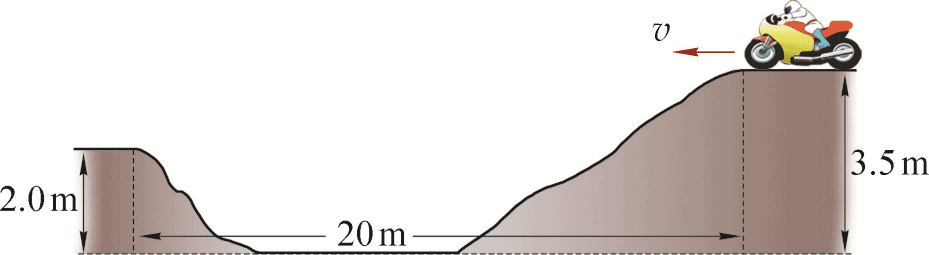
图 5–19
图 5–20
图 5–21
- 奥运会 50 m 步枪射击项目所用靶的直径为 154.4 mm。如图 5–22 所示,若某步枪运动员沿水平方向射击,正好对准靶的中心。分析说明:
(1)若子弹飞出枪膛的速度为 600 m/s,能否击中靶?
(2)若子弹飞出枪膛的速度为 350 m/s,能否击中靶?
(3)实际射击时,运动员应该如何瞄准才能取得更好的成绩?
图 5–22
问题与思考解读
1.参考解答:(1)(2)(4)(5)中物体的运动可以忽略空气阻力的影响,可看作只受重力作用,属于抛体运动;(3)中的纸张不可忽略空气阻力的作用,不属于抛体运动。
命题意图:根据对实际事例的分析,加深理解物体做抛体运动的条件。
主要素养与水平:运动与相互作用(Ⅰ);模型建构(Ⅰ)。
2.参考解答:物体做平抛运动的加速度为重力加速度 g = 9.8 m/s2,所以其任意 1 s 内速度变化量的大小为 9.8 m/s,方向竖直向下
命题意图:对平抛运动的条件形成有进一步的认识。
主要素养与水平:运动与相互作用(Ⅰ);科学推理(Ⅰ)。
3.参考解答:是。飞机上的人只看到最后投出的物体,之前投出的物体均被最后一个物体挡住(这些物体处在同一条竖直线上)。
命题意图:理解平抛运动在水平方向的分运动为匀速直线运动,在竖直方向的分运动为自由落体运动。
主要素养与水平:运动与相互作用(Ⅰ);模型建构(Ⅱ);科学椎理(Ⅱ)。
4.参考解答:飞越河谷到对岸其竖直高度差为 h = (3.5 – 2.0) m = 1.5 m,则根据 h = \(\frac{1}{2}\)gt2 得飞越时间 t = \(\sqrt {\frac{{2h}}{g}} \) ≈ 0.55 s,如果以 30 m/s 的水平初速度飞越河谷,飞跃的水平距离 s = v0t = 16.5 m,小于河谷的宽度 20 m,所以摩托车不能越过该河谷。
命题意图:从题设条件中提取有用的信息,建立平抛运动模型,讨论实际问题。
主要素养与水平:模型建构(Ⅰ);科学论证(Ⅱ);科学本质(Ⅰ)。
5.参考解答:该图有错。平抛运动水平方向分运动为匀速直线运动,水平方向的分速度不变,故图中各时刻速度矢量末端在同一竖直线上是正确的。但因平抛运动竖直方向的分运动是自由落体运动,在相等时间内速度的增加量是相等的,即图中小球经历连续相等时间后的速度矢量 v1、v2、v3 末端在竖直方向的间隔应该相等,所以该图有错。
命题意图:根据平抛运动的规律,判断速度矢量之间的关系。强化竖直方向分运动的规律。
主要素养与水平:运动与相互作用(Ⅱ);模型建构(Ⅱ);质疑创新(Ⅱ)。
6.参考解答:由题设数据分析得,坐标原点 O 为平抛运动的抛出点。根据 y = \(\frac{1}{2}\)gt2,x = v0t,得平抛运动的初速度为 v0 = x\(\sqrt {\frac{g}{{2y}}} \) ≈ 1.58 m/s。
命题意图:通过对实验数据的分析,判断物体的运动性质及运动状态,提升物理实验数据分析的能力。
主要素养与水平:证据(Ⅱ);解释(Ⅱ)。
7.参考解答:若忽略子弹飞行时空气阻力的影响,则子弹在空中的运动是平抛运动。根据平抛运动的规律,其水平方向分运动为匀速直线运动 x = v0t,竖直方向分运动为自由落体运动 y = \(\frac{1}{2}\)gt2,亦即 y = 2g\({\left( {\frac{x}{{{v_0}}}} \right)^2}\)。(1)代入数据,得 y1 ≈ 0.034 m = 34 mm,小于靶的半径,所以能击中靶。
(2)代入数据,得 y2 = 0.10 m = 100 mm,大于靶的半径,所以不能击中靶。
(3)为使子弹击中靶心,运动员瞄准时应考虑子弹飞行时竖直方向有下落的效果,所以应瞄准比靶心略高处。
命题意图:将射击运动中子弹的实际运动抽象为满足条件的平抛运动,体验基于经验事实与物理原理建构物理模型的思想,联系实际学以致用。
主要素养与水平:模型建构(Ⅲ);科学推理(Ⅲ);科学论证(Ⅲ);科学本质(Ⅱ)。
发布时间:2022/2/1 下午2:58:19 阅读次数:10052
