第一章 第四节 速度变化的快慢 加速度

图 1–28 运动员起跑瞬间
观察照片中运动员的位置和拖影,在相同曝光时间内,冲在前面的运动员跑过的距离长,起跑的速度快。因默认所有运动员均同时从静止出发,还可以知道在相同时间内冲在前面的运动员速度的增加量大,从而认识速度变化的快慢是变速直线运动的重要表征。
本节利用实际物体运动及速度变化的数据,通过“自主活动”“示例”建立速度变化、速度变化快慢的概念,并进而定义“加速度”。
通过对汽车加速测试数据的分析和“自主活动”,了解如何由 v–t 图像得到加速度,加深对变化率概念的理解。
通过对汽车加速和减速过程的具体计算与分析,理解加速度的矢量性和在一维运动情况下的表示方法。
学习中经历的从现象、数据到加速度概念建立的过程是对由具体到抽象思维过程的训练,并有助于形成完整的运动观念。
如图 1–28 所示,发令枪响,短跑运动员们似离弦之箭冲出起跑线,有的运动员冲到了前面,这说明他的速度增加得比其他运动员快。赛车从静止加速到 100 km/h 仅需 2.5 s 左右,所需时间不到一般家用轿车从静止加速到 100 km/h 所用时间的四分之一。这两个事例说明不同的变速运动中速度变化的快慢往往是不同的。如何描述做变速直线运动物体速度变化的快慢呢?
飞机以 200 m/s 的速度沿直线匀速飞行;运载火箭点火后竖直升空,2 s 内由 0 m/s 加速到 60 m/s;赛车沿直线赛道启动,从静止加速到 100 km/h 约需 2.5 s。
以上三种情况中:
(1)哪个物体的速度变化量最大?哪个物体的速度变化量最小?
(2)哪个物体的速度变化最快?哪个物体的速度变化最慢?
说出你的依据。
此处设置“大家谈”的目的是理解速度变化量 Δv 与速度变化快慢 \(\frac{{\Delta v}}{{\Delta t}}\)的不同含义。知道速度变化快慢可以用单位时间内的速度变化量表征。
飞机 Δv = 0,\(\frac{{\Delta v}}{{\Delta t}}\)= 0;火箭 Δv = 60 m/s,\(\frac{{\Delta v}}{{\Delta t}}\) = \(\frac{{60}}{2}\) m/s2 = 30 m/s2;赛车 Δv = 100 km/h = 27.8 m/s,\(\frac{{\Delta v}}{{\Delta t}}\) = \(\frac{{27.8}}{2.5}\) m/s2 = 11.1 m/s2。结合下一页的“大家谈”可以进一步明确:加速度大小与速度大小、速度变化量的大小表示的物理意义不同,它们之间没有直接关系。
做变速直线运动的物体在相等时间内速度变化量越大,速度变化越快。描述物体速度变化的快慢需要同时考虑速度变化量 Δv 与发生这一变化所用的时间 Δt。物理学中用速度的变化量 Δv 与发生这一变化所用时间 Δt 的比表示速度变化的快慢,称为加速度(acceleration),通常用字母 a 表示。加速度是速度随时间的变化率。
\[\color{#035C87} a = \frac{{\Delta v}}{{\Delta t}}\]
某个量 D 的变化量可记为 ΔD,如果发生这个变化所用的时间为 Δt,则 ΔD 与 Δt 的比 \(\frac{{\Delta D}}{{\Delta t}}\) 称为 D 的变化率。速度是位置的变化率,加速度是速度的变化率。变化率表示变化的快慢。
“拓展视野”介绍了变化率。
在数学上,任一随时间变化的量 y(t)随时间变化的快慢程度可以用其变化率 \(\frac{{\Delta y(t)}}{{\Delta t}}\) 表示。但在物理学中,是否需要将某物理量的变化率定义为新的物理量,需考虑是否具有物理意义。
譬如,我们用物体位置(或相对原点的位移)x 的时间变化率 \(\frac{{\Delta x}}{{\Delta t}}\)表示物体运动的快慢,从而定义了一个新的物理量——速度;同理,我们定义加速度 a = \(\frac{{\Delta v}}{{\Delta t}}\)表示速度变化的快慢。实际上,运动物体的加速度 a 往往也是随时间变化的,在物理学中并没有进一步将加速度的变化率 \(\frac{{\Delta a}}{{\Delta t}}\) 定义为一个新的物理量,其原因是根据牛顿运动定律,在质量一定的情况下,只要知道物体的受力,就可以知道其加速度,从而确定其运动情况,因此,在物理学范畴中无需再定义新的物理量。
但在工程领域,加速度变化的快慢,即“加加速度”是一个有意义的量,称为“急动度”。汽车高速匀速行驶时,乘客的唯一感受是窗外物体飞速掠过,如果汽车突然加速或减速,乘客便会后仰或前冲,引起不舒服的感觉。在工程上通常用急动度描述人的不舒适程度,这在设计交通工具时是一个需要考虑的因素。
若物体在初时刻 t1 的速度为 v1 ,末时刻 t2 的速度为 v2,则在 Δt = t2 − t1 的时间内物体速度的变化量为 Δv = v2 − v1,物体的加速度可表示为
\[\color{#035C87} a = \frac{{\Delta v}}{{\Delta t}} = \frac{{{v_2} - {v_1}}}{{{t_2} - {t_1}}}\]
在国际单位制中,加速度的单位是米/秒2(m/s2 或 m·s−2),读作“米每二次方秒”。
物体的速度很大,加速度就一定很大吗?物体速度的变化量很小,加速度就一定很小吗?
承接上一页的“大家谈”,通过讨论来辨析速度、速度变化量和加速度。
表 1–6 某新型轿车的部分参数
|
功率 P/kW |
301 |
|
百公里加速时间 t/s |
6.71 |
|
最高速度 v/(km·h−1) |
265 |
示例 汽车的“百公里加速时间”是反映汽车动力性能的重要指标。表 1–6 为某新型轿车的部分参数,求该车从静正加速到 100 km/h 的加速度大小。
车在从静止开始做加速运动的过程中,加速度是随速度的增大逐渐减小的。这里求出的加速度实际上是车在“百公里加速时间”内的平均加速度,表示在这段时间内轿车加速的平均快慢程度。
这里处理问题的思路是把车的加速过程简化为加速度恒定的过程,实际上就是抽象为理想化模型的处理方法。
分析:汽车的“百公里加速时间”指的是该车从静止起加速到 100 km/h 所需要的时间 t。把车抽象为质点,假设汽车在加速过程中沿直线运动,根据加速度的定义,利用表中参数可以求得该车的加速度大小。
解:以汽车为对象,设启动时刻 t1 = 0 s ,此时汽车的初速度大小 v1 = 0 m/s 。由表 1–7 中的数据可知,在 t2 = 6.71 s 的时刻汽车加速到 100 km/h ,此时汽车的速度大小 v2 = 100 km/h ≈ 27.8 m/s 。
根据加速度的定义可得,该车由静止加速到 100 km/h 的加速度 a 大小为
\[a = \frac{{\Delta v}}{{\Delta t}} = \frac{{{v_2} - {v_1}}}{{{t_2} - {t_1}}} = \frac{{27.8{\rm{m/s}} - 0{\rm{m/s}}}}{{6.71{\rm{s}} - 0{\rm{s}}}} \approx 4.14{\rm{m/s}}\]
表 1–7 中数据反映了一些物体加速度大小的数量级。
表 1–7 一些物体加速度大小的数量级[ a/ (m·s−2)]
|
物体 |
加速度大小的数量级 |
|---|---|
|
加速器中的质子 |
1015 |
|
击发后枪膛中的子弹 |
105 |
|
离弦前的箭 |
103 |
|
点火升空时的火箭 |
102 |
|
地球上的自由落体 |
10 |
|
月球上的自由落体 |
100 |
|
启动时的列车 |
10−1 |
|
起航时的万吨货轮 |
10−2 |
与速度有平均速度、瞬时速度之分类似,加速度也有平均加速度和瞬时加速度。
一般而言,物体做变速运动时速度变化的快慢程度也会随时间和空间位置而变化。此时,速度的变化量 Δv 与所用时间 Δt 的比即为该段时间内的平均加速度。平均加速度只能粗略地表示某段时间内物体速度变化的快慢程度。
如果 Δt 无限趋近于 0,即得到某一时刻速度的瞬时变化率,相应的加速度称为瞬时加速度。瞬时加速度描述了物体在某时刻、经过相应位置速度变化的快慢。
“拓展视野”介绍了平均加速度和瞬时加速度。物体在实际运动时不仅速度随时间变化,加速度通常也在随时间变化。与速度概念类似,加速度也有平均加速度与瞬时加速度之分。
如果物体的速度随时间均匀变化,即加速度不随时间变化,物体在各段时间的平均加速度与各个时刻的瞬时加速度都相等。此时,可不区分平均加速度和瞬时加速度而统称加速度。
图 1–29 某品牌汽车0–100 km/h 的 v–t 图像
加速度是反映汽车动力性能的一个重要指标。图 1–29 所示为某品牌汽车动力性能测试所得的 v–t 图像。在图像上选取相距较远的两点 A(v1,t1)、 B(v2,t2)。由此可以估算汽车在 t1 ~ t2 时间内的加速度的大小
\[a = \frac{{{v_2} - {v_1}}}{{{t_2} - {t_1}}}\]
观察反映汽车加速性能的 v–t 图像可知,在 0 ~ 3 s 时间段图像几乎为直线,速度随时间线性增大,加速度约为 20 m/s2,3 ~ 4.5 s 时间段图像逐渐向下弯曲,加速度约为 12.7 m/s2,4.5 ~ 6.5 s 时间段图像又几乎为直线,加速度约为 9 m/s2;可见,加速度在不同时间段并不相等,在整个加速过程中平均加速度约为 14.9 m/s2。
由此可进一步领略用图像描述物体运动的方法,深化对速度–时间图像意义的理解,提高从图像上读取、分析物体运动信息的能力。并为用 DIS 测量做变速直线运动物体的加速度奠定测量原理与方法的基础。
图 1–30 测量小车的加速度
在图 1–30 所示的装置中,小车沿斜导轨向下运动。利用分体式位移传感器获得小车运动过程中各个时刻的位移,经计算机对数据处理后得到小车速度随时间的变化。根据数据,在坐标平面上描点后连线,得到小车的 v–t 图像。由图像中的信息,估算小车的加速度大小。
通过“自主活动”初步了解匀加速直线运动的 v–t 图像,理解由图像获得小车加速度的方法;学习分体式位移传感器的使用方法。通过改变轨道倾角,感受加速度对速度变化的影响。
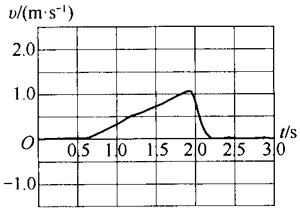
如图所示为实验所得小车沿倾斜导轨向下运动的 v–t 图像。在图像上选取线性关系明显的一段,通过图像的斜率测得小车的加速度大小。通过动手实验和分组交流,提高实验操作的技能和图像分析的能力,增强团队合作意识,培养认真细致、实事求是的态度。
小车沿导轨向下运动时,其速度方向沿导轨向下。若导轨倾角不同,小车由静止起加速后的速度方向也不同。可见,速度的变化是有方向的,反映物体速度变化快慢的加速度也是一个有方向的矢量。
加速度与速度同为矢量。根据加速度的定义,加速度 a 的方向与速度变化量 Δv。
一辆沿直线行驶的汽车在 5 s 内速度由 15 m/s 增加到 25 m/s,在随后的 5 s 内速度减小到 15 m/s。如图 1–31 所示,取汽车前进方向为正方向,分别画出两段时间内的初速度与末速度矢量。
学习如何利用矢量示意图表示速度的变化量和加速度的方向。理解在直线运动中加速度的方向与速度、速度变化量之间的关系。知道加速度方向与速度方向一致或相反,分别表示物体做加速运动或减速运动。
图1–31 加速度方向与速度方向的关系
如图 1–31(a)所示,在第 1 个 5 s 内:汽车速度的变化量 Δv = v2 − v1 = 25 m/s − 15 m/s = 10 m/s,加速度 a = \(\frac{{\Delta v}}{{\Delta t}} = \frac{{10{\rm{m/s}}}}{{5{\rm{s}}}}\) = 2 m/s2。
如图 1–31(b)所示,在第 2 个 5 s 内:汽车速度的变化量 Δvʹ = v3 − v2 = 15 m/s − 25 m/s = − 10 m/s,加速度 aʹ = \(\frac{{\Delta v'}}{{\Delta t}} = \frac{{ - 10{\rm{m/s}}}}{{5{\rm{s}}}}\) = − 2 m/s2。
在这两个过程中,汽车加速度的大小(即 a 的绝对值)相同,但前者为正,后者为负,
加速度的正、负表示其方向与正方向相同或相反。由此可见,运动物体加速度的方向不一定与速度的方向一致。
在直线运动中,若物体的加速度与其速度方向相同,则表示物体的速度大小在增大,做加速运动;若物体的加速度与其速度方向相反,则表示物体的速度大小在减小,做减速运动。
- A、B 两车均做直线运动。A 车的速度从 0 增大到 30 km/h,B 车从 20 km/h 加速到 60 km/h,两辆车的速度分别变化了多少?哪辆车的加速度更大?
- 速度是用位置的变化 Δx 与发生这一变化所需的时间 Δt 的比来定义的。对同一物体来说 Δx 很大时,速度可以不变。加速度是用速度的变化量 Δv 与发生这一变化所需的时间 Δt 的比来定义的。举例说明,同一物体做变速直线运动过程中速度变化量 Δv 增大,但加速度不变。

图 1–32
- 某同学乘坐磁浮列车(图 1–32)时记录了列车内显示屏的数据,如表 1–8 所示。
试根据表中数据描述磁浮列车由静止加速到 430 km/h 的过程中加速度的大小是如何变化的。
表 1–8
|
序号 |
时刻 |
速度 v/(km·h−1) |
|---|---|---|
|
1 |
16 时 22 分 00 秒 |
0 |
|
2 |
16 时 22 分 40 秒 |
94 |
|
3 |
16 时 23 分 20 秒 |
170 |
|
4 |
16 时 24 分 00 秒 |
269 |
|
5 |
16 时 24 分 40 秒 |
355 |
|
6 |
16 时 25 分 20 秒 |
425 |
|
7 |
16 时 25 分 26 秒 |
430 |
|
8 |
16 时 26 分 00 秒 |
430 |
图 1–33
- 如图 1–33 所示,一个弹性小球在光滑水平面上以 5 m/s 的速度撞墙后,以大小不变的速度反向弹回。球与墙的接触时间为 0.005 s。用速度矢量表示撞墙前、后小球速度 v 和速度变化量 Δv,并求小球在与墙接触过程中的加速度 a。
- 舰载机陆地模拟训练时着舰速度约为 60 m/s,经过 8.5 s 后静止。舰载机的加速度为多大?方向如何?
- 某小车运动的 v–t 图像如图 1–34 所示。 t1 ~ t2、 t3 ~ t4 时间间隔内的 v–t 图像近似看作直线。这两段时间内,小车的加速度为多大?设小车运动方向为正方向, t1 ~ t2 时间内的加速度和 t3 ~ t4 时间内的加速度是正还是负?说明理由。
图 1–34
1.参考解答:30 km/h,40 km/h,无法判断哪辆车的加速度更大。加速度是物体在单位时间内的速度变化量,仅知道速度变化了多少不够,还需要知道车辆速度变化所用的时间。
命题意图:从速度到速度的变化,再到速度变化的快慢。通过具体的事例体会变化快慢与变化量的关系。
主要素养与水平:运动与相互作用(Ⅰ);科学推理(Ⅰ)。
2.参考解答:提示:鼓励学生用自己的语言表达。
命题意图:为后续学习匀变速运动做准备。对 1、2 两题从理论上做综合提升。
主要素养与水平:科学推理(Ⅱ);科学论证(Ⅱ)。
3.参考解答:提示:根据表中的数据仅能估算列车在每经过 40 s 时间的平均加速度,以此来粗略描述列车速度变化的快慢。
命题意图:利用图表信息求列车加速度,认识实际的变速运动中,不仅速度随时间变化,通常加速度也在随时间变化。进一步体会取相同时间描述物理量变化的方法。
主要素养与水平:科学推理(Ⅰ);证据(Ⅰ)。
4.参考解答:如图所示。100 m/s2,方向向右。
命题意图:从情境转换成可定量描述的数值。
主要素养与水平:运动与相互作用(Ⅰ);科学推理(Ⅱ)。
5.参考解答:7.06 m/s2,方向与速度方向相反
命题意图:定量计算,规范计算过程和步骤。
主要素养与水平:运动与相互作用(Ⅰ);科学推理(Ⅰ)。
6.参考解答:t1 ~ t2 时间内的加速度为 \(\frac{{{v_2} - {v_1}}}{{{t_2} - {t_1}}}\),方向为正。t3 ~ t4 时间内的加速度为 \(\frac{{{v_1} - {v_2}}}{{{t_4} - {t_3}}}\),方向为负。小车在 t1 ~ t2 时间间隔内,速度增大,加速度与速度方向相同,加速度与速度均为正。在 t3 ~ t4 时间内速度在减小,加速度与速度方向相反,速度方向始终为正,所以 t3 ~ t4 时间的加速度为负。
命题意图:学习将具体的情境抽象为图像,并会从图像中提取信息。
主要素养与水平:科学推理(Ⅱ);科学论证(Ⅱ)。
发布时间:2021/7/4 下午1:39:47 阅读次数:8795
