第 1 章 第 4 节 加速度

通常，物体运动的速度会发生变化，而且变化的快慢不一定相同。例如，某高速列车起动（图 1-24），速度由0增加到 300 km/h，约需 500 s；某轿车起动（图1-25），速度由0增加到 100 km/h，约需 8 s。想想看，对于高速列车和轿车，在起动过程中，哪个的速度变化更大？哪个的速度变化更快？

要比较速度变化的快慢程度，可比较在相同时间内速度变化的大小。在上述问题中，我们可通过计算速度变化与所用时间之比进行比较。

在高速列车加速起动过程中，速度变化与所用时间之比为 \(\frac{{300{\rm{km/h}} - 0}}{{500{\rm{s}}}}\)＝\(\frac{{0.167{\rm{m/s}}}}{{1{\rm{s}}}}\)，说明高速列车平均每秒速度的变化为 0.167 m/s。同理，在轿车加速起动过程中，速度变化与所用时间之比为 \(\frac{{3.47{\rm{m/s}}}}{{1{\rm{s}}}}\)，说明轿车平均每秒速度的变化为 3.47 m/s。

显然，虽然高速列车总体上速度变化较大，但轿车平均每秒速度变化比高速列车的要大，因此轿车的速度变化更快。

在物理学中，物体运动速度的变化跟发生这一变化所用时间之比，称为物体运动的加速度（acceleration），用字母 a 表示。

如果用v₀表示物体运动的初速度，v_t 表示末速度，则在时间 t 内物体运动速度的变化为 v_t－v₀，加速度 a 可用以下定义式表示：

\[a = \frac{{{v_t} - {v_0}}}{t}\]

加速度的单位由速度和时间的单位确定。若速度的单位是米/秒，时间的单位是秒，则加速度的单位是米/秒²，符号为 m/s²或 m·s^-2，读作“米每二次方秒”。加速度是矢量，其方向与速度变化的方向相同。物体做加速直线运动时，加速度方向与速度方向相同；物体做减速直线运动时，加速度方向与速度方向相反。与速度类似，加速度也有平均加速度和瞬时加速度之分，上述公式中得到的加速度实际是时间t内的平均加速度。如果瞬时加速度保持不变，这种运动称为匀变速运动。

建立了加速度的概念，就可用加速度来描述物体运动速度变化的快慢。

素养提升

能结合瞬时速度、加速度概念的建构，体会研究物理问题的极限方法和抽象思维的方法。

——科学思维

物理聊吧

（1）“上海磁悬浮列车的速度可达到 431 km/h [图1-26（a）]，它的加速度一定很大。”这一说法对吗？为什么？

（2）运载火箭在刚点火的短时间内速度很小[图1-26（b）]，它的加速度一定很小吗？

例题

猎豹以 2.0 km/h 的初速度做加速直线运动（图1-27），经 2 s 的时间，速度可达到 72 km/h。试求猎豹的加速度。

分析

猎豹的加速运动情况如图1-28所示。已知猎豹的初速度、末速度和时间，可运用加速度的定义式求解加速度。由于初速度、末速度和加速度都是矢量，运用加速度定义式时需选定正方向。

解

选定猎豹的初速度方向为正方向。由题意可知，v₀ ＝ 2.0 km/h ＝ 0.56 m/s，v_t ＝ 72 km/h ＝ 20 m/s，t ＝ 2 s。

由加速度的定义，得猎豹的加速度

\[\begin{array}{l}a = \frac{{{v_t} - {v_0}}}{t}\\ = \frac{{20{\rm{m/s}} - 0.56{\rm{m/s}}}}{{2{\rm{s}}}}\\ = 9.72{\rm{m/s^2}}\end{array}\]

猎豹的加速大小为 9.72 m/s²，方向与猎豹的速度方向相同。

讨论

求出的加速度为正值，表示加速度的方向与选定的正方向相同，即与猎豹的速度方向相同。由此题结果可知，猎豹的运动可达到较大的加速度。能以较大的加速度突然加速扑向猎物，是猎豹成功捕猎的关键。

策略提炼

加速度是矢量。求加速度，包含球加速的大小和方向。

在运用加速定义是前，需要选定正方向（一般选定初速度方向为正方向），以此确定初速度与末速度的正负；若与选定的正方向相同，带入正值计算；反之，则带入负值计算。

加速度值的正负表示方向。若加速度为正值，表示加速度方向与选定的正方向相同；若加速度为负值，表示加速度方向与选定的正方向相反。

物理在线 同学们可上网查询不同汽车（或动物）加速时能达到的最大加速度。

素养提升

能了解时间、位移、速度和加速度的内涵，初步了解标量和矢量；能将时间、位移、速度和加速等概念与生活中的相关现象联系起来。能从物理学的视角观察身边的运动现象。

——物理观念。

迁移

若物体做减速直线运动，又该如何求加速度？例如，一动车正以234 km/h的速度行驶，司机接收到减速行驶信号后采取制动措施，在40 s内使动车速度减小到162 km/h。请计算动车运动的加速度，并谈谈这样计算的理由。

节练习

1．某同学在学习加速度时有以下看法，请判断其是否正确并说明理由。

（1）加速度的方向就是速度的方向。

（2）加速度为正值，表示速度一定越来越大。

（3）加速度不断减小，速度可不断变大。

（4）加速度不断变大，速度可不断变小。

【解答】（1）错误。若物体做减速运动，则物体的加速度方向与速度方向相反。

（2）错误。正方向的规定可以是速度方向，也可以说速度的反方向。若规定速度的反方向为正方向，当加速度与速度方向相反时，加速度为正值，但物体是做减速运动，速度大小越来越小。

（3）正确。加速度方向与速度方向相同时，虽然加速度减少，但速度越来越大。

（4）正确。加速度方向与速度方向相反时，虽然加速度增大，但速度越来越小。

2．下列关于汽车运动的描述，可能发生的是

A．汽车在某一时刻速度很大，而加速度为 0

B．汽车的加速度方向与末速度方向相反

C．汽车速度变化量很大，而加速度较小

D．汽车加速度很大，而速度变化很慢

【解答】ABC

3．某同学以 3.5 m/ s 的速度向车站跑了一段时间后，发现时间充足。于是，他在 10 s 内把速度减小到了 1 m/s。求他在减速过程中的加速度。

【解答】－0.25 m/s²

4．如图所示，战斗机在出现某些紧急状况时，飞机弹射座椅能将飞行员连同座椅一起弹出舱外。在某次地面上进行的弹射实验中，弹射座椅在 0.2 s 内向上弹离飞机，弹离飞机时的速度为 16 m/s。求飞行员模型在弹离过程中的加速度。

【解答】80 m/s²

5．篮球以 10 m/s 的速度水平撞击篮板后，以 8 m/s 的速度反向弹回。若篮球与篮板接触的时间为 0.1 s，求篮球在这段时间内的加速度。

【解答】－180 m/s²

6．请试一试，在斜面上不同位置同时释放两个相同的钢球，如图所示它们滚下时会相互靠近还是远离？它们在同一时刻的速度是否相同？加速度又是否相同？请作出解释。

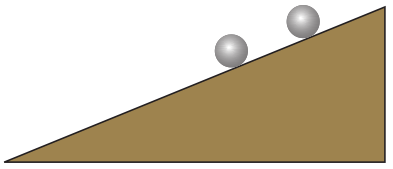
【解答】在斜面上不同位置同时释放两个相同的钢球，它们滚下时两球距离不变，因此，在任意时间内两球发生的位移相同，在任意时刻两球速度相同。又由于在任意时刻，两球速度相同，因此在任意时间内，两球速的变化相同，故在任意时刻，两球加速度相同。

发布时间：2021/5/5 下午3:10:47  阅读次数：2795