第一章 4 速度变化快慢的描述——加速度
一辆小汽车在 10 s 内，速度从 0 达到 100 km/h，一列火车在 300 s 内速度也从 0 达到 100 km/h。虽然汽车和火车速度都从 0 达到 100 km/h，但是它们的运动情况显然不同。你觉得用“速度大”或“速度变化大”能描述这种不同吗？如果不能，应该怎样描述呢？
小汽车和火车的速度都在增加，或者说两者都在做变速运动，并且它们的“速度变化”相同，但所用的时问不同。这两种情形的本质区别是“速度变化的快慢”不同。看来“速度变化的快慢”是一个不同于“速度”的概念。
两个物体速度变化相同，所用时间短的当然速度变化得快。如果两个物体速度变化不同，所用时间也不同，怎样比较它们速度变化的快慢呢？
在学习速度时我们知道，位移表示的是位置的变化。要比较位置变化的快慢，可以用位移除以时间。同理，要比较速度变化的快慢，可以用速度的变化量除以时间。
物理学中把速度的变化量与发生这一变化所用时间之比，叫作加速度（acceleration）。通常用 a 表示。若用 Δv 表示速度在时间 Δt 内的变化量，则有
在国际单位制中，加速度的单位是米每二次方秒，符
在这里，我们用两个物理量（速度的变化量和时间）之比定义了一个新的物理量——加速度，它的物理意义与原来的两个物理量不同。用两个物理量之比定义新的物理量是物理学中常用的方法。
号是 m/s 或 m·s−2。加速度是矢量，它既有大小，也有方向。现在讨论做直线运动的物体加速度的方向。
如图1.4–1，汽车原来的速度是 v1，经过一小段时间 Δt 之后，速度变为 v2。为了在图中表示加速度，我们以原来的速度 v1 的箭头端为起点，以后来的速度 v2 的箭头端为终点，作出一个新的有向线段，它就表示速度的变化量 Δv。由于加速度 a =
从图中可以看出，汽车在直线运动中，如果速度增加，即加速运动，加速度的方向与初速度的方向相同；如果速度减小，即减速运动，加速度的方向与初速度的方向相反。
对运动的物体而言，可以问“它运动了多远”，这是路程或位移的概念；也可以问“它运动得多快”，这是速度的概念，然而，在生活用语中，却没有与加速度对应的词语。
日常生活中一般只有笼统的“快”和“慢”，这里有时指的是速度，有时模模糊糊地指的是加速度。你能分别举出这样的例子吗？
v–t 图像反映的是物体的速度随时间变化的情况。你认为由 v–t 图像能知道物体的加速度吗？
图 1.4-2 中的两条直线 a、b 分别是两个物体 A 和 B 运动的 v–t 图像。E、F 两点所表示的时刻和速度分别为 t1、t2
和 v1、v2。从图中可以看出，小三角形的一条直角边代表时间隔 Δt，另一条直角边代表速度的变化量 Δv，Δv 与 Δt 的比为加速度，其比值为该直线的斜率。因此，由 v–t 图像中图线的倾斜程度可以判断加速度的大小。物体 A 的加速度比物体 B 的大。
生活中做变速运动的物体很多，它们加速度的大小也各不相同，有时差异还很大。下表为一些运动物体的加速度。
| 运动物体 | a/（m·s−2） | 运动物体 | a/（m·s−2） |
| 子弹在枪筒中 | 5×104 | 赛车起步 | 4.5 |
| 伞兵着陆 | − 25 | 汽车起步 | 2 |
| 汽车急刹车 | − 5 | 高铁起步 | 0.35 |
变化率
番茄在成熟的过程中，它的大小、含糖量等会随时间变化；树木在成长过程中，它的高度、树干的直径会随时间变化；河流、湖泊的水位会随时间变化；某种商品的价格会随时间变化；我国的人口生育量也会随时间变化……这些变化，有时快、有时慢j描述变化快慢的量就是变化率。
自然界中某量 D 的变化可以记为 ΔD，发生这个变化所用的时间间隔可以记为 Δt，变化量 ΔD 与 Δt 之比就是这个量对时间的变化率，简称变化率，显然，变化率在描述各种变化过程时起着非常重要的作用，速度和加速度就是两个很好的例子。
生活中还有哪些实例与变化率相关？例如飞机起飞时，在同样的时间间隔内，飞机的位移不断增大（图 1.4–3）。
某个量大，不表示它的变化率大。速度大，加速度不一定大。例如匀速飞行的高空侦察机，尽管它的速度可能接近 1 000 m/s，但它的加速度为 0。相反，速度小，加速度也可以很大。例如枪筒里的子弹，在开始运动时，尽管子弹的速度接近 0，但它的加速度可以达到 5×104 m/s2。
交通工具与社会发展
人类自发明木轮车（图 1.4–4）直到制成时速 500 km/h 的磁悬浮列车，以及超音速飞机，为了获得高速交通工具，奋斗了几千年，从某种意义上说，在人类发明的各种机械中，交通工具最深刻地改变了我们的生活，我们所用的物品，几乎没有一件不是由铁路或公路运输而来的。不难想象，如果没有了火车和汽车，现代社会将会瘫痪。
从世界各国的城市发展史上看，大城市规模的大小与车速的提高密切相关。大城市的直径一般就是当时最快的交通工具在 1 h 内行走的距离。以北京为例，清朝末年北京的“内城”大约是一个边长 5 km 的正方形，马车的速度大约就是 5 km/h；今天，有了发达的公路系统，有了快速轨道交通，汽车、城铁的速度大约是几十千米每时，北京城区的直径也扩大到了几十千米。
城市中的车速不能无限提高，城市的规模也就不能无限扩大。“摊大饼”式的城市规划可能带来以交通问题为主的许多矛盾。目前许多人认为，合理的发展模式是建立中心市区与卫星城组成的城市群。
运兵工具和武器运载工具的发展改变了战争的面貌。现代战争的“战场”已经与过去的意义完全不同、相距几千千米、几万千米的敌对力量之间很短时间内就能爆发大规模战争。空中打击的力量大大加强，过去的一些战术方法已经不再适用。由于车辆的使用，部队的机动性大大提高，速战速决的战争理论有所发展。
交通网络的形成大大缩短了不同地域的时空距离，促进了国与国、民族与民族之间的物资交流和人员往来，贸易上的互补，可以优化物质资源和人力资源的配置，促进世界经济的发展。不同文化的交融进一步促进了社会的进步。
然而，大量汽车带来了交通堵塞、频繁的事故、能源的过度消耗、尾气与噪声污染等一系列社会问题。这些不仅妨碍了人们的工作和生活，而且制约着社会经济的进一步发展。
如何处理这些矛盾，一直是人们努力探索的课题。随着可持续发展战略的实施，人们对发展交通的意义有了新的认识，采取了许多有效的措施。例如，研制各种绿色汽车（使用压缩天然气或液化石油气的汽车、太阳能车、电动车……），对现有汽车的使用在时间和道路上进行限制，根据城市规模发展地上、地下快速的立体化交通和轨道交通。
讨论：交通工具的速度是不是越快越好？
1．小型轿车从静止开始加速到 100 km/h 所用的最短时间，是反映汽车性能的重要参数。A、B、C 三种型号的轿车实测的结果分别为 11.3 s、13.2 s、15.5 s，分别计算它们在测试时的加速度有多大。
2．有没有符合下列说法的实例？若有，请举例。
A．物体运动的加速度等于 0，而速度却不等于 0；
B．两物体相比，一个物体的速度变化量比较大，而加速度却比较小；
C．物体具有向东的加速度，而速度的方向却向西；
D．物体做直线运动，后一阶段的加速度比前一阶段小，但速度却比前一阶段大。
3．以下描述了四个不同的运动过程
A．一架超音速飞机以 500 m/s的速度在天空沿直线匀速飞行了 10 s；
B．一辆自行车以 3 m/s 的速度从某一陡坡的顶端加速冲下，经过 3 s 到达坡路底端时，速度变为 12 m/s；
C．一只蜗牛由静止开始爬行，经过 0.2 s，获得了 0.002 m/s 的速度（图 1.4–5）；
D．一列动车在离开车站加速行驶中，用了 100 s 使速度由 72 km/h 增加到 144 km/h。
（1）以上四个运动过程，哪个过程速度最大？请按速度的数值把它们由大到小排列。
（2）以上四个运动过程，哪个过程速度的变化量最大？请按速度变化量的数值把它们由大到小排列。
（3）以上四个运动过程，哪个过程加速度最大？请按加速度的数值把它们由大到小排列。
4．一个物体在水平面上向东运动，某时刻速度大小为 20 m/s，然后开始减速，2 min 后该物体的速度减小为 0。求物体的加速度大小及方向。
5．图 1.4–6 中的三条直线 a、b、c 描述了 A、B、C 三个物体的运动。先初步判断一下哪个物体的加速度最大，再根据图中的数据计算它们的加速度，并说明加速度的方向。
第 4 节 速度变化快慢的描述——加速度教学参考
1．教学目标
（1）通过抽象概括的过程，理解加速度的概念，知道加速度的定义式、方向和单位。
（2）理解加速度的矢量性，会根据速度变化的方向判断加速度的方向并结合速度的方向判断运动性质。
（3）学习并体会用物理量之比定义新物理量的方法。
（4）能用 v−t 图像分析、计算加速度，体会数学方法在物理研究中的应用及意义。
（5）理解加速度与速度、速度变化量和速度变化率之间的区别与联系，并会分析生活中的运动实例。初步体会变化率对描述变化过程的意义。
（6）通过生活中有关加速度的利用和危害防止的实例，体会物理与生活实际的紧密联系，激发物理学习兴趣。
2．教材分析与教学建议
加速度是描述物体运动的又一个重要概念。在前几节内容的基础上，加速度的引入可以更加完整、准确地描述物体的运动情况，促进学生运动观念的逐步建构。
教科书以节前“问题”引出建立加速度概念的必要性，进而启发学生仿照速度定义式得出加速度的定义式，接着进一步研究加速度矢量的方向以及如何从 v−t 图像分析加速度等问题。同时通过“思考与讨论”栏目对联系生活实际的举例，加深对加速度及相关概念的理解、辨析。
而“科学漫步”则是从更普遍的角度研究变化率的含义和意义、应用，开阔视野。“STSE”从交通工具的发展变化讨论其与社会发展、能源及环境的关系，引发学生对干人类与自然和谐发展的思考。
本节教学的重点与难点是建立和理解加速度的概念。这主要因为以下三个方面：一是加速度概念比较抽象，学生在生活经验中对它并没有清晰的印象和深入的思考，分辨不清“快”的含义是速度大还是加速度大；二是加速度矢量的方向不像速度、位移那么直观，它取决于一个对学生比较陌生的概念——速度变化量的方向，因而学生对加速度方向的理解比较困难；三是应用 v−t 图像分析加速度需要学生有一定的应用数学研究物理问题的能力。
因此教师应在教科书内容的基础上，针对难点的突破进行教学设计。可以从以下内容展开教学。
（1）问题引入
不同于前几节研究的位移、时间、速度等概念，学生对加速度既没有初中学习的概念基础，也缺乏生活中的感性认识，因此通过适当的实例引导学生思考描述速度变化快慢的方法是加速度概念建立的关键步骤。例如，教科书中就提出问题，引导学生思考如何描述小汽车和火车分别用 10 s 和 300 s 都由静止加速到 100 km/h 的运动情况。教师可以通过以下提问展开教学：
①是否能用谁的速度大描述上述过程中小汽车和火车运动的不同？
②是否能用谁的速度变化大描述上述过程中小汽车和火车运动的不同？
③你认为应该用什么方法描述它们运动的不同？
教师还可以列举相同时间间隔内速度变化不同的例子，结合上例，引导学生对问题进行思考、讨论，以感性认识促成学生对“速度”“速度变化”等概念的理解辨析及其对运动变化情况描述的不足，进而主动探索新概念——加速度（速度变化率）引入的必要性，促使学生自主建构概念。
教学片段
加速度概念的引入
让学生上网查阅汽车百公里加速时间（即汽车从静止加速到 100 km/h 的最短时间），或者汽车从 40 km/h 到停下来的制动时间。
在学生讨论的基础上，针对表 1−3 中列出的几款小汽车的百公里加速时间和 40 km/h 的制动时间（大约），组织学生讨论以下问题：
表 1−3
|
车号 |
初速度 /（km·h−1） |
末速度 /（km·h−1） |
所用时间 /s |
|
1 |
0 |
100 |
5.0 |
|
2 |
0 |
100 |
7.0 |
|
3 |
0 |
100 |
10.0 |
|
4 |
40 |
0 |
1.5 |
|
5 |
40 |
0 |
2.0 |
|
6 |
40 |
0 |
2.5 |
①1 至 3 号车加速过程的不同可以怎样描述？
②4 至 6 号车制动过程的不同可以怎样描述？
③1 号车与 5 号车的运动过程中，什么相同？什么不同？可以怎样描述？
④如果两辆汽车速度变化量和所用时间都不同，用什么物理量能描述这种不同？
⑤引入一个什么物理量就能将上述四个问题描述清楚？
引导学生分析以上问题并表达自己的观点，经过交流讨论，体会到有必要引入一个新的物理量来描述速度变化的快慢，自主生成了加速度的概念。
（2）加速度
通过实例，学生对加速度概念有了感性认识：加速度描述物体运动速度变化的快慢。在得出加速度的定义式时，教科书通过其与速度概念的类似之处——表示某个量变化的快慢，引导学生仿照速度的定义式 v = ，同样采用比值定义得出加速的定义式 a = ，并应用定义式中各物理量之间的关系得出加速度的单位为 m/s2。
这部分内容教师可以节前“问题”的讨论分析为基础，通过提示与速度定义式的类比，引导学生自主得出加速度的定义式和单位，加深对概念的理解和对比值定义物理量方法的体验。教师也可以让学生回忆初中时学过的用比值定义的物理量，如密度、压强、功率等，进一步体会物理研究方法的一致性，提升科学研究能力。
（3）加速度的方向
从加速度定义式可以看出，加速度的方向即为速度变化量的方向，因而对物理学习基础好的学生可以直接从加速度定义式及矢量运算法则分析加速度的方向。但是加速度的方向不像位移和速度的方向那么直观，而且大多数学生对矢量及其运算的理解也才开始，难以区分速度方向和速度变化量的方向，因此理解加速度的方向存在困难。所以教学中，建议将教科书上图 1.4–1 中各物理量赋值，创设实例情境。
教学片段
加速度方向与速度方向的关系
教科书图 1.41甲中汽车初速度秒 v1 = 10 m/s，末速度 v2 = 20 m/s；图乙中汽车初速度 v1 = 20 m/s，末速度 v2 = 10 m/s，两车速度变化经历的时间均为 2 s。组织学生通过定量计算和矢量作图研究讨论以下问题：
①如何用有向线段表示速度 v？
②如何计算速度变化量 Δv？Δv 是矢量吗？甲、乙两图中的 Δv 一样吗？如何用有向线段表示 Δv？
③加速度 a = ，甲、乙两图中的加速度一样吗？
④加速度是矢量吗？如何确定 a 的方向？
⑤如何定义加速运动和减速运动？
学生还没有很好地理解和掌握矢量及其运算方法，通过实例分析，加强感性认识，突破教学难点。在这里，可以类比速度的矢量性分析得出加速度的方向：根据 v = ，速度 v 的方向与位移 Δx 的方向一致，可以得出，根据加速度 a = 加速度 a 的方向与速度变化量 Δv 的方向一致。引导学生认识到：对于方向在同一条直线上的矢量运算，可似在规定正方向的前提下用正负号表示矢量的方向，这样可以把矢量运算简化为代数运算。
在加速度的概念中，包含着速度、速度变化量及速度变化快慢（速度变化率）等不同概念，初学者容易将它们混淆。应结合生活中的实例，帮助学生辨析生活中似是而非的迷思概念，加深对加速度及其相关概念的理解。为此，可以考虑设计以下问题串启发学生思考。
教学片段
a、、Δv、的关系
请举例说明以下各种情况。
①速度大，但加速度小；
②速度小，但加速度大；
③速度变化量小，但加速度大；
④加速度方向与速度方向相反；
⑤加速度方向与速度变化量方向相反；
⑥加速度大小增加而速度大小减小；
⑦加速度大小减小而速度大小增加；
⑧通过以上讨论，你能得到什么结论？
（4）从 v−t 图像看加速度
v–t 图像形象地表示了物体运动速度变化的情况，将 v–t 图像和加速度的定义式结合起来，得出图线的斜率就是速度变化率——加速度。而“科学漫步”栏目从更普遍的角度研究了“某量”“变化量”及“变化率”之间的区别与联系，突出了科学研究方法的共性，加深了对加速度的认识及对 v–t 图像的理解、应用。
学生在上一节学习了描绘物体运动的 v–t 图像，并且可以从 v–t 图像定性分析物体速度变化的情况（加速、匀速还是减速）。在此基础上，结合学生本节学习的加速度的定义式 a = ，
研究从 v–t 图像上求解加速度的方法。此处由于学生的基础和解决问题的思路不同，有的学生可能采取在 v–t 图像上找到物体做变速运动的一段时间 Δt 及相应的速度变化量 Δv，再利用加速度的定义式求出加速度；有的学生可能从数学中直线的斜率含义出发，发现加速度就是 v–t 图像的斜率，用图像斜率求加速度。教学中应鼓励学生自主探索、交流问题的解决方案，增强应用数学知识分析物理问题的意识和能力。
需要说明的是，教科书中提出了 v–t 图像斜率的概念，明确指出 v–t 图像斜率的物理意义——加速度。这进一步将物理规律与数学方法有机结合起来，同时又为以后其他图像斜率含义的研究打下基础。教学中应注重用图像研究物理问题的能力培养。
这一部分教学可以组织学生以小组为单位分析 v–t 图像，讨论 v–t 图像的含义以及如何从 v–t 图像求解加速度。不同的学生选取的方法可能不同，这样可以使讨论的结果更具有普适性。讨论的过程可参考下例。
教学片段
从 v−t 图像看加速度
针对教科书图 1.4–2 中的 v–t 图像（可视学生情况在图上补充一个匀减速运动的图线），可以组织学生讨论以下问题：
①学生分组讨论 v–t 图像的含义。例如，可以讨论如何知道物体某一时刻的速度、一段时间内的速度变化量及速度变化率等。
②确定本组根据 v–t 图像分析加速度的方法并求出加速度。
|
图 1−9 |
③各组交流方法和结果。特别要引导学生分析针对同一 v–t 图像，不同组选取的 Δt 和 Δv 不同，为什么求出的加速度相同？这反映出 v–t 图像的什么特点？
④分析每个 v–t 图像的倾斜程度（包括走向）与对应求得的加速度大小及方向（指正负号）之间的关系。
⑤总结得出 v–t 图像斜率的含义及由 v–t 图像求加速度的方法。
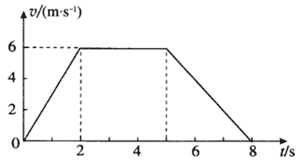
⑥讨论乘电梯上楼的速度变化情况，画出 v–t 图像的草图。
⑦如将乘电梯上楼的速度变化简化成如图 1–9 表示的情境，试分析各阶段物体的运动情况，求出相应的加速度。
|
图 1−10 |
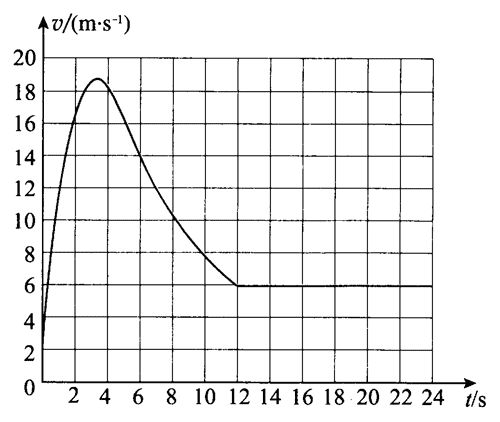
对学有余力的学生可以让其分析如图 1–10 中跳伞运动员下落过程的 v–t 图像，体会加速度发生变化的运动情况。然后启发学生仿照平均速度和瞬时速度的定义，提出平均加速度和瞬时加速度的定义。并引导学生进一步研究如何从 v–t 图像上求出平均加速度和瞬时加速度。
“STSE”从交通工具的发展变化，到城市的发展、战争的变化、国际经济与贸易的发展以及交通发展带来的环境和社会的问题。此处可以组织学生学习和查阅相关资料并交流讨论，引发学生对于人类与自然和谐发展的思考，促进科学态度与责任的培养。
3．“练习与应用”参考答案与提示
本节课配备 5 道习题，要求学生较好地理解加速度的定义式，以及速度、速度变化量与加速度之间的关系。第 1 题考查实际情境中的加速度计算，通过汽车的加速性能——“百公里加速时间”理解加速度的概念，并计算三种轿车的加速度值，尝试用所学的加速度知识解决一些日常生活中遇到的问题，培养学生学习和研究物理的好奇心和求知欲。第 2 题需要学生按要求举例，从中体会速庋、速度变化量与加速度之间的关系。第 3 题给出具体情境，要求学生比较速度、速度变化量及加速度的大小。第 4 题重在帮助学生认识加速度的矢量性在一维运动中的表示方法。第5题在 v-t 图像中比较加速度的大小，计算加速度。
1．2.46 m/s2；2.11 m/s2；1.79 m/s2
提示：由 v = 100 km/h = 27.8 m/s 可知，aA = = = 2.46 m/s2，aB = = = 2.11 m/s2，aC = = = 1.79 m/s2。
2．A．汽车做匀速直线运动时加速度等于 0，速度不等于 0。
B．根据本节教科书中提供的素材可以估算：高铁从静止加速到 100 km/h 大约需要 80 s，赛车从静止加速到 72 km/h 大约需要 4.5 s。高铁的速度变化量比赛车的大，而加速度却比赛车的小。
C．物体向西做减速运动时，速度方向向西，但加速度向东。
D．汽车加速到最大速度的过程中，汽车会做加速度减小的加速运动，速度增大，加速度减小。
3．（1）飞机的速度最大；速度值由大到小的排序为：飞机、动车、自行车、蜗牛。
（2）飞机在 10 s 内的速度变化量为 0，自行车在 3 s 内的速度变化量为 9 m/s，蜗牛在 0.2 s 内的速度变化量为 0.002 m/s，动车在 100 s 内的速度变化量为 72 km/h = 20 m/s。可见，动车的速度变化量最大；速度变化量的数值由大到小的排序为：动车、自行车、蜗牛、飞机。
（3）飞机的加速度为 0，自行车的加速度为 3 m/s2，蜗牛的加速度为 0.01 m/s2，动车的加速度为 0.2 m/s2。可见，自行车的加速度最大；加速度的数值由大到小的排序为：自行车、动车、蜗牛、飞机。
4．0.17 m/s2，方向水平向西
提示：a = = = − 0.17 m/s2，式中负号表示加速度方向水平向西。
5．A 的斜率最大，加速度最大。aA = 0.63 m/s2，aB = 0.08 m/s2，aC = − 0.25 m/s2，物体 A、B 的加速度方向与速度方向相同，物体 C 的加速度方向与速度方向相反。
参考解答：2.46 m/s2；2.11 m/s2；1.79 m/s2
参考解答：A．汽车做匀速直线运动时加速度等于 0，速度不等于 0。
B．根据本节教科书中提供的素材可以估算：高铁从静止加速到 100 km/h 大约需要 80 s，赛车从静止加速到 72 km/h 大约需要 4.5 s。高铁的速度变化量比赛车的大，而加速度却比赛车的小。
C．物体向西做减速运动时，速度方向向西，但加速度向东。
D．汽车加速到最大速度的过程中，汽车会做加速度减小的加速运动，速度增大，加速度减小。
参考解答：（1）飞机的速度最大；速度值由大到小的排序为：飞机、动车、自行车、蜗牛。
（2）飞机在10 s内的速度变化量为0，自行车在 3 s 内的速度变化量为 9 m/s，蜗牛在 0.2 s 内的速度变化量为 0.002 m/s，动车在 100 s 内的速度变化量为 72 km/h = 20 m/s。可见，动车的速度变化量最大；速度变化量的数值由大到小的排序为：动车、自行车、蜗牛、飞机。
（3）飞机的加速度为 0，自行车的加速度为 3 m/s2，蜗牛的加速度为 0.01 m/s2，动车的加速度为 0.2 m/s2。可见，自行车的加速度最大；加速度的数值由大到小的排序为：自行车、动车、蜗牛、飞机。
参考解答：0.17 m/s2，方向水平向西
参考解答：A 的斜率最大，加速度最大。aA = 0.63 m/s2，aB = 0.08 m/s2，aC = − 0.25 m/s2，物体 A、B 的加速度方向与速度方向相同，物体 C 的加速度方向与速度方向相反。
发布时间：2019/9/21 下午10:00:10 阅读次数：30135
