1．迈克尔逊干涉仪是光学干涉仪中最常见的一种，发明者是美国物理学家阿尔伯特·亚伯拉罕·迈克尔逊。最初设计迈克尔逊干涉仪的目的是为测量“以太”（假想的传播光的媒质）的漂移速度，目前它广泛应用于精密测量。迈克尔逊干涉仪的光路图如图 1a 所示：

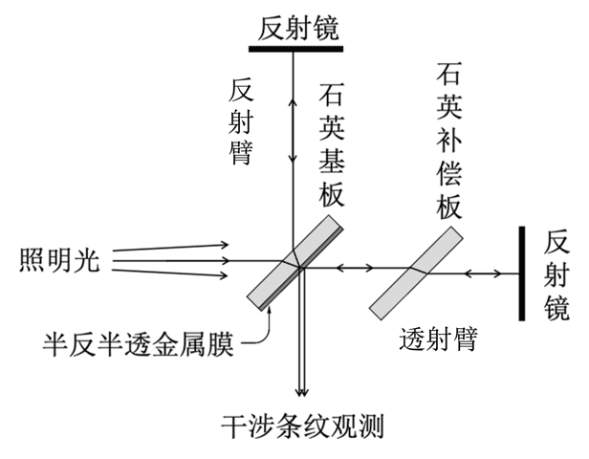
照明光为单色激光，入射光经过半反半透的镜子分为沿干涉仪的两个臂（反射臂和透射臂）传播的两束光。半反半透镜与入射光轴方向之间的夹角为 45°，反射臂和透射臂相互垂直。在两个臂端上各放置与相应的臂垂直的反射镜，反射镜可以沿臂的方向移动。反射和透射光线经反射镜反射，再次经过半反半透镜透射和反射，两束光在空间重叠，发生干涉。如果照明光为发散光源，我们观察到的干涉条纹为同心圆环。半反半透镜是在一个平整的石英基板上蒸镀一层薄金属膜制成，迈克尔逊干涉仪中参与叠加的两束光都经过半反半透镜的反射，一束光是在石英和金属界面上的反射，另一束光是在空气和金属界面上的反射。因为反射界面不同，所以两束光反射时相位突变不同，两者的差异为 Δφ，下面我们通过实验测量 Δφ。开始时，观察到干涉场中心是亮斑，干涉场最外侧是亮圆环，一共 20 个亮条纹（计及中心亮斑）。现在缓慢调节一个臂的反射镜，让反射镜沿臂的方向平移，观察到干涉条纹发生明暗变化，并发现同心圆环条纹越来越稀疏。干涉场中心明暗变化了 23 个周期，干涉场最外侧的明暗变化了 20 个周期。（本题中，条纹数目均视为精确计数值，干涉仪两臂的长度在 cm 量级。）

（1）求相位突变差异 Δφ。

（2）反射镜移动后，可以观察到多少个干涉亮条纹（计及中心亮斑）？

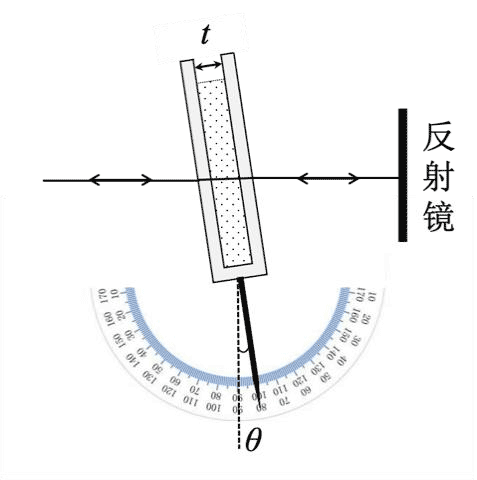
（3）使用此干涉仪测量某一透明液体的折射率，将扁平的石英空槽插入迈克尔逊干涉仪的一个臂，使得石英槽的表面与臂的方向垂直。然后调节石英槽与臂之间的夹角，使之改变 θ = 5.00°；在角度改变过程中，干涉场中心明暗变化了 10 个周期。现将待测液体注入石英槽，如图 1b 所示。再次调节石英槽的倾斜角度，使其恢复到与臂垂直，在此过程中，干涉场中心明暗变化了 17 个周期。已知照明光波长为 633 nm ，石英槽内壁间距为 t = 2.00 mm，空气的折射率为 1.00。求待测液体的折射率。

【答案】

第39届全国复赛1

 

2．某长直弹簧由涂了绝缘漆的磷铜细丝绕制 N 匝而成，可视为横截面半径为 r 的长直螺线管。弹簧原长为 l₀（l₀ ≫ r），劲度系数为 k。假设在弹簧形变过程中，螺线管始终可视为均匀密绕的，其横截面半径的变化可忽略。不计边缘效应、漏磁和重力。真空磁导率为 μ₀。

（1）用恒流源通过柔软导线对螺线管通以不变的电流 I₀，通电期间用外力使弹簧处处无形变。缓慢撤除外力后，弹簧达到新的平衡位置（但仍可压缩或拉伸），此时的长度记为 l_p。

（i）试导出可求解 l_p 的代数方程（但不必求解），并求通电弹簧在其平衡位置附近发生小幅度形变时的等效弹性系数 k_eff（表达式中可以含有参量 l_p）；

（ii）求能实现上述平衡状态的 I₀ 的取值范围（表达式中不得含有参量 l_p）。

（2）改变（1）问中的通电条件，如果弹簧螺线管两端先用电阻为零的柔软理想导线连接形成回路，并假设弹簧螺线管电阻也为零，且在初始时回路已加载电流 I₀ʹ，并用外力使弹簧处处无形变。缓慢撤除外力后，弹簧达到新的平衡位置（但仍可压缩或拉伸），此时的长度记为 l_pʹ。试求 l_pʹ、以及通电弹簧在其平衡位置附近发生小幅度形变时的等效弹性系数 kʹ_eff。

【答案】

第39届全国复赛2

 

3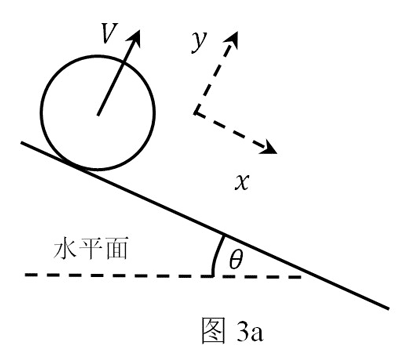．如图 3a，将质量为 m、半径为 R 的匀质实心球从倾角为 θ 的无限长固定斜面上发射，已知球心初速度垂直于斜面，大小为 V，球初始的自转角速度为零。为方便描述实心球此后的运动，在斜面参考系中建立如图 3a 所示的平面直角坐标系，其中 x 轴沿斜面向下，y 轴垂直于斜面向上。假设球与斜面的碰撞是弹性的，碰撞时间极短，且碰撞前、后的瞬间球垂直于斜面的速度大小不变。进一步假设斜面足够粗糙，以至于在球与斜面的碰撞过程中，其间摩擦力足够大、接触点无相对滑动。已知球绕其直径的转动惯量为 I = \(\frac{2}{5}\)mR²，求

（1）第 1 次碰撞前的球心速度和球的自转角速度；

（2）第 1 次碰撞后的球心速度和球的自转角速度；

（3）第 n 次碰撞后球心沿着 x 轴方向的速度以及球的自转角速度；

（4）前 n 次碰撞过程中斜面对球施加的总冲量。

【答案】

第39届全国复赛3

 

4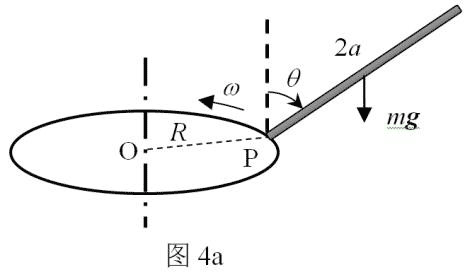．如图 4a，一根长度为 2a、质量为 m 的匀质刚性细杆，其一端有一小孔，嵌套在半径为 R 的水平圆环的 P 点处（ P 是圆环上的固定点）；P 点（连同杆）随圆环一起绕圆环中心轴以恒定角速度 ω 转动；同时，杆可绕 P 点无摩擦地转动，且杆和圆环矢径 OP 始终在同一竖直平面内；杆与竖直方向之间夹角为 θ。重力加速度大小为 g。

（1）将所有类型的保守力做功都与势能变化相联系，试分别在实验室系 L 和在随矢径 OP 转动的转动参考系S 中，写出杆的机械能表达式（表达式中可以含有 θ ）；

（2）在 S 参考系中导出杆处于平衡位形时，θ 所需满足的条件；

（3）在 S 参考系中，对于第（2）问中得到的结果，利用图解法分析 θ 取值在 Ⅰ （0 ≤ θ ≤ π/2）、Ⅱ（π/2 ≤ θ ≤ π）、Ⅲ（π ≤ θ ≤ 3π/2）、Ⅳ（3π/2 ≤ θ ≤ 2π）象限中，分别可能出现的杆的平衡位形的数目，以及相应的 a、R、ω 各参量之间需要满足的条件；

（4）在 S 参考系中，分象限画出对杆所受到的相对于 P 点的力矩有贡献的受力示意图（对于分布性的力，仅需示意性地画出其对 P 点力矩有贡献的等效合力），查看是否可能出现平衡位形，以检验（3）中分析的结果；

（5）试讨论（3）中所确定的杆的各个平衡位形的稳定性。

【答案】

第39届全国复赛4

 

5．两根相同的理想轻弹簧，劲度系数均为 k、自然长度均为 0。两弹簧之间以一质量为 m 的小球相连。将弹簧 1 空着的一端悬挂于天花板上，整个系统自然下垂，初始时静止。已知两弹簧中任意一个一旦被拉伸至临界长度（该临界长度大于 \(\frac{{mg}}{k}\)，这里 g 表示重力加速度的大小）便会被拉断。

实验发现，如果缓慢地拉动下面的弹簧 2 的下端，上面的弹簧 1 将被拉断。如果快速地拉动，则很有可能拉断下面的弹簧 2。

（1）设加载于弹簧 2 下端的作用力随时间变化的关系为 F(t)，写出弹簧 1 的长度 x₁(t) 及小球加速度 \({{\ddot x}_1}(t)\) 所满足的运动方程。

（2）在一个简单模型中，假设 F(t) 与时间 t 的关系为

\[F(t) = \left\{ {\begin{array}{*{20}{c}}{0\;\;t < 0}\\{\alpha t\;\;t \ge 0}\end{array}} \right.\]

其中 α 为大于零的常量，它的大小对应力加载的快慢。求在该力的作用下弹簧 1、2 在 t （t > 0）时刻的长度 x₁(t)、x₂(t)。

（3）记某一弹簧先被拉断的时刻为 t₀，根据（2）中的结果，

（i）求使弹簧 1 必然先被拉断所对应的 α 取值范围；

（ii）对于并非必然使弹簧 1 先被拉断的 α 取值，分析使弹簧 1 先被拉断的时刻 t₀ 需满足的条件（表达式中可含有 α）；

（iii）求弹簧 2 先被拉断的可能性与 α 取值大小的关系，并用此关系说明题述实验现象。

（4）给定临界长度为 L，要确保弹簧 2 先被拉断，试确定 α 需满足的关系式。有无可能两弹簧同时被拉断？若有，试求出能让两弹簧同时达到临界长度 L 所对应的 α 满足的关系式。

【答案】

第39届全国复赛5

 

6．金属内部有温度梯度时可以在其两端产生电动势，该效应被应用于热电偶温度计等。为了分析此现象，现建立一个简单的经典玩具模型，如图 6a 所示：一厚度为 2L、沿着 y、z 方向无限延展的金属平板，位于 – L < x < L 区域；而 | x | > L 区域为真空，电场为零。将金属内的导电电子视为在空间均匀的正电荷背景上运动的经典理想气体。没有温度梯度时，呈电中性的金属内部的电子是完全均匀分布的，其数密度为 n₀；有温度梯度时，金属内的温度是 x 的函数，T(x) = T₀ + δT(x)，且 | δT(x) | ≪ T₀。在（局域）热平衡状态下，金属内电子数密度 n(x) = n₀ + δn(x) 会略微偏离 n₀，| δn(x) | ≪ n₀。金属内部也会有很小的沿 x 方向的电场 E_x(x)。金属表面 x = ±L 内侧也分别有很小的面电荷密度 σ ₊ 和 σ ₋。已知电子质量为 m，所带电荷为 − e（e > 0）。忽略重力，玻尔兹曼常量为 k_B。

（1）粒子数密度 n(x) 的不均匀性会引起粒子的扩散。若在时间间隔 dt 内通过 yz 平面上面积为 dA 的粒子数为j_xdAdt，则 j_x 被称为粒子流密度。粒子扩散流密度 j_x(x) 满足斐克（Fick）定律

J_x(x) = − D \(\frac{{\rm{d}}}{{{\rm{d}}x}}n(x)\)

式中 D 是扩散系数

D = c \(\frac{{\sqrt {T(x)} }}{{n(x)}}\)

这里，c 是已知常量。在平衡状态下，金属内部应该没有净的电流，因此前述的电子扩散流会被内部电场产生的漂移电流抵消。为简化起见，设金属的电阻率 ρ 是与 n(x)、T(x) 等无关的已知常量。求金属板内部电场 E_x(x) 的表达式（用 n(x)、T(x)、\(\frac{{\rm{d}}}{{{\rm{d}}x}}n(x)\) 和其他常量表出）。

（2）试由静电场高斯定理导出 E_x(x) 满足的微分方程；并利用（1）的结果消去电场 E_x(x)，导出 n(x) 满足的微分方程和边界条件。真空介电常量为 ε₀。（提示：净的电荷密度包含正电荷背景）

（3）将（2）中方程线性化，即只保留 δn、δT 等小量的线性项，解出 δn(x)（解中可包含 σ ₊ 和 σ ₋）。

（4）假设金属内存在温度梯度，即 δT(x) 不为零，但在任意 x 处电子气（可视为理想气体）处于局域热平衡；电子气中的电子受到电场 E_x(x) 的作用，但厚度为 dx 的薄层内的电子气仍处于宏观的力学平衡状态。试导出 δT(x) 满足的微分方程，并将其线性化。再利用（3）的结果，求出 δT(x)。

（5）根据（3）和（4）的结果，求出金属两端（x = − L 和 x = + L）的电势差和温度差的比值（即金属的 Seebeck 系数 S）

S = \(\frac{{U(L) - U( - L)}}{{T(L) - T( - L)}}\)

附注：对金属温差电现象的正确分析必须考虑电子的量子效应，本题目中的简化经典模型并不适用于真实情况。

【答案】

第39届全国复赛6

 

7．欧洲核子研究中心的大型强子对撞机上进行了高能铅核-铅核碰撞的实验，碰撞后的初始产物可视为温度很高的“火球”，其内的物质主要由静止质量很小、速度极其接近于光速的夸克组成。本题忽略该物质中除夸克外的其他组分，将其视为“夸克物质”，并将夸克都近似视为质点，夸克之间除相互碰撞的瞬间外无相互作用，碰撞过程中粒子数目守恒，其速度分布是各向同性的。已知温度为 T 时，在任一动量大小区间 [p,p + dp] 内，夸克物质中能量为 E 的夸克粒子的分布比率（概率分布密度）正比于 \({e^{\frac{E}{{{k_{\rm{B}}}t}}}}\) 4πp²dp，其中玻尔兹曼常量 k_B 或理想气体普适常量 R 视为已知量。

（1）试在本题模型近似下，导出夸克物质的状态方程（用压强 P 与能量密度平均值 u 之间的关系表出）。

（2）试在本题模型近似下，导出夸克物质以压强 P、粒子数密度 n 和温度 T 之间的关系表述的状态方程。

（3）试在本题模型近似下，求夸克物质的定体摩尔热容 C_V 和热容比 γ（定压摩尔热容与定体摩尔热容的比值）。

（4）假设铅核-铅核碰撞的早期产物形成的“火球”近似为球形，半径约为 3.0 × 10⁻¹⁵ m，其中的夸克物质温度约为 400 MeV/k_B。此后，“火球”迅速膨胀降温，至温度约为 150 MeV/k_B 时，夸克物质中的夸克开始被束缚在一起形成质子和中子。假设“火球”的膨胀降温过程可近似为准静态的绝热过程，求出质子和中子刚刚形成时“火球”的半径。

【答案】

第39届全国复赛7