1．物体做曲线运动过程中一定发生变化的是

（A）速度大小            （B）速度方向            （C）加速度大小        （D）加速度方向

【答案】

B

 

2．一列火车持续鸣笛并快速经过火车站，在火车头经过站在站台上的某同学的前后一段时间内，该同学听到汽笛声的频率

（A）逐渐升高                   （B）逐渐降低

（C）先升高后降低            （D）先降低后升高

【答案】

C

 

3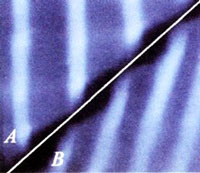．如图所示，一列水波在两种不同深度水体 A、B 的分界面上同时发生了反射和折射，其中反射波与折射波的

（A）波长相同                          （B）波速大小相同

（C）周期相同                          （D）传播方向相同

【答案】

C

 

4．下列过程中，机械能近似守恒的是

（A）电梯匀速下降                   （B）跳水运动员入水至最低点

（C）橡皮从桌上掉落               （D）木箱在拉力作用下沿地面匀速前行

【答案】

C

 

5．如图所示为停在海面上的轮船的卫星照片，图中的海水波纹

（A）只反映波的干涉        （B）同时反映波的干涉和衍射

（C）只反映波的衍射        （D）既不反映干涉，也不反映衍射

【答案】

B

 

6．地球半径为 r₁，赤道上某点随地球自转的线速度大小为 v₁，某轨道半径为 r₂ 的地球同步卫星运动的线速度大小为 v₂，则 \(\frac{{{v_1}}}{{{v_2}}}\) 为

（A）\(\frac{{{r_1}}}{{{r_2}}}\)           （B）\(\frac{{{r_2}}}{{{r_1}}}\)        （C）\(\frac{{r_1^2}}{{r_2^2}}\)             （D）\(\frac{{r_2^2}}{{r_1^2}}\) 

【答案】

A

 

7．我国首次火星探测任务被命名为“天问一号”。已知火星质量约为地球质量的 10%，半径约为地球半径的 50%，则

（A）火星探测器的发射速度应大于地球的第二宇宙速度

（B）火星探测器的发射速度应介于地球的第一和第二宇宙速度之间

（C）火星的第一宇宙速度大于地球的第一宇宙速度

（D）火星表面的重力加速度大于地球表面的重力加速度

【答案】

A

 

8．将固有频率分别为 f_I、f_II 的 I、II 两振子固定在同一振台上，打开振台后逐渐调大振台的驱动力频率。已知 f_I < f_II，则关于两振子受迫振动的振幅 A_I、A_II

（A）不可能 A_I、A_II 同时增大         （B）不可能在 A_I 增大的同时 A_II 减小

（C）不可能 A_I、A_II 同时减小         （D）不可能在 A_I 减小的同时 A_II 增大

【答案】

B

 

9．一根粗细均匀的绳子，右端固定，一人拿着左端的 O 点上下振动。以竖直向上为正方向，波源 O 在第一个周期内的振动图像如右图所示，则该波在第一个周期结束时在介质中形成的波形图是

【答案】

D

 

10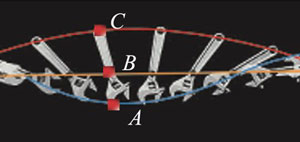．右图为光滑水平面上一扳手在甩出后旋转着向右运动的部分频闪照片，某时刻扳手上 A、B、C 三点位置标注如图，该时刻三点的速度大小分别为 v_A、v_B、v_C，加速度大小分别为 a_A、a_B、a_C，则

（A）v_C > v_B > v_A，a_A = a_C > a_B

（B）v_C > v_B > v_A，a_C > a_A > a_B

（C）v_C > v_B > v_A，a_A = a_B = a_C

（D）v_A = v_B = v_C，a_A = a_B = a_C

【答案】

B

 

11．一杯水搅动后形成如图所示上大下小的“喇叭”形漩涡。漂浮在漩涡内壁水面上的 a、b 两轻小物体随水流在水平面内做匀速圆周运动，加速度大小为 a_a、a_b，角速度大小为 ω_a、ω_b，则

（A）a_a > a_b，ω_a > ω_b                （B）a_a > a_b，ω_a < ω_b

（C）a_a < a_b，ω_a > ω_b                 （D）a_a < a_b，ω_a < ω_b

【答案】

A

 

12．类比直线运动中用 v-t 图像求位移的方法，关于图像与横坐标轴围成面积的意义

（A） 若图像为 x-t（位移-时间）图，面积反映速度大小

（B）若图像为 a-t（加速度-时间）图，面积反映位移大小

（C）若图像为 F-x（力-位移）图，面积反映力的功率

（D）若图像为 P-t（功率-时间）图，面积反映力做的功

【答案】

D

 

13．如图，一轻弹簧的左端固定在墙壁上，右端连接一个小球，小球放置在光滑水平地面上。弹簧处于原长时，小球在位置 O。将小球拉至位置 A 后由静止释放。释放后，小球从 A 第一次运动到 O 的过程中，小球的加速度

（A）保持不变           （B）逐渐减小            （C）逐渐增大            （D）先增大后减小

【答案】

B

 

14．如图，一轻弹簧的左端固定在墙壁上，右端连接一个小球，小球放置在光滑水平地面上。弹簧处于原长时，小球在位置 O。将小球拉至位置 A 后由静止释放。释放后，小球从 A 第一次运动到 O 的过程中，弹簧的弹性势能

（A）保持不变           （B）逐渐减小            （C）逐渐增大            （D）先增大后减小

【答案】

B

 

15．如图，一轻弹簧的左端固定在墙壁上，右端连接一个小球，小球放置在光滑水平地面上。弹簧处于原长时，小球在位置 O。将小球拉至位置 A 后由静止释放。释放后，小球从 A 第一次运动到 O 的过程中，小球与弹簧所组成系统的机械能

（A）保持不变           （B）逐渐减小            （C）逐渐增大            （D）先增大后减小

【答案】

A

 

16．如图，一轻弹簧的左端固定在墙壁上，右端连接一个小球，小球放置在光滑水平地面上。弹簧处于原长时，小球在位置 O。将小球拉至位置 A 后由静止释放。释放后，小球从 A 第一次运动到 O 的过程中，下列各示意图中正确反映小球速度 v 随时间 t 变化关系的是

【答案】

A

 

17．开普勒第三定律 r³/T² = k，比值 k 的单位可用国际单位制中的基本单位表示为________；若已知太阳质量为 M，地球公转轨道半径为 r，万有引力常量为 G，则该比值 k 可表示为___________。

【答案】

m³/s²，GM/4π²

 

18．某质点从 A 点沿图中的曲线运动到 B 点，质点受力的大小为 F。经过 B 点后，若力的方向突然变为与原来相反，它从 B 点开始可能沿图中虚线_______运动，请简述理由（可结合图示）：_____________________________。

【答案】

a，质点由 A 点运动到 B 点，F 方向为指向曲线弯折方向，在 B 点，速度方向为过 B 点的切线方向；经过 B 点后，F 方向相反，轨迹应在此时的 F 方向和速度方向之间。

 

19．如图甲所示为一皮带传动装置，a、b、c 点在各自轮边缘，其圆周运动对应的半径分别为 r、2r 和 4r，若传动过程中皮带不打滑，则 a、b、c 三点的周期之比 T_a∶T_b∶T_c = _______。如图乙为描述向心加速度 a_n 与半径 R 之间的关系的 a_n-R 图像，其中 ① 为反比例图线、② 为正比例图线，试在图乙中标出可代表 a、b、c 三点 a_n-R 关系的数据点。

  

【答案】

1∶2∶2，如图

 

20．如图，一小球 A 从某高处由静止开始下落，选择不同平面为参考平面，下落过程中小球具有的能量及其变化情况如下表所示，请在表格中将未填写的数据补充完整。

所选择的参考平面	下落初始时刻的机械能 E1	下落到地面时的机械能 E	下落到地面时的重力势能 Ep	下落过程中重力势能变化量 ∆Ep	下落到地面时的动能 Ek
四楼地面		− 2.5 J			9 J
一楼地面	9 J		0

【答案】

−2.5 J，− 11.5 J，9 J，− 9 J

 

21．科学探究情境：

游乐场的“海盗船”（如图）是同学们非常喜欢的游乐项目，启动时海盗船在电机作用下来回摆动，结束过程中电机关闭，海盗船渐渐停下来。小明同学在体验了这一项目后，决定和同学合作运用物理课所学进行探究。

请与他们一起完成如下探究问题。

问题一：

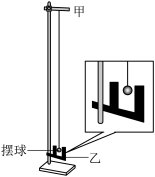
要将“海盗船”搬到实验室，小明组内讨论首先要进行简化处理。他们选用了小钢球、细绳、铁架台，搭建了如图 a 所示的“摆”结构。你认为他们这样简化所采用的物理思想方法是_____________。

问题二：

小组认为：海盗船项目存在一定的风险，尤其是当其摆到最低点位置，他们认为此处连接船体的连接杆的力 F 最大，并猜想该力 F 与海盗船摆到最低点时的速度 v 有关。于是，他们在“摆”结构上进行探究：

（1）首先，小组在铁架台甲处固定了力传感器用以测量细绳上的拉力 F，并在最低点乙处安装了_____传感器用以测量钢球速度，如图 b 所示。

（2）接着，他们测出小钢球半径 r 和细线的长度为 L。将小球拉到某一位置释放，若测量出小球到达最低点的速度为 v、小球质量为 m，重力加速度为 g，则理论上小球到最低点时，力 F 的表达式为__________；

（3）然后，小组分别将小球从不同位置释放，测出每次小球在最低位置时的 F 和 v，如下表：

位置	1	2	3	4	5
F/N	0.56	0.60	0.64	0.70	0.90
v/（m/s）	0.40	0.50	0.60	0.70	1.00

对表中数据进行处理后，将数据点拟合，得到图 c，则图像中水平轴应为_____（填写物理量符号）；取重力加速度 g = 10 m/s²，根据图像可推测小球的质量 m 约为______kg，用天平进行了证实，发现质量有较小的差别。

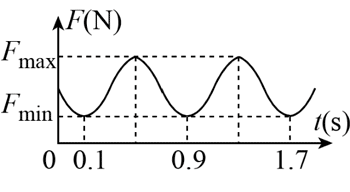
（4）接着，小明认为质量“有较小的差别”是因为重力加速度 g 取值与实际值略有偏差，于是他们将摆球摆动的角度控制在 5° 范围内，再次用传感器测出细线拉力 F 随时间 t 的变化图像，如图 d，测出此时细线长为 63 cm、小钢球直径为 1.0 cm，则重力加速度应该修正为 g = __________m/s²；

（5）最后，小组经过讨论认为每次将小钢球以不同的初速度释放，图 c 的数据图像的形态和位置____________（选填“会”或“不会”）改变。

问题三：

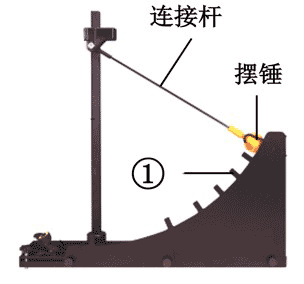为了探究海盗船运行过程中的能量情况，小组又采用了如图所示的“验证机械能守恒定律”的实验装置。

（1）该实验装置中 ① 为_______；数据处理时，连接杆的动能和重力势能可以忽略不计，这是由于：______________；

（2）若将连接杆放置在图示位置由静止释放，已知连接杆悬点到摆锤质心的距离为 l，杆与竖直方向夹角为 θ，不计阻力，则摆锤运动到最低点的速度应为多大？（请写出分析过程）

（3）增大摆锤的迎风面，将质量为 m 的摆锤仍于图示位置由静止释放，测得最低处速度为 v，则可推得此过程中阻力对摆锤做功为______________。

【答案】

问题 1：

物理模型（模型建构）

问题 2：

（1）光电门

（2）mg + mv²/(L+r)

（3）v² （2 分），0.05

（4）9.79（9.78 ~ 9.79 均给分）

（5）不会

问题 3：

（1）挡光片，连接杆质量远小于摆锤质量

（2）下摆过程中，由动能定理  ΣW = W_G = ΔE_k

mgh = \(\frac{1}{2}\)mv² – 0，其中，h = l – lcosθ

可得       v = \(\sqrt {2gl(1 - \cos \theta )} \)

（3）\(\frac{1}{2}\)mv² – mgl(1 – cosθ)

 

22．有同学设计了一个估测如图甲所示吹风机出风口最强挡气流速度的简易实验。图乙是实验的原理示意图，轻质挡板放在摩擦可以忽略的平台上，连接挡板的轻质弹簧固定在右壁上，所用精密弹簧的劲度系数 k = 39.6 N/m。该同学测量了吹风机圆形出风口的横截面积为 S = 2.20×10⁻³ m²。吹风机内加热后的空气密度 ρ = 1.26 kg/m³。

（1）起初挡板左边缘静止在 x₁ = 1.50 cm 处，当开启吹风机正对着挡板吹风时，挡板左边缘处的刻度如图乙所示的 x₂ = 2.20 cm 处，求此处的弹簧对挡板的弹力大小；

（2）若吹风机吹出空气风速为恒为 v = 5 m/s，求每秒吹风机吹出的空气动能；

（3）该同学利用所学，推导出了风速 v 的一般表达式为 v = \(\sqrt {\frac{{k({x_2} - {x_1})}}{{\rho S}}} \)（x₁ 和 x₂ 为挡板两处位置刻度值），请根据国际单位制论述此表达式是否正确？并用物理量的代表字母推导出该表达式。

【答案】

（1）F = 0.28 N

（2） \(\frac{1}{2}\)ρSv³

（3）正确

对于 ∆t 时间内撞上挡板的空气柱，在弹力 F 作用下，速度从 v 减速到零

由牛顿第二定律 F = ma

k(x₂ – x₁) = ρSvΔt·\(\left( {\frac{{0 - \Delta v}}{{\Delta t}}} \right)\) = ρSv²

v = \(\sqrt {\frac{{k({x_2} - {x_1})}}{{\rho S}}} \)

 

22．如图甲所示，一小物体在拉力 F 作用下由静止开始沿足够长的光滑斜面向上运动，拉力 F 平行斜面，已知拉力 F 及小物体速度 v 随时间 t 变化的规律如图乙所示。重力加速度 g 取 10 m/s²，试求：

（1）物体在 1 s 末的加速度大小；

（2）物体的质量 m 及斜面倾角 𝜃；

（3）前 4 s 内，物体的机械能变化；

（4）简述前 4 s 内的做功与能量转化关系。

【答案】

（1）a = 0.5 m/s²

（2）m = 1 kg，θ = 30°

（3）ΔE = 15.5 J

（3）前 4 s 内，通过拉力 F 做功 15.5 J，消耗外界能量转化为物体的机械能，其中，15 J 通过克服重力做功转化为物体重力势能，0.5 J 通过拉力与重力所做的总功转化为物体的动能