电磁波的传播互动课件

这个程序要实现的是沪科版选择性必修二第八章 第三节 电磁波的传播和接收中的图 8–12。如下图所示。

做出的成品如下所示：

核心代码解读

波的绘制

物理涉及到的知识（虽然高中不教）是机械波的函数方程（即波函数），它描述了波在空间和时间上的振动状态。对于最常见的沿 x 轴正方向传播的一维简谐行波的波函数的基本形式如下：

\[y(x,t) = A\sin (kx - \omega t + {\varphi _0})\]

式中：

• y(x,t)：t 时刻时、x 位置处的质点的振动位移（相对于平衡位置）。
• A：振幅。
• k：波数（k = \(\dfrac{{2\pi }}{\lambda }\)，λ 为波长）。
• ω：角频率（ω = 2πf = \(\dfrac{{2\pi }}{T}\)，f 为频率，T 为周期）。
• φ₀：初相位（由初始条件决定）。
• kx – ωt + φ₀：相位，决定质点在特定时空点的运动状态。

上述函数也可以用波速表示：

\[y(x,t) = A\sin \left[ {\frac{{2\pi }}{\lambda }(x - vt) + {\varphi _0}} \right]\]

程序中使用的就是上面的表达式。课件在 900 px 范围内绘制一列行波，波速 900 px/s 保持不变，对应现实中光速 c = 3×10⁸ m/s 保持不变。频率范围 1 ~ 3 个单位，只能以 0.5 的步进改变数值；根据 λ = \(\dfrac{v}{f}\)，拖动频率滑动条时，可在900 px的范围内绘制 1、1.5、2、2.5、3 个波形。每列波使用了 200 个采样点，将这些点用直线连接起来就形成了一列简谐波。

以在 900 px 中画一个波形为例，即波长 λ = 900 px，f = 1 Hz，则 ω = 2π，第 1 个采样点以遵循 y₁ = Asint 的规律上下振动，第 2 个采样点振动频率相同，但相距第 1 个采样点 900/200 = 4.5 px，在时间上推迟落后 \(\dfrac{4.5}{900}\) = \(\dfrac{1}{200}\) s 开始振动，即相位上落后 \(\dfrac{4.5}{900}\)×2π，后面的点依此类推。代码实现如下：

// 生成XY平面的正弦波点（z=0）- X轴向右延伸（使用正x值）
for (let i = 0; i <= segments; i++) {
  const x = i * totalLength / segments; // x从0到900像素（向右延伸）
  // 添加随时间变化的相位偏移，实现波的传播动画
  const y = params.amplitude * Math.sin(2 * Math.PI / waveLength * (x - v * params.time));
  const z = 0; // XY平面

  // 将3D点投影到2D
  const projected = project3DTo2D(x, y, z, params);
  points.push(projected);
}

// 生成SVG路径，添加填充效果
const path = document.getElementById('sineWaveXY');
if (points.length > 0) {
  let pathData = `M ${points[0].x},${points[0].y}`;
  for (let i = 1; i < points.length; i++) {
    pathData += ` L ${points[i].x},${points[i].y}`;
  }
  // 添加返回起点的路径，形成闭合区域
  const startXZ = project3DTo2D(totalLength, 0, 0, params); // X轴向右延伸，使用正的totalLength
  const endXZ = project3DTo2D(0, 0, 0, params);
  pathData += ` L ${startXZ.x},${startXZ.y} L ${endXZ.x},${endXZ.y} Z`;
  path.setAttribute('d', pathData);
}

3D 旋转

这个例子的场景非常简单，因此无需使用 three.js 之类的 3D 库就可以实现 3D 效果，需要的是用数学进行坐标变换。

例如，让 xOy 平面中的一个点 (x,y) 绕 + z 轴（图中未画出，垂直纸面向外，根据右手螺旋定则，四指从 + x 轴转向 + y 轴，若大拇指指向 + z 轴方向，则这个坐标系为右手坐标系，反之则为左手坐标系）逆时针旋转 θ，这个点的坐标会变为 (xʹ,yʹ)，如下图所示：

若原来的坐标用极坐标表示为：

\[x = r\cos \varphi ,y = r\sin \varphi \]

则旋转后的坐标为：

\[x' = r\cos (\varphi + \theta ),y' = r\sin (\varphi + \theta )\]

利用三角和差公式可求得变换公式：

\[x' = r\cos (\varphi + \theta ) = r\cos \varphi \cos \theta - r\sin \varphi \sin \theta = x\cos \theta - y\sin \theta \]

\[y' = r\sin (\varphi + \theta ) = r\sin \varphi \cos \theta + r\cos \varphi \sin \theta = x\sin \theta + y\cos \theta \]

对应的代码如下：

// 3D到2D投影函数 - 右手坐标系实现（正交投影）
function project3DTo2D(x, y, z, params) {
    // 将角度转换为弧度
    const radX = params.rotateX * Math.PI / 180;
    const radY = params.rotateY * Math.PI / 180;

    // 1. 先绕世界坐标系的Y轴旋转
    let x1 = x * Math.cos(radY) - z * Math.sin(radY);
    let z1 = x * Math.sin(radY) + z * Math.cos(radY);
    let y1 = y;

    // 2. 再绕世界坐标系的X轴旋转
    let y2 = y1 * Math.cos(radX) - z1 * Math.sin(radX);
    let z2 = y1 * Math.sin(radX) + z1 * Math.cos(radX);
    let x2 = x1;

    // 直接使用X轴旋转后的结果
    let x3 = x2;
    let y3 = y2;
    let z3 = z2;

    // 正交投影 - 不使用透视缩放，直接映射
    // SVG坐标系中Y轴向下，所以需要取反使3D Y轴向上
    const projectedX = x3;
    const projectedY = -y3; // 使用y3而不是y2，确保Y轴旋转被正确应用

    // 使用viewBox的固定尺寸作为中心（1400x1040）
    const svgCenterX = 400; // X轴方向原点距离左侧400个单位
    const svgCenterY = 470; // Y轴下移到470（比之前再下移50px）

    return {
    x: projectedX + svgCenterX,
    y: projectedY + svgCenterY,
    depth: z3 // 用于深度排序（如果需要）
};

用图形学的说法是，上面的公式只是将模型坐标系转换到了世界坐标系，接下来还需要透视变换和观察变换，这里使用的是正交投影，无需近大远小的透视效果，所以无需变换。（想深入了解可见 Direct3D 11 教程 4：3D 空间，其中的数学原理可见 5.6 顶点着色器阶段）

可以发明一种表达式把上面的式子

\[\begin{array}{l}x' = x\cos \theta - y\sin \theta \\y' = x\sin \theta + y\cos \theta \end{array}\]

简化一下写成

\[\left[ {\begin{array}{*{20}{c}}{x'}\\{y'}\end{array}} \right] = \left[ {\begin{array}{*{20}{c}}{\cos \theta }&{ - \sin \theta }\\{\sin \theta }&{\cos \theta }\end{array}} \right]\left[ {\begin{array}{*{20}{c}}x\\y\end{array}} \right]\]

右边四四方方的东西就把它叫做矩阵吧，右边两块的写法看着像“乘法”，然后自定义这个“乘法”的运算法则为：左边第一行的数字 xʹ = 右边矩阵第一行的两个元素量 cosθ、– sinθ 分别乘以第一列的两个数字 x、y 的和，即 xʹ = xcosθ + (– ysinθ)，yʹ 也做类似的处理。

就这样，我独立发明了矩阵运算！呵呵！

量子力学的奠基人之一海森堡也有类似的经历！1925 年，因花粉过敏，他独自前往北海的黑尔戈兰岛休养。在远离人群的宁静环境中，他集中思考了当时原子理论中的矛盾，用可观测的谱线频率和强度（而不是不可见的电子轨道）来构建原子理论。他引入了一种新的“量子理论中的乘法规则”，用于计算这些可观测量。他注意到，在他的新乘法规则下，两个量的乘积依赖于顺序，即 A×B ≠ B×A。这让他很困惑，因为经典物理中的量都是对易的。但他发现，只有这样，才能导出正确的能量守恒等物理结果。

海森堡对自己的数学处理并不完全自信，他把论文草稿交给了他的上级——马克斯·玻恩，一位熟悉数学物理的教授。玻恩看到海森堡的乘法规则后，立刻认出了这是矩阵乘法。玻恩曾在大学学习过矩阵理论（当时矩阵在物理中很少用），他意识到海森堡无意中重新发明了矩阵代数。玻恩随后与他的年轻助手帕斯库尔·约旦合作，用严谨的矩阵语言重新表述了海森堡的思想，并引入了关键的对易关系 pq – qp = \(\dfrac{h}{{2\pi i}}\)，从而建立了系统的“矩阵力学”，这成为量子力学的核心，与薛定谔的波动力学共同构成量子力学的两种等价形式。

上式中 p 是动量算符（在量子力学中它作用于系统的态，不再是一个简单的数）；q 是位置算符。在矩阵力学中，p 和 q 都是矩阵（无限维矩阵）。pq – qp 表示“先作用 q 再作用 p”与“先作用 p 再作用 q ”的差别。

在经典力学里，一个粒子的位置 q 和动量 p 只是普通的数值，乘法可以交换顺序，即 pq – qp = 0。但在量子力学中，测量位置和动量的顺序会影响结果，这导致了一个根本的不确定性。具体来说，这个公式意味着：你不可能同时精确确定一个粒子的位置和动量；如果位置测量越精确，动量就越不确定，反之亦然。这就是著名的海森堡不确定性原理 Δx·Δp ≥ \(\frac{h}{{4\pi }}\) 的数学根源。

在“远古时期”，线框（Wireframe）3D 游戏是计算机图形发展史上的重要里程碑，它们在硬件性能极其有限的时代，通过使用上面类似的巧妙算法实现了令人惊叹的 3D 效果。例如 1983 年由雅达利（Atari）开发的街机游戏《星球大战》（Star Wars），其中的所有物体——你的X翼战机、钛战机、死星表面、炮塔、爆炸效果——全部由极其明亮、锐利、流畅的颜色线条在黑色背景上构成，如下图所示。

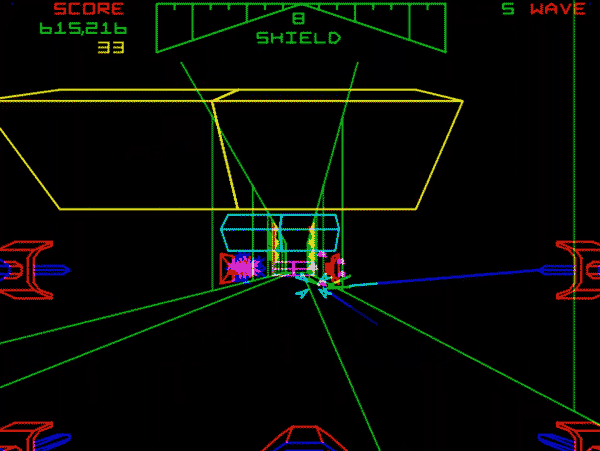
上述算法在图形学里被称为顶点变换，将模型的顶点从本地坐标转换到屏幕坐标，这个课件每帧要使用 CPU 进行 400 多次变换运算。现如今一个游戏中的某个人物大概就要用到 10 万个左右的顶点，不过这些计算都已经移至显卡 GPU 上了，CPU 很难快速处理这么多的顶点。世界上第一块支持硬件 T&L（Transform and Lighting，坐标变换与光照处理）的消费级显卡是 NVIDIA GeForce 256，它是于 1999 年 8 月 31 日发布的。

为什么早期的 3D 画面往往是线框模型，因为上面的算法无法解决遮挡问题，你会发现上面游戏截图中前方的物体是透明的，无法将后面的物体挡住。要解决这个问题，可以存储顶点的z坐标值，然后根据这个坐标进行排序，由远及近地绘制每个图形，而现代显卡通常采用深度缓冲（Z-Buffer）的方法。

在这个课件中，先绘制红色正弦波，再绘制蓝色正弦波，这会导致蓝色波总是覆盖在红色波的上方。在初始状态中，通过设置观察角度隐藏了这个缺陷，若你将 3D 图形旋转到一定角度就会露馅，不过课件中还将颜色设置了半透明效果，不仔细看是看不出这个破绽的。在课件中 project3DTo2D 方法中还返回了 “depth: z3 // 用于深度排序（如果需要）”，但没有用它进行遮挡处理。

完整代码

code

发布时间：2026/2/5 下午6:13:59  阅读次数：25