5.6 顶点着色器阶段

5.6.1 局部空间和世界空间
5.6.2 观察空间
5.6.3 投影与齐次裁剪空间

在完成图元装配后，顶点将被送往顶点着色器（vertex shader）阶段。顶点着色器可以被看成是一个以顶点作为输入输出数据的函数。每个将要绘制的顶点都会通过顶点着色器推送至硬件；实际上，我们可以概念性地认为在硬件上执行了如下代码：

for(UINT i = 0; i < numVertices; ++i)
    outputVertex[i] = VertexShader(inputVertex[i]);

顶点着色器函数由我们自己编写，但是它会在GPU上运行，所以执行速度非常快。

许多效果，比如变换（transformation）、光照（lighting）和置换贴图映射（displacement mapping）都是由顶点着色器来实现的。记住，在顶点着色器中，我们不仅可以访问输入的顶点数据，也可以访问在内存中的纹理和其他数据，比如变换矩阵和场景灯光。

我们将会在本书中看到许多不同的顶点着色器示例；当读完本书时，读者会对顶点着色器的功能有一个全面的认识。不过，我们的第一个示例会比较简单，只是用顶点着色器实现顶点变换。在随后的小节中，我们将讲解各种常用的变换算法。

5.6.1 局部空间和世界空间

现在让我们来假设一个情景：你正在参与一部影片的拍摄工作，剧组要为拍摄某些特殊效果而搭建一个微缩场景。你的具体任务是搭建一座小桥。现在，你不能在场景中搭建小桥，你必须另选地点，在远离场景的地方建立工作台，制作小桥，以避免弄乱场景中的其他微缩物品。当小桥建成后，你要按照正确的位置和角度把小桥放到场景中。

3D美术师在创建3D场景时也采用同样的工作方式。他们不在全局场景坐标系（world space，世界空间）中建立物体，而是在局部坐标系（local space，局部空间）中建立物体；局部坐标系是最常用的实用坐标系，它的原点接近于物体中心，坐标轴的方向与物体的方向对齐。在完成3D模型的制作之后，美术师会将模型放到全局场景中；通过计算局部坐标系相对于世界坐标系的原点和轴向，实现相应的坐标转换变换（参见图5.16，并回顾3.4节的内容）。将坐标从局部坐标系转换到世界坐标系的过程称为世界变换（world transform），相应的变换矩阵称为世界矩阵（world matrix）。当所有的物体都从局部空间变换到世界空间后，这些物体就会位于同一个坐标系（世界空间）中。如果你希望直接在世界空间中定义物体，那么可以使用单位世界矩阵（identity world matrix）。

图5.16 — 图 5.16 (a)物体的每个顶点都是相对于它们自己的局部坐标系来定义的。我们根据物体在场景中的位置和方向来定义每个局部坐标系相对于世界坐标系的位置和方向。然后我们执行坐标转换变换，将所有坐标转换到世界坐标系中。(b)在世界变换后，所有物体的顶点都会位于同一个世界坐标系中。

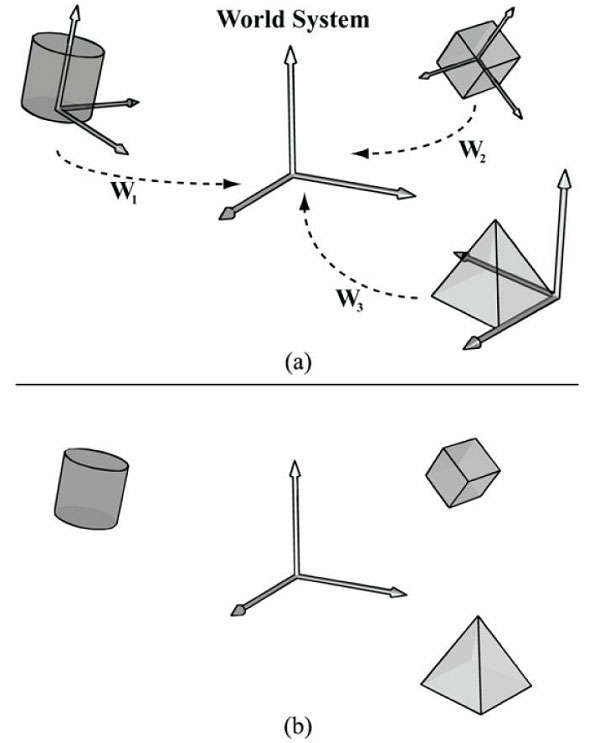
根据模型自身的局部坐标系定义模型，有以下几点好处：

1．简单易用。比如，在局部坐标系中，坐标系的原点通常会与物体的中心对齐，而某个主轴可能正是物体的对称轴。又如，当我们使用局部坐标系时，由于坐标系的原点与立方体的中心对齐，坐标轴垂直于立方体表面，所以可以更容易地描述立方体的顶点（参见图5.17）。

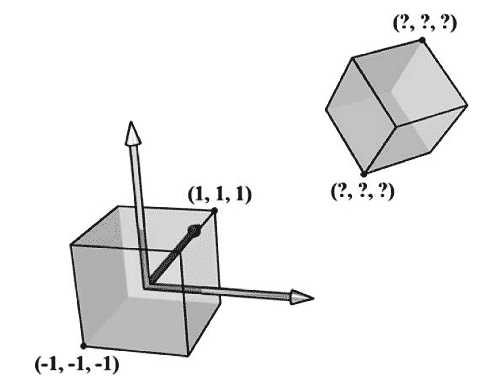
2．物体可以在多个场景中重复使用，对物体坐标进行相对于特定场景的硬编码是毫无意义的事情。较好的做法是：在局部坐标系中存储物体坐标，通过坐标转换矩阵将物体从局部坐标系变换到世界坐标系，建立物体与场景之间的联系。

3．最后，有时我们会多次绘制相同的物体，只是物体的位置、方向和大小有所不同（比如，将一棵树重绘多次形成一片森林）。在这种情况下，我们只需要一个相对于局部坐标系的单个副本，而不是多次复制物体数据，为每个实例创建一个副本。当绘制物体时，我们为每个物体指定不同的世界矩阵，改变它们在世界空间中的位置、方向和大小。这种方法叫做instancing。

如3.4.3节所述，世界矩阵描述的是一个物体的局部空间相对于世界空间的原点位置和坐标轴方向，这些坐标可以存放在一个行矩阵中。设Q_w = (Q_x,Q_y ,Q_z ,1)、u_w= (u_x ,u_y ,u_z ,0)、v_w= (v_x ,v_y ,v_z ,0)、w_w = (w_x ,w_y,w_z ,0)分别表示局部空间相对于世界空间的原点、x轴、y轴、z轴的齐次坐标，由3.4.3节可知，从局部空间到世界空间的坐标转换矩阵为：

\({\bf{W}} = \left( {\begin{array}{*{20}{c}}{{u_x}}&{{u_y}}&{{u_z}}&0\\{{v_x}}&{{v_y}}&{{v_z}}&0\\{{w_x}}&{{w_y}}&{{w_z}}&0\\{{Q_x}}&{{Q_y}}&{{u_z}}&1\end{array}} \right)\)

示例

假设一个正方形的顶点局部坐标在(−0.5,0,−0.5)和(0.5,0,0.5)之间，将它的边长变为2，顺时针旋转45°，并放置在世界空间的（10,0,10）坐标上，那如何求它在世界空间中的坐标呢？我们需要构建S，R，T矩阵，世界矩阵W如下所示：

\({\bf{S}} = \left( {\begin{array}{*{20}{c}}2&0&0&0\\0&1&0&0\\0&0&2&0\\0&0&0&1\end{array}} \right)\)\({\bf{R}} = \left( {\begin{array}{*{20}{c}}{\sqrt 2 /2}&0&{ - \sqrt 2 /2}&0\\0&1&0&0\\{\sqrt 2 /2}&0&{\sqrt 2 /2}&0\\0&0&0&1\end{array}} \right)\)\({\bf{T}} = \left( {\begin{array}{*{20}{c}}1&0&0&0\\0&1&0&0\\0&0&1&0\\{10}&0&{10}&1\end{array}} \right)\)

\({\bf{W}} = {\bf{SRT}} = \left( {\begin{array}{*{20}{c}}{\sqrt 2 }&0&{ - \sqrt 2 }&0\\0&1&0&0\\{\sqrt 2 }&0&{\sqrt 2 }&0\\10&0&10&1\end{array}} \right)\)

根据3.5节的讲解，W中的行表示相对于世界空间的局部坐标系；即u_w=(2 ,0, -2 ,0)，v_w=(0,1,0 ,0)，w_w=(2 ,0, 2 ,0)，Q_w=(10,0, 10,1)。当我们使用W将局部坐标系转换到世界坐标系时，正方形就会处在期望的位置上（见图5.18）。

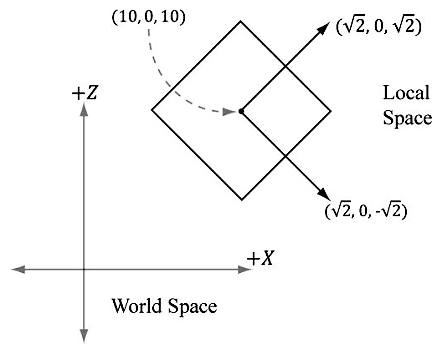
这个例子的要点是无需计算Q_w，u_w，v_w，w_w直接获得世界矩阵，而是通过组合一系列简单的变换矩阵获得世界矩阵，这通常比直接求解Q_w，u_w，v_w，w_w简单。我们只需确定：物体在世界空间中的尺寸多大，在世界空间中的朝向如何，我们要将该物体放置在世界空间中的何处。

还有一种考虑世界变换的方式是：只考虑局部坐标并把它作为世界坐标对待（这相当于使用一个单位矩阵作为世界变换矩阵）。这样，如果物体建模时就位于局部坐标的原点，那么它也在世界空间的坐标原点。通常，世界空间的坐标原点并不是我们想放置物体的位置，所以，对每个物体，我们只要施加一组变换用于缩放、选择、平移，将物体放置在世界空间中的确定位置。从数学上来说，这与将矩阵从局部空间转换到世界空间的变换效果是相同的。

5.6.2 观察空间

为了生成场景的2D图像，我们必须在场景中放置一架虚拟摄像机。虚拟摄像机指定了观察者可以看到的场景范围，或者说是我们所要生成的2D图像所显示的场景范围。我们把一个局部坐标系（称为观察空间、视觉空间或摄像机空间）附加在摄像机上，如图5.19所示；该坐标系以摄像机的位置为原点，以摄像机的观察方向为z轴正方向，以摄像机的右侧为x轴，以摄像机的上方为y轴。在渲染管线的随后阶段中，使用观察空间来描述顶点比使用世界空间来描述顶点要方便的多。从世界空间到观察空间的坐标转换称为观察变换（view transform），相应的矩阵称为观察矩阵（view matrix）。

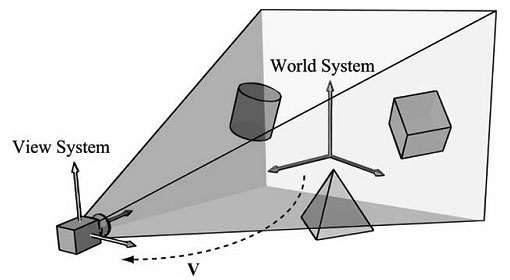
设Q_w = (Q_x,Q_y ,Q_z ,1)、u_w= (u_x ,u_y ,u_z ,0)、v_w= (v_x ,v_y ,v_z ,0)、w_w = (w_x ,w_y,w_z ,0)分别表示观察空间相对于世界空间的原点、x轴、y轴、z轴的齐次坐标，我们由3.4.3节可知，从观察空间到世界空间的坐标转换矩阵为：

\({\bf{W}} = \left[ {\begin{array}{*{20}{c}}{{u_x}}&{{u_y}}&{{u_z}}&0\\{{v_x}}&{{v_y}}&{{v_z}}&0\\{{w_x}}&{{w_y}}&{{w_z}}&0\\{{Q_x}}&{{Q_y}}&{{u_z}}&1\end{array}} \right]\)

不过，这不是我们想要的结果。我们希望得到的是从世界空间到观察空间的反向变换。回顾3.4.5节可知，反向变换可由逆运算取得。也就是，W^-1为世界空间到观察空间的变换矩阵。

世界坐标系和观察坐标系通常具有不同的位置和方向，所以凭直觉就可以知道W = RT的含义（即，世界矩阵可以被分解为一个旋转矩阵和一个平移矩阵）。这种方式可以使逆矩阵的计算过程更简单一些：

V = W^-1 = (RT)^-1 = T^-1R^-1 = T^-1R^T

\({\rm{ = }}\left[ {\begin{array}{*{20}{c}}1&0&0&0\\0&1&0&0\\0&0&1&0\\{ - {Q_x}}&{ - {Q_y}}&{ - {Q_z}}&1\end{array}} \right]\left[ {\begin{array}{*{20}{c}}{{u_x}}&{{v_x}}&{{w_x}}&0\\{{u_y}}&{{v_y}}&{{w_y}}&0\\{{u_z}}&{{v_z}}&{{w_z}}&0\\0&0&0&1\end{array}} \right] = \left[ {\begin{array}{*{20}{c}}{{u_x}}&{{v_x}}&{{w_x}}&0\\{{u_y}}&{{v_y}}&{{w_y}}&0\\{{u_z}}&{{v_z}}&{{w_z}}&0\\{ - {\bf{Q}} \cdot {\bf{u}}}&{ - {\bf{Q}} \cdot {\bf{v}}}&{ - {\bf{Q}} \cdot {\bf{w}}}&1\end{array}} \right]\)

所以，观察矩阵为：

\({\bf{V}} = \left[ {\begin{array}{*{20}{c}}{{u_x}}&{{v_x}}&{{w_x}}&0\\{{u_y}}&{{v_y}}&{{w_y}}&0\\{{u_z}}&{{v_z}}&{{w_z}}&0\\{ - {\bf{Q}} \cdot {\bf{u}}}&{ - {\bf{Q}} \cdot {\bf{v}}}&{ - {\bf{Q}} \cdot {\bf{w}}}&1\end{array}} \right]\)

我们现在介绍一种更直观的方法来创建构成观察矩阵的向量。设Q为摄像机的位置，T为摄像机瞄准的目标点，j为描述世界空间“向上”方向的单位向量。参考图5.20，摄像机的观察方向为：

\({\bf{w}}{\rm{ = }}\frac{{{\bf{T}} - {\bf{Q}}}}{{\left\| {{\bf{T}} - {\bf{Q}}} \right\|}}\)

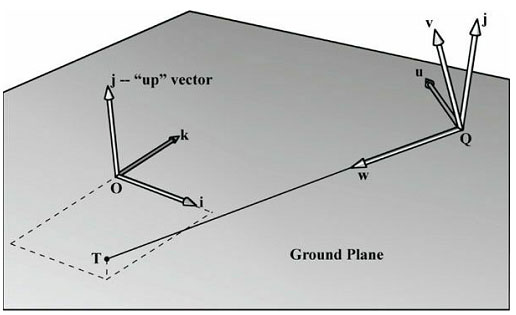
向量w描述的是摄像机坐标系的z轴。指向w“右边”的单位向量为：

\({\bf{u}}{\rm{ = }}\frac{{{\bf{j}} \times {\bf{w}}}}{{\left\| {{\bf{j}} \times {\bf{w}}} \right\|}}\)

向量u描述的是摄像机坐标系的x轴。最后，描述摄像机坐标系y轴的向量为：

v=w×u

由于w和u是相互垂直的单位向量，所以w×u必定为单位向量，不需要对它做规范化处理。

这样，给出摄像机的位置、目标点和世界“向上”向量，我们就能够得到摄像机的局部坐标系，该坐标系可以用于创建观察矩阵。

XNA库提供了如下函数，根据刚才描述的过程计算观察矩阵：

XMMATRIX XMMatrixLookAtLH( // Outputs resulting view matrix V
    FXMVECTOR EyePosition,   // Input camera position Q
    FXMVECTOR FocusPosition,   // Input target point T
    FXMVECTOR UpDirection);  // Input world up vector j

通常，世界坐标系的y轴就是“向上”方向，所以“向上”向量j通常设为(0, 1,0)。举一个例子，假设摄像机相对于世界空间的位置为(5, 3, −10)，目标点为世界原点(0, 0,0)。我们可以使用如下代码创建观察矩阵：

XMVECTOR pos = XMVectorSet(5,3,-10,1.0f);
XMVECTOR target = XMVectorZero();
XMVECTOR up = XMVectorSet(0.0f,1.0f,0.0f,0.0f);
XMMATRIXV = XMMatrixLookAtLH(pos,target,up);

5.6.3 投影与齐次裁剪空间

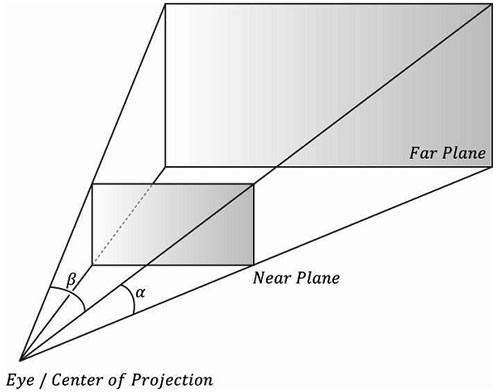
到目前为止，我们已经知道了如何在场景中描述摄像机的位置和方向，下面我们来讲解如何描述摄像机所能看到的空间范围。该范围通过一个平截头体（frustum）来描述（图5.21），它是一个在近平面处削去尖部的棱锥体。

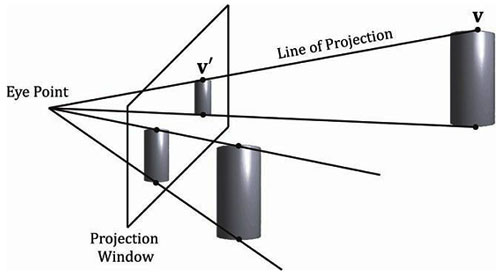
我们的下一个任务是把平截头体内的3D物体投影到2D投影窗口上。投影（projection）必须按照平行线汇集为零点的方式来实现，随着一个物体的3D深度增加，它的投影尺寸会越来越小；图5.22说明了透视投影的实现过程。我们将“从顶点连向观察点的直线”称为顶点的投影线。然后我们可以定义透视投影变换，将3D顶点v变换到它的投影线与2D投影平面相交的点vʹ上；我们将vʹ称为v的投影。对一个3D物体的投影就是对组成该物体的所有顶点的投影。

5.6.3.1 定义平截头体

我们可以在观察空间中使用如下4个参数来定义以原点为投影中心、以z轴正方向为观察方向的平截头体：近平面n、远平面f、垂直视域角α和横纵比r。注意，在观察空间中，近平面和远平面都平行于xy平面；所以，我们只需要简单地指定它们沿z轴方向到原点之间的距离即可表示这两个平面。横纵比由r = w/ℎ定义，其中w表示投影窗口的宽度，ℎ表示投影窗口的高度（单位由观察空间决定）。投影窗口本质上是指场景在观察空间中的2D 图像。该图像最终会被映射到后台缓冲区中；所以，我们希望投影窗口的尺寸比例与后台缓冲区的尺寸比例保持相同。在大多数情况下，横纵比就是指后台缓冲区的尺寸比例（它是一个比例值，所以没有单位）。例如，当后台缓冲区的尺寸为800×600时，横纵比r = 800/600 ≈ 1.333。如果投影窗口的横纵比与后台缓冲区的横纵比不同，那么当投影窗口映射到后台缓冲区时，必然会出现比例失衡，导致图像变形（例如，投影窗口中的一个正圆会被拉伸为后台缓冲区中的一个椭圆）。

将水平视域角设为β，它是由垂直视域角α和横纵比r决定的。考虑图5.23，分析一下如何通过α、r来求解β。注意，投影窗口的实际尺寸并不重要，重要的只是横纵比。所以，我们将高度设定为2，则对应的宽度为：

r=w/h =w/2 ⟹ w=2r

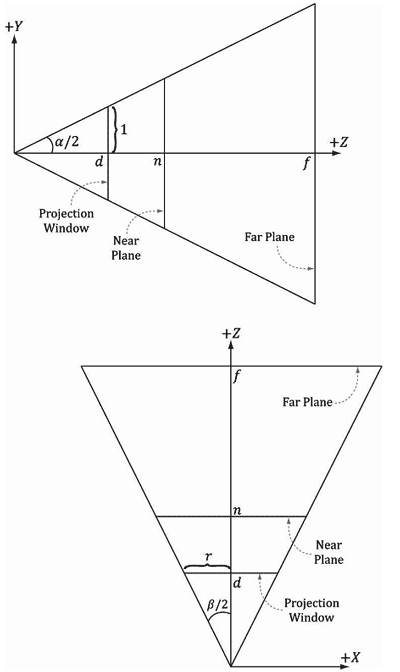
为了获得指定的垂直视域角α，投影窗口必须放在与原点距离为d的位置上：

tan(α/2) = 1/d ⟹ d = cot(α/2)

观察图5.23中的xz平面，可知：

tan(β/2) = r/d = r / cot(α/2) = r•tan(α/2)

所以，只要给出垂直视域角α和横纵比r，我们就能求出水平视域角β。

β = 2tan^-1（r•tan(α/2) ）

5.6.3.2 对顶点进行投影

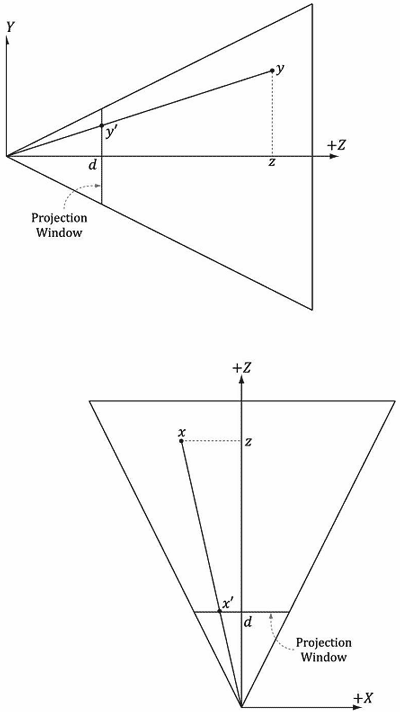
参见图5.24。给出一个点 (x, y, z)，求它在投影平面z = d上的投影点 (xʹ, yʹ, d)。通过分析x、y坐标以及使用相似三角形，我们可以求出：

xʹ/d =x/z ⟹ xʹ = xd/z = x cot(α/2) /z = x/ztan(α/2)

和

yʹ/d =y/z ⟹ yʹ = yd/z = y cot(α/2)/ z = y/ztan(α/2)

当且仅当以下条件成立时，点(x, y , z)在平截头体内。

−r ≤ xʹ ≤ r

−1 ≤ yʹ ≤ 1

n ≤ z ≤ f

5.6.3.3 规范化设备坐标（NDC）

上一节我们讲解了如何在观察空间中计算点的投影坐标。在观察空间中，投影窗口的高度为2，宽度为2r，其中r表示横纵比。这里存在的一个问题是：尺寸依赖于横纵比。这意味着我们必须为硬件指定横纵比，否则硬件将无法执行那些与投影窗口尺寸相关的运算（比如，将投影窗口映射到后台缓冲区）。如果我们能去除对横纵比的依赖性，那么会使相关的运算变得更加简单。为了解决一问题，我们将的投影x坐标从[−r , r] 区间缩放到[−1,1]区间：

−r ≤ xʹ ≤ r

−1 ≤ xʹ ⁄r ≤ 1

在映射之后，x、y坐标称为规范化设备坐标（normalized device coordinates，简称NDC）（z坐标还没有被规范化）。当且仅当以下条件成立时，点(x ,y, z)在平截头体内。

−1 ≤ xʹ⁄r ≤ 1

−1 ≤ yʹ ≤ 1

n ≤ z ≤ f

从观察空间到NDC空间的变换可以看成是一个单位转换。我们有这样一个关系式：在 x轴上的一个NDC单位等于观察空间中的r个单位（即，1 ndc = r vs）。所以给出x观察空间单位，我们可以使用这个关系式来转换单位：

x vs \(\frac{{1{\rm{ nds}}}}{{{\rm{r vs}}}}\) = \(\frac{x}{r}\) ndc

我们可以修改之前的投影公式，直接使用NDC空间中的x、y投影坐标：

\(x' = \frac{x}{{rz\tan \frac{\alpha }{2}}}\)

\(y' = \frac{y}{{z\tan \frac{\alpha }{2}}}\)（方程5.1）

注意：在NDC空间中，投影窗口的高度和宽度都为2。也就是说，现在的尺寸是固定的，硬件不需要知道横纵比，但是我们必须自己来完成投影坐标从观察空间到NDC空间的转换工作（图形硬件假定我们会完成一工作）。

5.6.3.4 用矩阵来描述投影方程

为了保持一致，我们将用一个矩阵来描述投影变换。不过，方程5.1是非线性的，无法用矩阵描述。所以我们要使用一种“技巧”将它分为两部分来实现：一个线性部分和一个非线性部分。非线性部分要除以z。我们会在下一节讨论“如何规范化z坐标”时讲解这一问题；现在读者只需要知道，我们会因为个除法操作而失去原始的z坐标。所以，我们必须在变换之前保存输入的z坐标；我们可以利用齐次坐标来解决一问题，将输入的z坐标复制给输出的w坐标。在矩阵乘法中，我们要将元素[2][3]设为1、元素[3][3]设为0（从0开始的索引）。我们的投影矩阵大致如下：

\({\bf{P}} = \left[ {\begin{array}{*{20}{c}}{\frac{1}{{r\tan \frac{\alpha }{2}}}}&0&0&0\\0&{\frac{1}{{\tan \frac{\alpha }{2}}}}&0&0\\0&0&A&1\\0&0&B&0\end{array}} \right]\)

注意矩阵中的常量A和B（它们将在下一节讨论）；这些常量用于把输入的z坐标变换到规范化区间。将一个任意点(x , y, z,1)与该矩阵相乘，可以得到：

\(\left[ {x,y,z,1} \right]\left[ {\begin{array}{*{20}{c}}{\frac{1}{{r\tan \frac{\alpha }{2}}}}&0&0&0\\0&{\frac{1}{{\tan \frac{\alpha }{2}}}}&0&0\\0&0&A&1\\0&0&B&0\end{array}} \right] = \left[ {\frac{x}{{r\tan \frac{\alpha }{2}}},\frac{y}{{\tan \frac{\alpha }{2}}},Az + B,z} \right]\)（公式5.2）

在与投影矩阵（线性部分）相乘之后，我们要将每个坐标除以w = z（非线性部分），得到最终的变换结果：

\(\left[ {\frac{x}{{r\tan \frac{\alpha }{2}}},\frac{y}{{\tan \frac{\alpha }{2}}},Az + B,z} \right] \to \left[ {\frac{x}{{rz\tan \frac{\alpha }{2}}},\frac{y}{{z\tan \frac{\alpha }{2}}},A + \frac{B}{z},1} \right]\)（公式5.3）

顺便提一句，你可能会问：“如何处理除数为0的情况”；对于一问题我们不必担心，因为近平面总是大于0的，其他的点都会被裁剪掉（参见5.9节）。有时，与w相除的过程也称为透视除法（perspective divide）或齐次除法（homogeneous divide）。我们可以看到x、y的投影坐标与方程5.1相同。

5.6.3.5 规范化深度值

你可能认为在投影之后可以丢弃原始的3D z坐标，因为所有的投影点已经摆放在2D投影窗口上，形成了我们最终看到的2D图像，不会再使用3D z坐标了。其实不然，我们仍然需要为深度缓存算法提供3D深度信息。就如同Direct3D希望我们把x、y投影坐标映射到一个规范化区间一样，Direct3D也希望我们将深度坐标映射到一个规范化区间[0,1]中。所以，我们需要创建一个保序函数（order preserving function）g(x)把[n,f]区间映射到[0,1]区间。由于该函数是保序的，所以当z₁,z₂∈[n,f]且z₁<z₂时，必有g(z₁)<g(z₂)。这样，即使深度值已经被变换过了，相对的深度关系还是会被完好无损地保留下来，我们依然可以在规范化区间中得到正确的深度测试结果，这就是我们要为深度缓存算法做的全部工作。

通过缩放和平移可以实现从[n ,f]到[0,1]的映射。但是，这种方式无法与我们当前的投影方程整合。我们可以从方程5.3中看到经过变换的z坐标为：

g(z) = A+B/z

我们现在需要让A和B满足以下条件：

条件1：g(n) = A + B/n = 0（近平面映射为0）
条件2：g(f) = A +B/f = 1（远平面映射为1）

由条件1得到B的结果为：B= −An。把它代入条件2，得到A的结果为：

\(\begin{array}{l}A + \frac{{ - An}}{f} = 1\\\frac{{Af - An}}{f} = 1\\A = \frac{f}{{f - n}}\end{array}\)

所以，

\(g(z) = \frac{f}{{f - n}} - \frac{{nf}}{{(f - n)z}}\)

从g(z)的曲线图（图5.25）中可以看出，它会限制增长的幅度（保序）而且是非线性的。从图中我们还可以看到，区间中的大部分取值落在近平面附近。因此，大多数深度值被映射到了一个很窄的取值范围内。这会导致深度缓冲区出现精度问题（由于所能表示的数值范围有限，计算机将无法识别变换后的深度值之间的微小差异）。通常的建议是让近平面和远平面尽可能接近，把深度的精度性问题减小到最低程度。

现在我们已经解出了A和B，我们可以确定出完整的透视投影矩阵：

\({\bf{P}} = \left[ {\begin{array}{*{20}{c}}{\frac{1}{{r\tan \frac{\alpha }{2}}}}&0&0&0\\0&{\frac{1}{{\tan \frac{\alpha }{2}}}}&0&0\\0&0&{\frac{f}{{f - n}}}&1\\0&0&{\frac{{ - nf}}{{f - n}}}&0\end{array}} \right]\)

在与投影矩阵相乘之后，进行透视除法之前，几何体所处的空间称为齐次裁剪空间（homogeneous clip space）或投影空间（projection space）。在透视除法之后，几何体所处的空间称为规范化设备空间（normalized device coordinates，简称NDC）。

5.6.3.6 XMMatrixPerspectiveFovLH

透视投影矩阵可由如下XNA函数生成：

XMMATRIX XMMatrixPerspective FovLH(// returns projection matrix
     FLOAT FovAngleY, // vertical field of view angle in radians
     FLOAT AspectRatio, // aspect ratio =  width / height
     FLOAT NearZ, // distance to near plane
     FLOAT FarZ);  // distance to far plane

下面的代码片段示范了XMMatrixPerspectiveFovLH函数的使用方法。这里，我们将垂直视域角设为45°，近平面z设为1，远平面z设为1000（这些长度是在观察空间中的）。

XMMATRIX P = XMMatrixPerspectiveFovLH(0.25f*MathX::Pi,
     AspectRatio(),1.0f,1000.0f);

横纵比要匹配窗口的横纵比：

float D3Dapp::AspectRatio() const
{
     return static_cast<float>(mClientWidth)/mClientHeight;
}

文件下载（已下载 1673 次）

发布时间：2014/7/28 下午8:35:14 阅读次数：7781