使用 Geogebra 检验恒功率启动的计算结果

继在“使用 Geogebra 解常微分方程”中检验电磁感应中恒力启动问题之后，这篇文章对交通工具的恒功率启动问题进行检验，在高中阶段的此类问题中，一旦涉及到“多久、多远后达到稳定速度”的数值计算题，往往是错题的重灾区。

1、理论推导

质量为 m 汽车的额定功率为 P，运动过程中受到恒定阻力 f，汽车运动的初速度为 v₀，在运动过程中满足牛顿第二定律 F – f = ma，且 P = Fv，可得：

\(\frac{P}{v}\) − f = ma

对应的微分方程为：

m \(\frac{{{\rm{d}}v}}{{{\rm{d}}t}}\) = \(\frac{P}{v}\) − f

分离变量得：

\(\frac{1}{m}\) dt = \(\frac{v}{{P - fv}}\) dv

两边积分（右侧的积分可利用 \(\int {\frac{x}{{ax + b}}{\rm{d}}x}  = \frac{1}{{{a^2}}}(ax + b - b\ln \left| {ax + b} \right| ) + C\) 解决）可得：

\(\frac{1}{m}\) t = \(\frac{1}{{{f^2}}}\) [ P – fv −P ln(P – fv) ] + C

考虑初始条件为：t = 0 时，v = v₀，解得常数 C 为 − \(\frac{1}{{{f^2}}}\) [ P – fv₀ −P ln(P – fv₀) ]，代入上式得：

\[t = \frac{{mP}}{{{f^2}}}\ln \frac{{P - f{v_0}}}{{P - fv}} - \frac{{m(v - {v_0})}}{f}\]

2、在 Geogebra 中的实现

由理论推导出了 t – v 函数，就可以用来进行数值计算，其实用 excel 也可以完成相同的工作，但 Geogebra 有滑动条，可以直观、动态地改变输入参数，使用比较方便。

更符合使用习惯的是 v – t 函数图像，但是上述 t - v 函数的反函数无法用初等函数表示，上网查了一下，v – t 函数的表达要涉及一个叫做 Lambert W 函数的特殊函数：W(x)e^W(x) = x，所以目前在 Geogebra 中只能绘制出 t - v 图像。

为了适用不同的数据，并没有直接将 P、f 作为输入参数，而是适当变形。由于 a = \(\frac{P}{m}\)·\(\frac{1}{v}\) − \(\frac{f}{m}\)，可以令 k = \(\frac{P}{m}\)，b = \(\frac{f}{m}\)，这样将前面的理论推导变化为：

\[t = \frac{k}{{{b^2}}}\ln \frac{{k - b{v_0}}}{{k - bv}} - \frac{{v - {v_0}}}{b}\]

在 Geogebra 中的操作步骤如下：

1、设置滑动条 k、b、v0、m 和 v；

2、输入函数表达式：f(x)=如果(x≥v0, ((k)/(b^(2))) ln(((k-b v0)/(k-b x)))-((x-v0)/(b)))；

3、设置变量 t = f(v)，求速度为 v 时所用时间；

4、输入：s = 积分(f,v0,v)；设置变量 S = vt - s，求物体走过的位移。说明：积分求得的 t – v 图像的面积，而我们要求的是 v – t 图像的面积，因此需要用矩形面积 vt 减去积分面积。

3、在 Geogebra 中验证

例 1

此题为 2009 年上海高考题。

质量为 5×10³ kg 的汽车在 t = 0 时刻速度 v₀ = 10 m/s，随后以 P = 6×10⁴ W 的额定功率沿平直公路继续前进，经 72 s 达到最大速度，设汽车受恒定阻力，其大小为 2.5×10³ N。求：

（1）汽车的最大速度 v_m；

（2）汽车在 72 s 内经过的路程 s。

参考答案：（1）v_m = 24 m/s          （2）s = 1252 m

【分析】

（1）汽车达到最大速度时，牵引力等于阻力，此时

P ＝ fv_m，v_m ＝ \(\frac{P}{f}\) ＝ \(\frac{{6 \times {{10}^4}}}{{2.5 \times {{10}^3}}}\) m/s ＝ 24 m/s

（2）由动能定理得

Pt − fs ＝ \(\frac{1}{2}\) mv_m² − \(\frac{1}{2}\) mv₀²

s ＝ \(\frac{{2Pt - mv_m^2 + mv_0^2}}{{2f}}\) ＝ 1252 m

【验证】

此题中，k = \(\frac{P}{m}\) = 12，b = \(\frac{f}{m}\) = 0.5。在 Geogebra 中将滑动条设置为 k = 12，b = 0.5，m = 5000，v0 = 10。将 v 设置为 22.1，求出 t = 71.67，s = 1331.57。如下图所示：

点击图片打开网站可进入程序

根据计算，这道高考题数据有问题！在 72 s 内汽车无法达到 24 m/s，只有 21.85 m/s。如果要改进的话，可以将时间设置得长一些，例如当 t = 209.4 s 时，速度能达到 23.9 m/s，此时位移为 4554.36 m。

例 2

一道约 15 年前的老题：

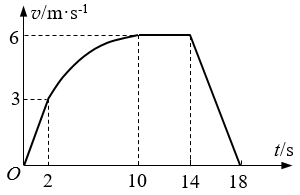某兴趣小组对一辆自制遥控小车的性能进行研究，他们让这辆小车在水平的直轨道上由静止开始运动，并将小车运动的全过程记录下来，通过处理转化为 v – t 图象，如图所示（除 2 s ~ 10 s 时间段图象为曲线外，其余时间段图像均为直线）。已知在小车运动的过程中，2 s ~ 14 s 时间段内小车的功率保持不变，在 14 s 末停止遥控而让小车自由滑行，小车的质量为 1.0 kg，可认为在整个运动过程中小车所受到的阻力大小不变。求：

（1）小车所受到的阻力；

（2）小车匀速行驶阶段的功率；

（3）小车在加速运动过程中（指图象中 0 ~ 10 秒内）位移的大小。

参考答案：（1）f = − 1.5 N          （2）P = 9 W         （3）s = 42 m

【分析】

这里关注的是第（3）小问，在 2 ~ 10 s 内小车做加速度不断减小的加速运动，在 8 s 内速度由 3 m/s 变为 6 m/s，通过的位移为 39 m。解题过程如下：

2 s ~ 10 s 内根据动能定理：Pt – fs₂ = \(\frac{1}{2}\) mv₂² − \(\frac{1}{2}\)mv₁²

解得 s₂ = 39 m

【验证】

此题中 k = \(\frac{P}{m}\)  = 9，b = \(\frac{f}{m}\) = 1.5，v₀ = 3 m/s，在 Geogebra 程序中进行验证，结果是：在 t = 8 s 内位移 s = 40.01 m，速度只达到 5.74 m/s，并没有接近 6 m/s。所以此题给出的数据有问题。

例 3

这是一道 20 年的老题。

电动机通过一质量不计的绳吊起质量为 8 kg 的物体，绳能承受的最大拉力为 120 N，电动机的输出功率可调整，最大输出功率为 1 200 W。要将此物体由静止起用最快的方式上升 90 m（己知此物体在吊高达到 90 m 时正好开始以最大速度匀速上升），求：（g 取 10 m/s²）

（1）物体上升过程中第一阶段加速度的大小和第一阶段末速度的大小；

（2）物体上升过程中的最大速度；

（3）物体上升所需最短时间。

参考答案：（1）a = 5 m/s²，v₁ = 10 m/s      （2）v_m = 15 m/s   （3）t_min = 7.75 s

【分析】

关注第（3）小问，原题的解答是：

设第二阶段所用时间为 t₂，物体上升的位移为 h₂ = H – h₁ = 90 m – 10 m = 80 m。由动能定理可得

P_mt₂ – mgh₂ = \(\frac{1}{2}\) mv₂² − \(\frac{1}{2}\) mv₁²

t₂ = \(\frac{{\frac{1}{2}mv_2^2 - \frac{1}{2}mv_1^2 + mg{h_2}}}{{{P_m}}}\)

代入数据后可解得 t₂ = 5.75 s。即在恒功率阶段物体以初速 v₁ = 10 m/s 运动，在 5.75 s 内上升 80 m，速度达到了 15 m/s。

【验证】

此题中 k = \(\frac{P}{m}\) = 150，b = \(\frac{f}{m}\) = 10，v₀ = 10 m/s，在 Geogebra 程序中进行验证，结果是：在 5.75 s 内上升了 80.09 m，速度达到了 14.92 m/s。此题的数据可以认为是正确的。

发布时间：2023/2/6 下午10:43:40  阅读次数：1644