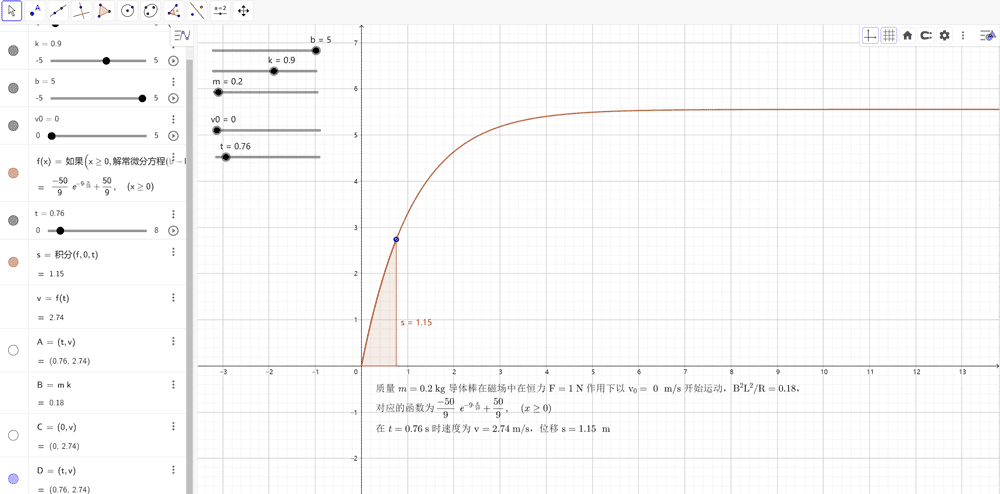
使用 Geogebra 解常微分方程

在高中阶段，变加速直线运动的分析是一个难点，限于高中数学知识的局限，很多问题往往只能定性分析，要定量计算，往往要涉及常微分方程的求解。

1、电磁感应中恒力作用下物体做切割磁感线运动的分析

此类问题在高中物理中很常见，我们可以通过受力平衡求解收尾速度、利用法拉第电磁感应定律求电量、动能定理求产生的电能和内能等。

例 1

此题为 2011 年上海高考题：

电阻可忽略的光滑平行金属导轨长 s = 1.15 m，两导轨间距 L = 0.75 m，导轨倾角为 30°，导轨上端 ab 接一阻值 R = 1.5 Ω 的电阻，磁感应强度 B = 0.8 T 的匀强磁场垂直轨道平面向上。阻值 r = 0.5 Ω，质量 m = 0.2 kg 的金属棒与轨道垂直且接触良好，从轨道上端 ab 处由静止开始下滑至底端，在此过程中金属棒产生的焦耳热 Q_r = 0.1 J。（取 g = 10m/s²）求：

（1）金属棒在此过程中克服安培力的功 W_安；

（2）金属棒下滑速度 v = 2 m/s 时的加速度 a；

（3）为求金属棒下滑的最大速度 v_m，有同学解答如下：由动能定理 W_重 − W_安 = \(\frac{1}{2}\)mv_m²，……。由此所得结果是否正确？若正确，说明理由并完成本小题；若不正确，给出正确的解答。

【参考答案】（1）W_安 = 0.4 J              （2）a = 3.2 m/s²           （3）v_m =  2.74 m/s

【分析】

这里关注的是第（3）小问，最大速度 v_m 的答案为 2.74 m/s。限于高中生的知识局限，只能用动能定理解决。

W_安 = Q = Q_R + Q_r = 0.4 J

mgssin30° − Q = \(\frac{1}{2}\)mv_m²

v_m = \(\sqrt {2gs\sin 30^\circ  - \frac{{2Q}}{m}} \) = \(\sqrt {2 \times 10 \times 1.15 \times 0.5 - \frac{{2 \times 0.4}}{{0.2}}} \) m/s = 2.74 m/s

【微积分解法】

如果运用微积分知识是可以直接求得速度大小的。

若只需求得 s 与 v 的函数关系，解法如下：

由牛顿第二定律可知：

mgsinθ − \(\frac{{{B^2}{L^2}v}}{{R + r}}\) = ma

代入数据可得 v 和 a 的关系式：

a = 5 − 0.9v

对应的微分方程为：

\[\frac{{\frac{{{\rm{d}}s}}{{{\rm{d}}t}}}}{{\frac{{{\rm{d}}v}}{{{\rm{d}}t}}}} = \frac{{{\rm{d}}s}}{{{\rm{d}}v}} = \frac{v}{a} = \frac{v}{{5 - 0.9v}}\]

使用分离变量法解此方程：

ds = \(\frac{v}{{5 - 0.9v}}\) dv，初始条件为 s|_{v = 0} = 0

s = \(\frac{1}{0.81}\)（− 0.9v − 5ln（− 0.9v + 5）+ 5ln5）

将 s = 1.15 m 代入以上函数可解得：v = 2.74 m/s。

若还需要求时间 t，可以写出以下微分方程

\(\frac{{{\rm{d}}v}}{{{\rm{d}}t}}\) = a = 5 − 0.9v，v|_{t = 0} = 0

解得

t = \(\frac{10}{9}\) [ln5 − ln(−0.9v + 5)]

或

v ＝ \(\frac{50}{9}\)（1 − e^−0.9t）

将 v = 2.74 m/s 代入以上函数，可求得 t = 0.75515 s。

进一步利用以下微分方程，还可以求出 s 与 t 的函数关系：

\(\frac{{{\rm{d}}s}}{{{\rm{d}}t}}\) = v = \(\frac{50}{9}\)（1 − e^−0.9t），s|_{t = 0} = 0

解得

s = \(\frac{{450t + 500{e^{ - 0.9t}} - 500}}{{81}}\)

将 s = 1.15 m 代入以上函数，可求得 t = 0.75484 s。数据是自洽的。

以上方程的求解很费时间，我翻出《高等数学》课本，花了老半天才解出结果。

2、使用 Geogebra 解常微分方程

在 Geogebra 中内置了解常微分方程的指令“解常微分方程[<fʹ(x,y)>]”，可以用来解 \(\frac{{{\rm{d}}y}}{{{\rm{d}}x}}\) = fʹ(x,y) 的解。

以上题为例，v 和 a 的关系式为：

a = 5 − 0.9v

对应的常微分方程为：

\(\frac{{{\rm{d}}v}}{{{\rm{d}}t}}\) = a = 5 − 0.9v，v|_{t = 0} = 0

5 − 0.9v 为一线性函数，令 k = 0.9，b = 5，v₀ = 0，这样就可以在 Geogebra 中动态设置这些变量，解决其他类似的问题。关键步骤如下：

1、设置对应 k、b、v₀ 变量的滑动条，设置表示时间 t 的滑动条；

2、输入 “f(x) = 解常微分方程(b – ky,(0,v0))”，这样就能绘制出 v – t 图像，并显示求解结果 “f(x) ＝− \(\frac{50}{9}\) e^−0.9t + \(\frac{50}{9}\)”，这个结果与前面解析求解的结果是相同的。

3、输入 “s = 积分(f,0,t)”，这样就可以通过 v – t 图像面积求出对应位移。

如下图所示，令滑动条 b = 5，k = 0.9，v0 = 0，将时间 t 拉至 0.755，对应的速度 v = 2.74 m/s，位移 s = 1.15 m。这个结果与前面解析求解的结果也是相同的。

点击图片可打开链接观看动态演示

3、使用 Geogebra 快速验证相关问题

有了上述工具，就可以验证一下其他题目了。

先说结论：在电磁感应中求解变加速运动过程中的能量、电量，若出现具体数字，一定要检查数据是否自洽，而不是为了计算简便凑数据。

例 2

此题是约 20 年前的一道老题：

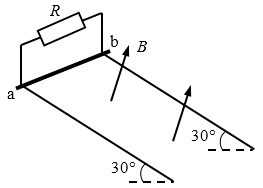光滑平行金属导轨长 L = 2 m，二导轨间距 d = 0.5 m，轨道平面与水平面的夹角为 θ = 30°，导轨上端接一阻值为 R = 0.5 Ω 的电阻，其余电阻不计，轨道所在空间有垂直轨道平面的匀强磁场，磁感应强度 B = 1 T。有一不计电阻的金属棒 ab 的质量 m = 0.5 kg，放在导轨最上端，如图所示。当 ab 棒从最上端由静止开始自由下滑，到达底端脱离轨道时，电阻 R 上产生的热量为 Q = 1 J，求：

（1）当棒的速度为 v = 2 m/s 时，它的加速度是多少？

（2）棒下滑的最大速度是多少？

（3）棒下滑过程中通过电阻 R 的最大电流是多少？

【参考解答】（1）a = 3 m/s²        （2）v_m = 4 m/s      （3）I_m = 4 A

【验证】

由牛顿第二定律得：mgsin30° − \(\frac{{{B^2}{L^2}v}}{{R}}\) = ma

代入数据可得 v 和 a 的关系式：a = 5 – v

在 Geogebra 程序中将设置 b = 5，k = 1，v0 = 0，结果是“到达底端位移为 2 m，用时 t = 1.05 s，速度为 v = 3.25 m/s，而不是参考答案中的 4 m/s”。错误的原因是 Q = 1 J 这个数据不自洽，导致此题（2）（3）都是错误的。

例 3

此题是一道约 15 年前的老题：

如图甲所示，MN、PQ 为间距 L = 0.5 m 足够长的平行导轨，NQ⊥MN，导轨的电阻均不计。导轨平面与水平面间的夹角 θ = 37°，NQ 间连接有一个 R = 4 Ω 的电阻。有一匀强磁场垂直于导轨平面且方向向上，磁感应强度为 B₀ = 1 T。将一根质量为 m = 0.05 kg 的金属棒 ab 紧靠 NQ 放置在导轨上，且与导轨接触良好。现由静止释放金属棒，当金属棒滑行至 cd 处时达到稳定速度，已知在此过程中通过金属棒截面的电量 q = 0.2 C，且金属棒的加速度 a 与速度 v 的关系如图乙所示，设金属棒沿导轨向下运动过程中始终与 NQ 平行。（取 g = 10 m/s²，sin37° = 0.6，cos37° = 0.8）。求：

（1）金属棒与导轨间的动摩擦因数 μ；

（2）cd 离 NQ 的距离 s；

（3）金属棒滑行至 cd 处的过程中，电阻 R 上产生的热量。

【参考解答】（1）μ =  0.5  （2）s = 2 m  （3）Q_R =  0.08 J

【验证】

图像已经直接给出了 v 和 a 的关系式：a = 2 – v

在 Geogebra 程序中将设置 b = 2，k = 1，v0 = 0，结果是“当速度 v ≈ 2 m/s 时，用时 t ≈ 6 s，位移 s ≈ 10 m，而不是参考答案中的 2 m”。错误的原因是电量 q = 0.2 C 这个数据不自洽，导致此题（2）（3）都是错误的。

如何求达到稳定速度时的位移 s？过程如下：

由 a = 2 – v

得  \(\frac{{{\rm{d}}s}}{{{\rm{d}}v}} = \frac{v}{a} = \frac{v}{{2 - v}}\)

使用分离变量法解此方程：ds = \(\frac{v}{{2 - v}}\) dv，初始条件为 s|_{v = 0} = 0，解得：

s =− v − 2ln（− v + 2）+ 2ln2

将 v = 2 m/s 代入上式，出现 ln0 无解！那是因为根据对应的速度时间函数 v = −2e^−t + 2（过程略），理论上需要经过无穷大的时间才能达到稳定速度，对应的位移也是无穷大。

若将 v = 1.9 m/s 代入上述方程可解得 s =  4.09 m，速度为 1.99 m/s 时位移达到 8.61 m，速度为 1.999 m/s 时位移为 13.2 m……。那么前面为什么求出“当速度 v ≈ 2 m/s 时，用时 t ≈ 6 s，位移 s ≈ 10 m”呢？应该是程序中的小数点太多不显示的缘故，可能对应的速度只有 1.995…… m/s。

所以关于“多久、多远能达到稳定速度？”是高中物理中一个比较头疼的问题，我们通常可以像例 1、例 4 那样回避稳定速度，或者以文字题的形式回避数值的运算。

例 4

此题是 2021 年河北高考模拟题：

如图 1 所示，两条足够长的平行金属导轨间距为 0.5 m，固定在倾角为 37° 的斜面上。导轨顶端连接一个阻值为 1 Ω 的电阻。在 MN 下方存在方向垂直于斜面向上、大小为 1 T 的匀强磁场。质量为 0.5 kg 的金属棒从 AB 处由静止开始沿导轨下滑，其运动过程中的 v – t 图象如图 2 所示。金属棒运动过程中与导轨保持垂直且接触良好，不计金属棒和导轨的电阻，取 g = 10 m/s²，sin37° = 0.6，cos37° = 0.8。

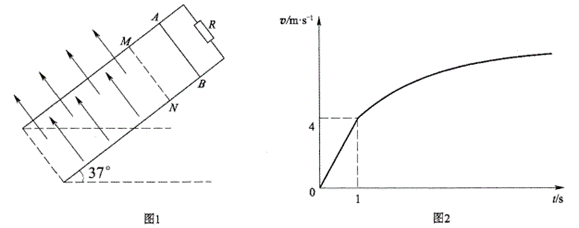
（1）求金属棒与导轨间的动摩擦因数；

（2）求金属棒在磁场中能够达到的最大速率；

（3）已知金属棒从进入磁场到速度达到 5 m/s 时通过电阻的电荷量为 1.3 C，求此过程中电阻产生的焦耳热。

【参考解答】（1）0.25         （2）8 m/s              （3）2.95 J

【验证】

v 和 a 的关系式：a = 4 – 0.5v

在 Geogebra 程序中将设置 b = 4，k = 0.5，v0 = 4，结果是“当速度 v = 5 m/s 时，位移 s = 2.6 m”，数据是自洽的。

4、电磁感应中恒功率作用下物体做切割磁感线运动的分析

例 5

也是一道近 20 年前的老题了：

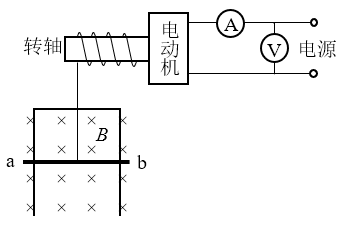如图所示，电动机通过其转轴上的绝缘细绳竖直向上牵引一根原来静止的长为 L = 1 m、质量 m = 0.1 kg导体棒 ab，导体棒紧贴在竖直放置、电阻不计的金属框架上，导体棒的电阻 R = 1 Ω，磁感强度 B = 1 T 的匀强磁场方向垂直于导体框架所在平面，当导体棒在电动机牵引下上升 h = 3.8 m 时，获得稳定速度，此过程导体棒产生热量 Q = 2 J。电动机工作时，输出功率 P = 6 W 恒定，不计一切摩擦，求：

（1）导体棒所达到的稳定速度是多少？

（2）导体棒从静止到达稳定速度的时间是多少？

【验证】

第（1）小题的参考答案 v = 2 m/s，第（2）题的参考答案 t = 1 s。但是，就算棒以最大速度 2 m/s 运动，在 1 s 内的位移只有 2 m，小于题中 h = 3.8 m。错误的原因是 h 这个数据不自洽。

【微积分求解】

此题中 v 和 a 的关系式：a = \(\frac{{{\rm{d}}v}}{{{\rm{d}}t}}\) = \(\frac{{60}}{v}\) – 10v – 10，解这个方程，先分离变量：

\[\frac{{{\rm{d}}v}}{{\frac{{60}}{v} - 10v - 10}} = {\rm{d}}t\]

\[ - \frac{v}{{10{v^2} + 10v - 60}}{\rm{d}}v = {\rm{d}}t\]

然后查《高等数学》书后的积分表

\[\int {\frac{x}{{a{x^2} + bx + c}}dx}  = \frac{1}{{2a}}\ln \left| {a{x^2} + bx + c} \right| - \frac{b}{{2a}}\int {\frac{dx}{{a{x^2} + bx + c}}} \]

而

\[\int {\frac{{dx}}{{a{x^2} + bx + c}}}  = \left\{ {\begin{array}{*{20}{c}}{\frac{2}{{\sqrt {4ac - {b^2}} }}\arctan \frac{{2ax + b}}{{\sqrt {4ac - {b^2}} }} + C{\rm{    }}\;\;\;\;\;({b^2} < 4ac)}\\{\frac{1}{{\sqrt {{b^2} - 4ac} }}\ln \left| {\frac{{2ax + b - \sqrt {{b^2} - 4ac} }}{{2ax + b + \sqrt {{b^2} - 4ac} }}} \right| + C{\rm{   }}\;\;\;\;({b^2} > 4ac)}\end{array}} \right.\]

因此取 a = 10、b = 10、c = − 60，初始条件为 t | _{v = 0} = 0。解得：

t = − \(\frac{1}{20}\) ln| 10v² + 10v – 60 | + \(\frac{1}{100}\) ln \(\left| {\frac{{20v - 40}}{{20v + 60}}} \right|\) + \(\frac{1}{20}\) ln 60 − \(\frac{1}{100}\) ln \(\frac{2}{3}\)

= − \(\frac{3}{50}\) ln(v + 3) − \(\frac{1}{20}\) ln(2 − v) + \(\frac{3}{50}\) ln 3 + \(\frac{1}{25}\) ln 2

v 是取不到 2 的，方程无解，若取 t = 1 s，速度 v 能达到 1.9999999999 m/s，上升高度 h 约为 1.9532 m。可见，在恒功率情况下，物体可以在很短时间内接近收尾速度。

那么让 Geogebra 帮忙呢？输入函数，显示“？”，它也不会解？！原因是：虽然我们已经得到了 t – v 函数，但是它的反函数 v – t 没有可以用初等函数表示的解析解。

发布时间：2023/2/3 下午2:40:06  阅读次数：4466