第 2 节  法拉第电磁感应定律  教学建议

1．教学目标

（1）通过实验，理解法拉第电磁感应定律。知道 E = Blvsinθ 是法拉第电磁感应定律的一种特殊形式，会用法拉第电磁感应定律在具体情境中分析求解有关问题。

（2）经历分析推理得出法拉第电磁感应定律的过程，体会用变化率定义物理量的方法；经历推理得出 E = Blvsinθ 的过程，体会矢量分解的方法。

（3）知道 E = \(\frac{{\Delta \Phi }}{{\Delta t}}\) 与 E = Blvsinθ 的内在联系，感悟事物的共性与个性的关系，体会辩证唯物主义的方法和观点。

2．教材分析与教学建议

前面几节的内容是从感应电流的角度来认识电磁感应现象的。本节是从感应电流进一步深入剑感应电动势来理解的，即研究“决定感应电动势大小的因素”。

本节非常重视概念建构过程，通过对一个个问题情境的探究总结归纳出物理规律，体现对学生核心素养培养的要求。首先，通过创设问题情境，让学生思考和讨论，在问题的探讨中逐步形成物理概念；其次，通过定性实验对问题进一步深入探究，意在培养学生的科学探究能力；随后，以陈述事实的方式引入法拉第电磁感应定律，由于法拉第电磁感应定律很难通过定量实验来探究，教材中并没有做要求，而是陈述客观事实，解释了为什么要命名为法拉第电磁感应定律，体现科学态度与责任；最后，用法拉第电磁感应定律推导出导体切割磁感线的感应电动势公式，重视对学生科学思维的培养。很多物理规律的得出，要经历对事实经验的思考，定性或定量实验的探究，对实验结果和大量经验的总结和归纳，最终得到比较完备的物理规律，让学生体验和经历这样的建构过程，有助于学生科学素养的提高。

同时，教材还关注了电磁感应现象中能量转化的过程，让学生从能量守恒的角度理解电磁感应现象，对学生能量观的形成很有好处，教师在进行这一部分的教学时应予以适当关注。

本节教学的重点是法拉第电磁感应定律，难点是对磁通量的变化及磁通量的变化率的理解。

（1）问题引入

教师通过演示实验创设问题情境，让学生思考和讨论，引导学生说出影响感应电流大小的因素有哪些，学生通过讨论和教师的引导认识到感应电流的大小与磁通量的变化率有关：磁通量的变化率越大，感应电流越大。也可以引导学生回顾插入线圈产生感应电流的实验，实验中的磁性越强，插入的速度越大，产生的感应电流越大。教师还可以通过“做一做”栏目或一些其他的例子，使学生意识到：当电路中的电阻一定时，感应电流的大小与磁通量的变化快慢有关，而磁通量的变化快慢可以用磁通量的变化率来描述（类比于速度的变化率），那么感应电流的大小就与磁通量的变化率有关，从而让学生财影响感应电流大小的因素有一个初步的认识。

（2）感应电动势

引入感应电动势的概念，要注意温故知新。闭合电路中要维持持续电流，其中必有电动势的存在。在电磁感应现象中，闭合电路中有感应电流，必然存在对应的电动势，即感应电动势。

比较概念之间的内在联系，使学生深刻理解概念的本质。由感应电流过渡到感应电动势，对学生来说，是从现象到本质的认识深化过程。为了让学生认识到感应电流与感应电动势的区别和联系，教师可以通过演示实验，让学生观察接通与断开闭合电路时的电流与路端电压。即当电路断开时，电路中没有感应电流，但路端电压（即感应电动势）仍然存在。而电路中出现感应电流，要同时满足电路闭合与电动势存在这两个前提条件。所以，感应电动势的有无，完全决定于磁通量是否发生变化，与电路的通断、电路的组成情况等无关。在电磁感应现象中，“感应电动势”比“感应电流”更具有本质意义。

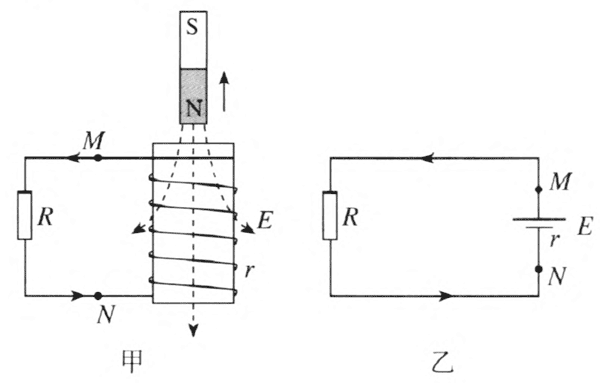
结合实例进行对比分析，对巩固和深化概念很有效。如图 2–2 甲所示，电路中的线圈相当于电源，其电动势为感应电动势，线圈导线的电阻相当于电源内阻，进而可画出如图 2–2 乙所示的电路图，以便学生类比掌习。

建立感应电动势概念的教学思路可以归纳为：电磁感应现象→感应电流→电源→感应电动势。

（3）法拉第电磁感应定律

教学设计的思路如下：

按上述线索进行教学时，一是要使学生对演示实验的现象观察清楚；二是要结合实验、实例，运用类比等方法，加深学生对磁通量变化率概念的理解。教学中，可以列举速度由位置的变化率决定，加速度由速度的变化率决定等事例，以此来加深对变化率概念的理解。

 

教学片段

影响感应电动势大小的因素

观察教材图 2.2–1 所示的实验，分析、思考并回答下面的问题。

问题：将强磁体自由释放，如教材图 2.2–1 所示穿过线圈，电压表指针发生偏转。其原因是什么？电压表的示数代表什么？

分析：磁体周围存在磁场，穿过线圈的过程中线圈的磁通量发生变化，从而产生感应电动势。电压表接在线圈的两端，便可以测出线圈两端的感应电动势，从而直接研究影响感应电动势大小的因素。

问题：同样的磁体、同样的线圈匝数，从不同高度释放穿过线圈，有什么相同和不同？

分析：同样的磁体、同样的线圈匝数，磁体穿过线圈的过程中线圈磁通量的变化量是相同的，但是磁体穿过的时间不同，从而磁通量的变化快慢不同，即磁通量的变化率不同。

问题：同样的线圈匣数、从同样的高度释放磁性强弱不同的磁体，磁体穿过线圈，有什么相同和不同？

分析：释放高度相同，磁体穿过线圈的时间是相同的，但是磁体的磁性强弱不同，磁感应强度不同，那么磁通量的变化不同，从而磁通量的变化率也就不同。

问题：同样的磁体从同样的高度释放，不同线圈匝数，有什么相同和不同？

分析：同样的磁体、释放高度相同，磁通量的变化率相同，但线圈是由 n 个单匝线圈串联而成的，因此整个线圈中的感应电动势是单匝的 n 倍。

分析归纳：设计表格，记录实验数据，之后归纳总结出感应电动势与哪些因素有关。综合考虑表格中的各个因素，可以初步得到感应电动势的大小与线圈匝数正相关，与磁通量的变化率正相关。

（4）法拉第电磁感应定律的表达式

推导法拉第电磁感应定律表达式的思路如下：

教学中还应注意以下儿点：

①讲清比例常数是 k，可引导学生推导 1 Wb/s 与 1 V 的关系，从而得出 k = 1 的结论，因此法拉第电磁感应定律的表达式为 E = \(\frac{{\Delta \Phi }}{{\Delta t}}\)。

②要使学生了解如果闭合电路由 n 匝线圈串联组成，整个线圈总的感应电动势是单个线圈的 n 倍，即 E = n \(\frac{{\Delta \Phi }}{{\Delta t}}\)。这里要说明，穿过每匝线圈的磁通量的变化率是相同的。

（5）理解法拉第电磁感应定律

为加深学生对法拉第电磁感应定律的理解，可以适当增加例题。例题的选择与分析，特别要注意纠正学生可能存在的误解，区别 Φ、ΔΦ 与 \(\frac{{\Delta \Phi }}{{\Delta t}}\)。

磁通量是状态量，反映的是某一时刻穿过回路磁通量的大小；ΔΦ 是穿过回路磁通量的变化，是过程量，反映的是某一段时间穿过回路磁通量的变化的大小；\(\frac{{\Delta \Phi }}{{\Delta t}}\) 是穿过回路磁通量的变化率，其数值与 ΔΦ 及所用时间 Δt 都有关系，\(\frac{{\Delta \Phi }}{{\Delta t}}\) 是 Φ–t 图像上某点切线的斜率。

因此，Φ 大，ΔΦ 不一定大；ΔΦ 大，\(\frac{{\Delta \Phi }}{{\Delta t}}\) 也不一定大，三者没有直接的数量关系。它们是三个不同的物理量。Φ、ΔΦ 与 \(\frac{{\Delta \Phi }}{{\Delta t}}\) 三者的关系，可以用 v、Δv 与 \(\frac{{\Delta v }}{{\Delta t}}\) 三者的关系来类比。

教材在这里特地介绍了磁通量的变化率，目的是为学生准确理解法拉第电磁感应定律扫清障碍。另外，需要注意，教材中给出的法拉第电磁感应定律公式中的 ΔΦ 取绝对值，\(\frac{{\Delta \Phi }}{{\Delta t}}\) 也取绝对值，它表示的是感应电动势的大小，而不涉及方向。

（6）导线切割磁感线时的感应电动势

引起闭合电路磁通量变化的原因有多种，例如，闭合电路的一部分导体在磁场中切割磁感线运动时，会引起磁通量的变化。利用 E = n \(\frac{{\Delta \Phi }}{{\Delta t}}\) 来研究导体切割磁感线运动，可推导出感应电动势的公式为 E = Blvsinθ，注意条件是 v 与 l 垂直，其中 θ 是 B 和 v 的夹角。

不论从分解速度的角度还是从分解磁感应强度的角度来理解这个公式，其意义是等价的。因为不论把 B 分解为 B_∥ 和 B_⊥，还是把 v 分解为 v_∥ 和 v_⊥，都会得出相同的结果。

E = Blvsinθ 是一个重要的公式。要使学生了解它是法拉第电磁感应定律的一个特例，当研究导体做切割磁感线运动的有关问题时，使用它比较方便。

教学中，要让学生注意公式 E = \(\frac{{\Delta \Phi }}{{\Delta t}}\) 与 E = Blvsinθ 在以下几个方面的区别及联系。

研究对象不同。E = \(\frac{{\Delta \Phi }}{{\Delta t}}\) 的研究对象是一个回路，而 E = Blvsinθ 的研究对象是磁场中运动的一段导体。

②E = \(\frac{{\Delta \Phi }}{{\Delta t}}\) 表示的电动势是整个回的感应电动势，而不是回路中某部分导体的电动势。整个回路的电动势为 0，其回路中某段导体的感应电动势不一定为 0。

③E = \(\frac{{\Delta \Phi }}{{\Delta t}}\) 和 E = Blvsinθ 本质上是统一的。当导体做切割磁感线运动时，用 E = Blvsinθ 求 E 比较方便；当穿过电路的磁通量发生变化时，用 E = \(\frac{{\Delta \Phi }}{{\Delta t}}\) 求 E 比较方便。

（7）电磁感应现象中的洛伦兹力

教材对这一内容的呈现是通过“思考和讨论”栏目来引导的，通过分析导体切割磁感线这一特例中的力学特征来理解动生电动势的产生。这一内容的关键是要引导学生从宏观的导体棒的分析深入到微观的自由电荷的受力分析，不仪要关注洛伦兹力作用下自由电荷的运动、积累从而形成电势差，还要关注导体棒运动过程中能量的转化过程。教师在教学中应该通过层层引导，使学生对导体棒切割磁感线运动这一过程的本质认识逐步清晰，理解逐步透彻。

 

教学片段

导体切割磁感线运动过程中的动力学和能量特征

引导学生分析教材图 2.2–4 中的过程，提出从下问题让学生思考、讨论，最后教师再总结归纳形成观点。

问题：图中导体棒中的自由电荷（可以认为是正电荷）随着导体棒运动受到的洛伦兹力向哪个方向？自由电荷如何运动？

（这一问题意在引导学生从微观角度理解这一过程，认识感生电动势产生的原因。）

问题：导体棒一直运动下去，自由电荷是否一直沿着导体棒运动？为什么？导体棒哪一端电势比较高？

（这一问题意在引导学生理解感生电动势是如何产生的。）

问题：如果没有外力，导体棒将如何运动？能量是如何转化的？

（这一问题意在引导学生从能量守恒的角度进一步认识导体切割磁感线的过程。）

3．“练习与应用”参考答案与提示

本节共 6 道习题。第 1 题是对法拉第电磁感应定律的直接考查。第 2、3 题都是对导体切割磁感线的考查，其中第 2 题需要建立模型进行相关定量计算，第 3 题需要对线圈切割均匀轴向磁场磁感线的情境进行定性分析，培养学生处理实际问题的能力。第 4 题的目的是使学生掌握，线圈在匀强磁场中绕垂直于磁场方向的轴匀速转动切割磁感线产生感应电动势的最大值，同时为学习交变电流的产生奠定基础。第 5 题通过对电磁流量计的分析，提高学生应用电磁感应现象解决实际问题的能力。第 6 题的目的是使学生掌握导体棒绕其端点匀速转动，垂直切割磁感线时产生的感应电动势。

 

1．175 V，0.175 A

提示：根据法拉第电磁感应定律，线圈中产生的感应电动势

E = n \(\frac{{\Delta \Phi }}{{\Delta t}}\) = 1 000×\(\frac{{0.09 - 0.02}}{{0.4}}\) V = 175 V

根据闭合电路欧姆定律，通过电热器的电流

I = \(\frac{E}{{R + r}}\) = \(\frac{{175}}{{990 + 10}}\) A = 0.175 A

 

2．7.2×10³ V

提示：缆绳切割磁感线产生感应电动势

E = BLv = 4.6×10⁻⁵×20.5×10³×7.6×10³ = 7.2×10³ V

 

3．可以当作话筒。我们对着纸盆说话，声音使纸盆振动，线圈随着纸盆振动，切割磁感线产生感应电流。

 

4．线圈绕 OOʹ 轴匀速转动时，竖直边 l₂ 切割磁感线，由于速度方向不断变化，所以感应电动势发生变化。在图示位置时，由 E = Bl₂vsinθ 和 v = ωl₁ 得 E = Bl₂1₁ωsinθ。又因 S = l₁l₂，θ = 90°，所以 E = BSω。

 

5．Q = \(\frac{{\pi d}}{{4B}}\) U

提示：管中有导电液体流过时，相当于一段长为 d 的导体在切割磁感线，M、N 两点间电势差的大小等于产生的感应电动势，U = E = Bdv。液体的流量 Q = vπ（\(\frac{d}{2}\)）²，即液体的流量 Q 与电动势 E 的关系为 Q = \(\frac{{\pi d}}{{4B}}\) U。

 

6．E = \(\frac{1}{2}\) Bl²ω

提示：方法一：由法拉第电磁感应定律 E = n \(\frac{{\Delta \Phi }}{{\Delta t}}\)，导体棒转动 Δt 时间转过的角度 θ = ωΔt，扫过的扇形画积为 S = \(\frac{\theta }{{2\pi }}\)πl²，则 ab 两端产生的感应电动势大小 E = Bl²ω。

方法二：利用公式 E = Blv，导体棒绕其端点转动时，各点的平均速度 v = \(\frac{{\omega l}}{2}\)，所以产生的感应电动势大小 E = \(\frac{1}{2}\) Bl²ω。