复习与提高参考答案与提示

本章主要围绕静电场的基础知识设置习题，在覆盖了本章所有重、难点的情况下，还涉及物理思维方法和数学工具的应用，因此某些题目对学生思维能力和计算能力要求较高。

A 组

1．当验电器带电时，两片金属箔上带同种电荷，同种电荷相互排斥，所以两片金属箔会张开一定的角度。当金属箔受力平衡时，就能保持静止状态，其张角就不会再增大。

 

2．若先将 A、B 分开，再移走 C，则 A 带负电、B 带正电；若先将 C 移走，再把A、B 分开，则 A、B 均不带电。

 

3．虽然 A、B 两球所带的电荷量不同，但它们之间相互作用的静电力的大小相等。A、B 两球质量相等，所受重力相同。根据对称性可断定 α = β。

 

4．第三个小球应放在 Q 和 9Q 之间的连线上，且距 Q 0.1 m 处；带负电荷；电荷量是 Q 的 \(\frac{9}{{16}}\)。

提示：要使三个小球都处于平衡状态，每个小球所受另外两个小球的静电力应彼此平衡，而原来的 Q 和 9Q 是互相排斥的，由此可以判断第三个小球应带负电荷，并要放在 Q 和 9Q 的连线上，位于 Q 和 9Q 中间的某一位置。设第三个小球的电荷量为 Q_x（取绝对值），与 Q 的距离为 x，Q 与 9Q 间的距离为 l（1 = 0.4 m），受力情况如图 9–12 所示。

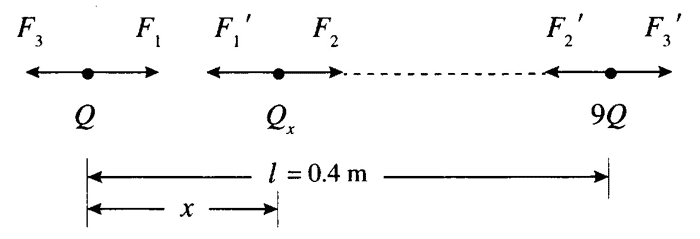
设 Q 与 Q_x 间的相互作用力为 F₁ 和 F₁ʹ，有 F₁ = F₁ʹ = k\(\frac{{Q{Q_x}}}{{{x^2}}}\)。设 9Q 与 Q_x 间的相互作用力为 F₂ 和 F₂ʹ，有 F₂ = F₂ʹ = k\(\frac{{9Q{Q_x}}}{{{{(l - x)}^2}}}\)。设 Q 与 9Q 间的相互作用力为 F₃ 和 F₃ʹ，有 F₃ = F₃ʹ = k\(\frac{{9{Q^2}}}{{{l^2}}}\)。由 F₁ = F₃ 可得 k\(\frac{{Q{Q_x}}}{{{x^2}}}\) = k\(\frac{{9{Q^2}}}{{{l^2}}}\)，由 F₂ʹ = F₃ʹ 可得 k\(\frac{{9Q{Q_x}}}{{{{(l - x)}^2}}}\) = k\(\frac{{9{Q^2}}}{{{l^2}}}\)。解得 x = \(\frac{l}{{4}}\) = \(\frac{0.4}{{4}}\) m = 0.1 m，Q_x = 9Q（\(\frac{x}{{l}}\)）² = 9Q（\(\frac{0.1}{{0.4}}\)）² = \(\frac{9}{{16}}\)Q。

 

5．2.94×10⁻⁹ C

提示：带电小球在静电力 F、重力 mg 和绳的拉力 F_T 作用下平衡。由平衡条件可知 F = mg tanθ。其中 θ 为悬线偏离竖直方向的夹角，即 tan θ = \(\frac{{0.02}}{{2.0}}\) = 0.01。设小球所带电荷量为 q（负电荷），根据 F = qE 解得 q = \(\frac{{mg\tan \theta }}{E}\) = 2.94×10⁻⁹ C。

 

6．\(\frac{{kq}}{{{{\left( {R + \frac{l}{2}} \right)}^2}}}\)，方向向左

B 组

1．此现象并不是说明制造出了永动机，也没有违背能量守恒定律。因为，在把 A、B 分开的过程中要克服 A、B 之间的静电力做功。这是把机械能转化为电能的过程。

 

2．设两个金属球所带电荷量分别为 q₁ 和 q₂，则 q₁ + q₂ = Q 为一个定值。又由库仑定律 F = k\(\frac{{{q_1}{q_2}}}{{{r^2}}}\)，得 F = k\(\frac{{{q_1}(Q - {q_1})}}{{{r^2}}}\)。知当 q₁ = q₂ = \(\frac{Q}{{2}}\) 时，F 最大。

 

3．负，2\(\sqrt 2 \)q

提示：q′ 在 D 点产生的电场强度与 A、C 点的 q 共同在 D 点产生的电场强度大小相等、方向相反。设正方形边长为 L，有 k\(\frac{q}{{{L^2}}}\)×\(\sqrt 2 \) = k\(\frac{{q'}}{{{{(\sqrt 2 L)}^2}}}\)，得 q′ = 2(\sqrt 2 \)q ，带负电。

 

4．\(\frac{{kq}}{{{{(3d)}^2}}}\)，方向向左

提示：根据电场强度的叠加原理可知，薄板在 A 点产生的电场强度大小为 \(\frac{{kq}}{{{{(3d)}^2}}}\)，方向向右；再根据对称性可知，薄板在 B 点产生的电场强度大小也为 \(\frac{{kq}}{{{{(3d)}^2}}}\)，方向向左。

 

5．（1）\(\frac{{2kqQx}}{{{{\left[ {{x^2} + {{\left( {\frac{l}{2}} \right)}^2}} \right]}^{\frac{3}{2}}}}}\)

（2）\(\frac{{kqQl}}{{{{\left[ {{x^2} + {{\left( {\frac{l}{2}} \right)}^2}} \right]}^{\frac{3}{2}}}}}\)

（3）l > 2x

提示：设 AC 与 CO 的夹角，以及 BC 与 CO 的夹角均为 θ。

（1）由库仑定律和平衍四边形定则可得 F₁ =k\(\frac{{2qQ\cos \theta }}{{{x^2} + {{\left( {\frac{l}{2}} \right)}^2}}}\) = \(\frac{{2kqQx}}{{{{\left[ {{x^2} + {{\left( {\frac{l}{2}} \right)}^2}} \right]}^{\frac{3}{2}}}}}\)。

（2）由库仑定律和平行四边形定则可得 F₂ = k\(\frac{{2qQ\sin \theta }}{{{x^2} + {{\left( {\frac{l}{2}} \right)}^2}}}\) = \(\frac{{kqQl}}{{{{\left[ {{x^2} + {{\left( {\frac{l}{2}} \right)}^2}} \right]}^{\frac{3}{2}}}}}\)

（3）由前两问的结论可得 l > 2x。

 

6．（1）A 点和 B 点的电场强度大小分别为 40 N/ C和 2.5 N/C，方向均沿 x 轴正方向；

（2）0.2 m

提示：（1）由电场强度的定义式可得 E_A = \(\frac{{{F_a}}}{q}\) = 40 N/C，方向沿 x 轴正方向。E_B = \(\frac{{{F_b}}}{q}\) = 2.5 N/C，方向沿 x 轴正方向。

（2）由于点电荷在两点产生的电场强度方向相同，且 A 点电场强度大于 B 点电场强度，所以场源电荷必定在 A 点的左侧。设场源电荷的坐标为 x，E_A = k\(\frac{Q}{{{{(0.3 - x)}^2}}}\)，E_B = k\(\frac{Q}{{{{(0.6 - x)}^2}}}\)，解得 x = 0.2 m。