第三章 复习与提高
A 组
1.指出下列说法中的错误:
(1)因为物体本身就有重力,所以重力没有施力物体。
(2)重力的方向总是垂直于接触面向下的。
(3)放在水平桌面上的两个球,靠在一起但并不互相挤压,两球之间存在弹力。
(4)两物体间如果有相互作用的弹力,就一定存在摩擦力。
(5)根据 μ = \(\frac{{{F_\rm{f}}}}{{{F_\rm{N}}}}\) 可知,动摩擦因数 µ 跟滑动摩擦力 Ff 成正比,跟支持力 FN 成反比。
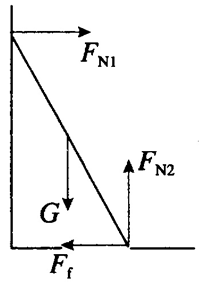
2.如图 3–1,一架直梯斜靠在光滑的竖直墙壁上,下端放在粗糙的水平地面上,直梯处于静止状态。请画出从侧面观察时直梯的受力示意图。
3.请设计一个测量纸跟桌面之间动摩擦因数的方法,画出示意图,说明测量方法,写出测量的计算式。
4.如图 3–2,两人用同样大小的力共提一
桶水,两人手臂间的夹角是大些省力,还是小些省力?请通过推导得出你的结论。
5.生活中经常用刀来劈开物体。图 3–3 是刀刃的横截面,F 是作用在刀背上的力,若刀刃的横截面是等腰三角形,刀刃两侧面的夹角为 θ,求刀劈物体时对物体侧向推力 FN 的大小。
6.如图 3–4,用一根轻质细绳将一幅重力
为 10 N 的画框对称悬挂在墙壁上,画框上两个挂钉间的距离为 0.5 m。已知绳能承受的最大拉力为 10 N,要使细绳不会被拉断,绳子最短要多长?
B 组
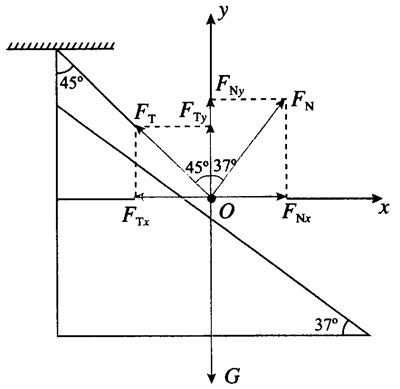
1.如图 3–5,光滑斜面上有一个重力为 100 N 的小球被轻绳拴住悬挂在天花板上,已知轻绳与竖直方向的夹角为 45°,斜面倾角为 37°,整个装置处于静止状态。求轻绳对小球拉力的大小和斜面对小球支持力的大小。(sin37° = 0.6)
2.一台空调外机用两个三角形支架固定在外墙上(图 3–6),空调外机的重心恰好在支架横梁和斜梁的连接点 O 的上方,重力大小为 200 N。横梁 AO 水平,斜梁 BO 跟横梁的夹角为 37°,sin 37° = 0.6。
(1)横梁对 O 点的拉力沿 OA 方向,斜梁对 O 点的压力沿 BO 方向,这两个力各有多大?
(2)如果把斜梁加长一点,仍保持连接点 O 的位置不变,横梁仍然水平,这时横梁和斜梁对 O 点的作用力大小将如何变化?
3.木块 A、B 分别重 50 N 和 60 N,它们与水平地面之间的动摩擦因数均为 0.25,夹在 A、B 之间的轻弹簧被压缩了 2 cm,弹簧的劲度系数为 400 N/m,系统置于水平地面上静止不动。现用 1 N 的水平拉力 F 作用在木块 B 上,如图 3–7 所示,求力 F 作用后木块 A、B 所受摩擦力的大小。
4.如图 3–8,重力为 G 的木块,恰好能沿倾角为 θ 的斜面匀速下滑,那么要将木块沿斜面匀速向上推,必须加多大的水平推力 F?
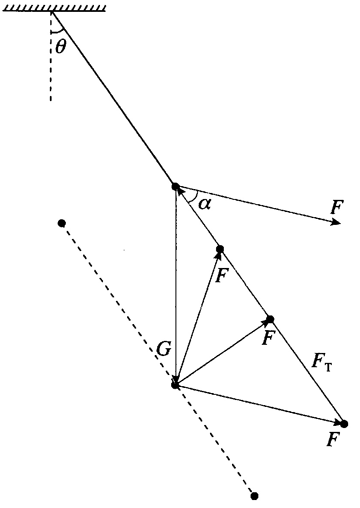
5.一根细线系着一个小球,细线上端固定在横梁上。给小球施加力 F,小球平衡后细线跟
竖直方向的夹角为 θ,如图 3–9 所示。现改变 F 的方向,但仍然要使小球在图中位置保持平衡,即保持 θ 不变,问:F 可能的方向有哪些?请在图中标明 F 方向的范围,并简述理由。以上 F 的大小可以任意调节。
6.用三根细线 a、b、c 将重力均为 G 的两个小球 1 和 2 连接并悬挂,如图 3–10 所示。两小球处于静止状态,细线 a 与竖直方向的夹角为 30°,细线 c 水平。求:
(1)求细线 a、c 分别对小球 1 和 2 的拉力大小;
(2)求细线 b 对小球 2 的拉力大小。
7.国际拔河比赛中每个队由 8 名运动员组成。比赛规定,每个队按 8 名运动员体重的总和分成若干重量级别,同等级别的两个队进行比赛。还规定,运动员必须穿“拔河鞋”或没有鞋跟等突出物的平底鞋,不能戴手套。
(1)竞赛为什么要作出上述规定?试从物理学的角度进行说明。
(2)专业的拔河运动员在拔河时身体向后倾倒,跟地面的夹角很小,为什么要这样做?请从物理原理上分析说明。
复习与提高参考答案与提示
A 组 6 道习题联系生活实际,通过复习关于重力、弹力、摩擦力、力的合成与分解、平衡力和相互作用力等物理基本概念和规律,形成正确的物理观念;通过在熟悉的问题情境中根据需要选用恰当的模型解决简单的物理问题;对问题进行分析,通过推理,获得结论,作出解释,并能恰当使用证据表达自己的观点。其中第 3 题还要求设计一个测量纸跟桌面之间动摩擦因数的方法,进行科学探究。
B 组 7 道习题要求运用本章所学的力学知识对综合性物理问题进行分析和推理,获得正确结论并作出解释,能将较复杂的实际问题中的对象和过程转换成物理模型,面对真实情境从不同角度提出并准确表述可探究的物理问题。
A 组
1.(1)任何一个力都有施力物体和受力物体。重力也不例外,物体所受的重力是因为受到了地球的吸引。
(2)重力的方向总是竖直向下的。
(3)水平桌面上的两个球靠在一起,只接触不产生形变,故两球之间无弹力作用。
(4)如果两物体间的接触面粗糙、存在相互作用的弹力且有相对运动(趋势),才存在摩擦力。
(5)动摩擦因数用比值 \(\frac{{{F_f}}}{{{F_N}}}\) 定义,跟两接触面的性质有关,而跟滑动摩擦力和压力均无关。
2.直梯受到重力 G、墙壁的支持力 FN1、地面的支持为 FN2 和静摩擦力 Ff,受力示意图如图所示。
3.把纸粘贴在木块的下表面,使纸跟水平桌面接触,用测力计水平拉木块做匀速运动,测出拉力 F 和木块的重力 G,由 Ff = F,FN = G,则 μ = \(\frac{{{F_f}}}{{{F_N}}}\) = \(\frac{F}{G}\)。多做几组实验,取 μ 的平均值。
4.以桶为研究对象,桶受到重力和两个拉力的作用处于静止状态,如图所示。设手的提力 F1 和 F2 与竖直方向的夹角均为 θ,根据共点力平衡条件有 F1 = F2 = \(\frac{{mg}}{{2\cos \theta }}\)。θ 越小,力 F1(或 F2)越小,可见两人手臂间的夹角小些省力。
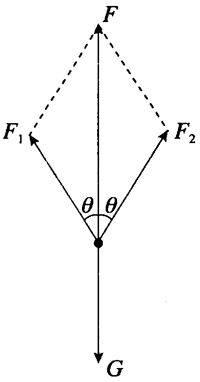
提示:两人共提一桶水,两人拉力的合力与桶的重力大小相等,根据合力一定,两个拉力夹角的变化可以判断其中一个拉力大小的变化。
5.以劈为研究对象,两侧向推力是力 F 的两个分力,它们大小相等,则 FN = \(\frac{F}{{2\sin \left( {\frac{\theta }{2}} \right)}}\)。
提示:在劈背施加力 F 后,产生垂直侧面的两个分力,使用中依靠这两个分力分开被劈的物体。
6.0.58 m
提示:以画框为研究对象,画框受到重力和两绳的拉力作用,设细绳的拉力为 F,它与竖直向上方向的夹角为 θ,则 2Fcosθ = G。
已知两挂钉的间距为 d = 0.5 m,设细绳长度为 l,则有几何关系 sinθ = \(\frac{d}{l}\)。联立解得 l = \(\frac{d}{{\sqrt {1 - {{\left( {\frac{G}{{2F}}} \right)}^2}} }}\)。
当 G、d 不变时,F 变大,l 变小。故当细绳的拉力最大时,绳长最短。代入数据解得 l = 0.58 m。
B 组
1.61 N;71 N
提示:如图所示,以小球为研究对象,小球受到重力 G、支持力 FN、拉力 FT 三个力的作用处于静止。根据正交分解,沿 x 轴方向有 FNsin37° = FTsin45°,沿 y 轴方向有FNcos37° + FTcos45° = G。解得 FN = \(\frac{5}{7}\)G,FT = \(\frac{{3\sqrt 2 }}{7}\)G。将 G = 100 N 代入得 FN = 71 N,FT = 61 N。
2.(1)133 N;167 N;(2)作用力都将变小
提示:(1)如图所示,设空调外机对 O 点的压力为 FN,则横梁对 O 点的拉力 FA = \(\frac{{{F_N}}}{{\tan 37^\circ }}\),斜梁对 O 点的压力 FB = \(\frac{{{F_N}}}{{\sin 37^\circ }}\)。解得 FA = \(\frac{4}{3}\)FN、FB = \(\frac{5}{3}\)FN。
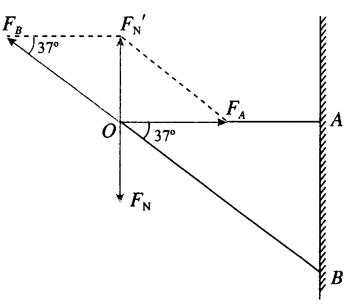
本题题干中,一台室调外机由两个三角形支架支撑,空调外机的重力为G = 200 N,则FN = \(\frac{G}{2}\) = 100 N。所以 FA = 133 N、FB = 167 N。
(2)如图所示,如果把斜梁加长一点,仍保持连接点 O 的位置不变,横梁仍然水平,由于 FN 不变,这时横梁对 O 点的作用力 FA′ 将变小,斜梁对 O 点的作用力 FB′ 也将变小。
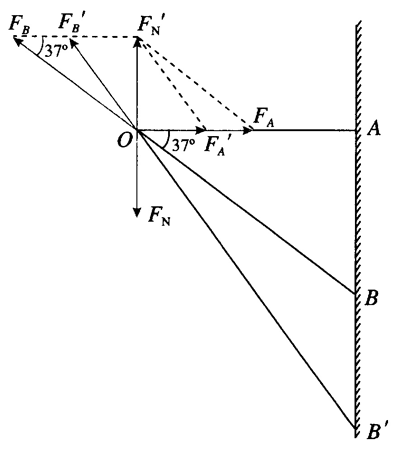
3.FA = 8 N;FB = 9 N
提示:若木块 A、B 滑动,则它们受到的滑动摩擦力 FfA = μFNA = μGA = 12.5 N,FfB = μFB = μGB = 15 N。压缩弹簧的弹力 FT = kx = 400×0.02 N = 8 N。
木块 B 在水平方向受到向右的拉力 F = 1 N、向右的弹力 FT = 8 N 和向左的摩擦力 FB 作用,由于 F + FT < FfB,所以木块 B 静止,受到的静摩擦力大小为 FB = F + FT = 9 N。
木块 A 在水平方向受到向左的弹力 FT = 8 N 和向右的摩擦力 FA 作用,由于 FT < FfA,所以木块 A 静止,受到的静摩擦力大小为 FA = FT =8 N。
4.G\(\frac{{2\sin \theta \cos \theta }}{{{{\cos }^2}\theta - {{\sin }^2}\theta }}\) 或 Gtan2θ
提示:木块沿斜面匀速下滑时,设沿斜面向上的摩擦力为 Ff,垂直于斜面向上的支持力为 FN,则 Ff = Gsinθ,FN = Gcosθ。解得木块与斜面间的动摩擦因数 μ = \(\frac{{{F_f}}}{{{F_N}}}\) = tanθ。
用水平力 F 将木块沿斜面匀速向上推时,沿平行于斜面向上建立 x 轴,沿垂直于斜面向上建立 y 轴,则 FN′ = Gcosθ + Fsinθ,Ff′ = Fcosθ − Gsinθ。又由 μ = \(\frac{{{F_f}^\prime }}{{{F_N}^\prime }}\),联立解得 F = G\(\frac{{2\sin \theta \cos \theta }}{{{{\cos }^2}\theta - {{\sin }^2}\theta }}\) = Gtan2θ。(由于学生的三角函数知识跟不上物理学习的进度,可以取答案为 F = G\(\frac{{2\sin \theta \cos \theta }}{{{{\cos }^2}\theta - {{\sin }^2}\theta }}\))
5.小球受到重力(大小、方向不变)、绳子拉力 FT(大小未知,方向不变)和力 F 的作用,处于三力平衡状态。G 与 FT 的合力应与力 F 大小相等,方向相反。将三力平移到同一个三角形中,由图可知,当绳子拉力 FT 的大小改变而方向不变时,力 F 的大小和方向均改变。力 F 与绳子的夹角为 α,则 α 的范围是 0≤ α < 180° − θ。
6.(1)\(\frac{{4\sqrt 3 }}{3}\)G;\(\frac{{2\sqrt 3 }}{3}\)G;
(2)\(\frac{{\sqrt {21} }}{3}\)G
提示:(1)以两个小球整体为研究对象,则Fa = \(\frac{{2G}}{{\cos 30^\circ }}\) = \(\frac{{4\sqrt 3 }}{3}\)G,Fc = 2Gtan30° = \(\frac{{2\sqrt 3 }}{3}\)G。
(2)以小球2为研究对象,则Fb = \(\sqrt {{G^2} + F_c^2} \) = \(\frac{{\sqrt {21} }}{3}\)G。
7.(1)拔河运动的规则是围绕着摩擦力来制定的。最大静摩擦力的大小跟压力大小有关,因此需要对人的体重进行限定;规则要求必须穿平底“拔河鞋”,鞋底不能有突出物,这是要保证运动员脚底在水平方向受的是摩擦力,而不能是突出物和地面凹坑之间的弹力。手对绳的拉力也是靠静摩擦力来实现的,最大静摩擦力的大小跟接触面压力、接触面材料有关,规则限定不准戴手套,是为了保证接触面材料这个因素的公平,使运动员仅凭手对绳的压力来把控最大静摩擦力。
(2)拔河时,可以认为静止的运动员受到重力 G、水平方向的绳子拉力 FT 和沿运动员身体方向的地面对脚的作用力 F 这三个共点力作用而处于平衡,F 的水平分力为静摩擦力 Ff,竖直分力为地面支持力 FN。当绳子上的拉力增大时,人要不被拉动,要求静摩擦力也增大。由共点力平衡可知,由于 FN = G 是不变的,F 与地面的夹角越小,Ff 就越大。因此,所以人要往后倾倒。
发布时间:2022/4/7 下午8:30:49 阅读次数:5808
