第七章 小结
解释交通法规中汽车刹车距离与车速之间的关系。
这是一个调查类活动,要求收集我国现行交通法规中关于最高车速和安全车距的规定和数据,结合汽车的刹车距离、驾驶员的反应时间等参数,运用动能定理分析说明这些规定的依据。活动以小组为单位合作完成,成果以小报形式进行展示与交流。
编制的小报中应包含以下内容:引用的数据及出处、必要的理论分析过程、机动车安全驾驶宣传。
为了保证交通安全,汽车在行驶过程中严禁超速,且车辆之间应该保持必要的安全距离。通过查阅相关资料、访问有关部门,收集关于汽车刹车距离与车速关系的数据,撰写调查报告。
活动要求:
(1)摘录相关资料中关于我国最高车速和安全车距的规定和数据,标明出处(如“……”摘自《×××》第××页)。
(2)将上述信息按照一定的逻辑顺序排列(可以用图表的形式)。
(3)运用动能定理对收集到的数据进行分析,阐述我国交通法规中有关条例的制定依据。
(4)以小报的形式进行展示与交流。
- 基本概念和基本规律
功:当物体在力的方向上发生位移时,称力对物体做了功。恒力对物体所做的功等于恒力大小、位移大小、恒力与位移之间夹角的余弦三者的乘积。
平均功率:一段时间内做的总功与做功时间的比。恒力与位移方向相同时,等于恒力大小与平均速度大小的乘积。
瞬时功率:当力与瞬时速度的方向相同时,等于力的大小与瞬时速度大小的乘积。
额定功率:机械在正常状态下长时间工作不应超过的功率最大值。
动能:物体的质量与速度的二次方乘积的一半。
动能定理:物体受到的合力所做的功等于物体动能的变化量。
重力势能:物理的重力与物体相对于零势能面高度的乘积。
弹性势能:发生弹性形变的物体由于各部分之间相对位置发生变化而具有的能量。
机械能:物体动能和势能的代数和。
机械能守恒定律:在只有重力和弹力做功的系统内,动能与势能相互转化,机械能总量不变。
- 基本方法
通过动能定理、机械能守恒定律的推导过程,体会理论演绎的方法。
通过验证机械能守恒定律的实验,学会分析和处理实验数据的方法。
通过应用机械能守恒定律解决问题的过程,体会守恒的思想,领悟从守恒的角度分析问题的方法。
- 知识结构图
- 判断下列关于功的说法是否正确,并简述理由?
(1)功有正负之分,所以功是矢量。
(2)力越大,力对物体所做的功就越多。
(3)力对物体不做功,物体的位移一定为零。
- 定性作出汽车以恒定速度沿斜坡向上行驶的过程中,汽车的动能、势能和机械能随汽车离地面高度变化的图像,并简述理由。
- 神舟飞船从发射升空至返回大致经历了以下四个阶段,判断各个阶段返回舱的机械能是否守恒,并简述理由。
(1)飞船发射升空。
(2)飞船在椭圆轨道上绕地球运行。
(3)飞船进行最后一圈绕地飞行时进入返回姿态,返回舱与推进舱分离,制动发动机点火,飞船持续下降预备进入大气层。
(4)飞船借助降落伞和反推发动机逐步减速穿越大气层,以 3 ~ 4 m/s的速度下降预备着陆。
- 起重机吊住质量为 m 的木箱,沿竖直方向以加速度 a 匀加速上升一段距离 h。重力加速度 g,不计空气阻力,求起重机对木箱所做的功。
- 小明身高 1.8 m,在运动会上参加跳高比赛时采取背越式跳法,起跳后恰能越过 1.8 m 高的横杆。估算小明为此做了多少功?(g 取 10 m/s2)
- 有研究表明,游泳时人受到水的阻力正比于人在水中速度的二次方。男子自由泳 100 m 和 800 m 的世界纪录分别为 46.91 s 和 452.12 s。试比较运动员创造以上两项世界纪录时所做的功和平均功率。
- 如图 7–48 所示,质量为 m 的物体在水平拉力 F 的作用下,由静止开始沿粗糙水平面向前运动 s1 后,撤去拉力 F,已知物体与水平面间的摩擦力为 Ff。求:
(1)刚撇去拉力时,物体的速度 v;
(2)物体滑行的最大距离 s2。
图 7–48
- * 研究机械能守恒定律的装置如图 7–49 所示,用光电门传感器测量摆锤释放后经过各个挡光片时的速度,结合各挡光片相对轨道最低点的高度和摆锤质量,可
以分析摆锤运动过程中机械能的变化。
某组同学在一次实验中,将挡光片等间隔放置在圆弧轨道上,部分实验数据如表 7–4 所示。
(1)在图 7–50 中用横轴表示高度 h,纵轴表示能量,绘制运动过程中摆锤重力势能 Ep、动能 Ek 及机械能 E 随高度 h 变化的图线。
(2)以下哪组数据最接近表格中 x、y 的合理取值?简述理由。
A.x = 0.089,y = 0.116 B.x = 0.098,y = 0.125
C.x = 0.103,y = 0.130 D.x = 0.106,y = 0.113
表 7–4
|
序号 |
1 |
2 |
3 |
4 |
5 |
|---|---|---|---|---|---|
|
高度 h / cm |
15.2 |
10.0 |
5.8 |
2.7 |
0.7 |
|
势能 Ep / J |
0.149 |
0.098 |
0.057 |
0.027 |
0.007 |
|
动能 Ek / J |
0.019 |
0.060 |
0.089 |
x |
0.106 |
|
机械能 E / J |
0.168 |
0.158 |
0.146 |
y |
0.112 |
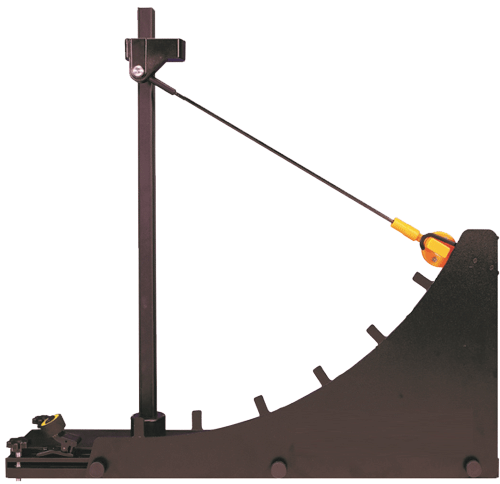
图 7–49
图 7–50
- * 某电动汽车动力性能参数如表 7–5 所示。汽车由静止开始匀加速启动,电机以额定功率工作后保持电机功率不变,继续加速 10 s 达到最大速度,假设行驶过程中汽车受到的阻力保持不变。求全过程中汽车的位移大小。
表 7–5
|
动力电池容量 / (kW·h) |
48.3 |
|---|---|
|
电机额定功率 / kW |
150 |
|
最高车速 / (km·h−1) |
135 |
|
整车质量 / kg |
1 710 |
|
0 ~ 50 km/h加速时间 / s |
4.2 |
- * 某汽车质量 m = 2 000 kg、发动机最大输出功率 Pm = 150 kW,以 v0 = 72 km/h 的速率匀速行驶时,发动机和传动与驱动系统内的功率分配关系如图 7–51 所示。已知水泵的功率 P1 恒定,传动与变速等内部机件摩擦而损耗的功率 P2 与汽车的行驶速率成正比,汽车行驶时所受的空气阻力 F阻1 与行驶速率 v 的关系为 F阻1 = kv2(k 为恒量),所受路面的阻力 F阻2 大小恒定。
(1)以 v0 匀速运动时,求汽车驱动力 F0 的大小。
(2)汽车以 v0 行驶时能产生的最大加速度大小为多少?
(3)汽车能否以 v = 3v0 的速率匀速行驶?简述理由。
图 7–51
- * 已知某公园中喷泉的喷水高度可达 h,任何时候都有体积为 V 的水处于空中,水的密度为 ρ。求该喷泉底部水泵的最小功率 P 和喷水管口的横截面积 S。
复习与巩固解读
1.参考解答:(1)不正确。虽然功有正负之分,但功是标量。
(2)不正确。根据 W = Fscosθ 可知,做功与位移和力都有关,力比较大但位移情况未知,物体所做的功无法确定。
(3)不正确。根据 W = Fscosθ 可知,当力与位移垂直或者力为零时,做功也为零,而此时物体的位移不一定为零。
命题意图:功的概念辨析。
主要素养与水平:科学推理(Ⅰ);能量观念(Ⅰ)。
2.参考解答:见图4。汽车以恒定速度沿斜坡向上行驶的过程中,汽车速度大小不变,高度随时间均匀增大,汽车的动能不变,势能和机械能随汽车离地面高度均匀增大。若选择出发位置为零势能面,则势能正比于高度。
命题意图:将真实情境转化为模型化情境,练习运用图像工具。
主要素养与水平:科学推理(Ⅰ);能量观念(Ⅰ)。
3.参考解答:(1)飞船发射升空过程中机械能不守恒。此过程发动机做功,飞船重力势能和动能都增加。
(2)机械能守恒。飞船在椭圆轨道上运行时,仅受地球万有引力作用,仅有地球万有引力做功,机械能守恒。
(3)机械能不守恒。制动发动机点火,对飞船做功,机械能不守恒。
(4)机械能不守恒。飞船借助降落伞和反推发动机逐步减速过程中,空气阻力和反推发动机对飞船做负功,机械能不守恒。
命题意图:在真实情境中判断机械能守恒定律适用条件。
主要素养与水平:模型建构(Ⅱ);科学论证(Ⅱ)。
4.参考解答:以木箱为研究对象,受到竖直向上的拉力 F 和重力 mg 作用以加速度 a 匀加速上升。根据牛顿第二定律知 F合 = F − mg = ma,故拉力 F = mg + ma。又已知位移竖直向上,大小为 h,可得拉力 F 对木箱所做的功 W = Fh = m(g + a)h。
命题意图:综合应用牛顿第二定律。
主要素养与水平:运动与相互作用(Ⅰ);科学推理(Ⅰ)。
5.参考解答:估计小明质量为 70 kg,起跳前的重心位于身高一半处约 0.9 m 高,起跳后重心达到的最大高度约为 1.8 m,忽略其水平速度可近似认为最大高度时速度为零。忽略阻力,起跳后只有重力做功,小明的机械能守恒,选地面为零势能面,有 Ek0 + mgh0 = Ekt + mght,代入数据,小明做功 W = Ek0 = mg(ht – h0) = 70×10×(1.8 − 0.9) J = 630 J。
命题意图:将真实情境转化为模型化情境。
主要素养与水平:模型建构(Ⅱ);科学椎理(Ⅰ)。
6.参考解答:忽略变速段和转向过程,将比赛全过程简化为匀速运动,动力等于水的阻力。
由条件知 100 m 和 800 m 比赛过程的平均速度为 2.132 m/s 和 1.769 m/s,故动力之比等于阻力之比,等于速度二次方之比为 1.453。
根据功的公式 W = Fs 可知,做功之比等于 0.182,所以 800 m 比赛过程做功多。
根据功率的公式 P = Fv 可知,做功功率之比等于速度三次方之比为 1.751,所以 100 m 比赛过程的平均功率大。
命题意图:在真实情境中建立简单模型,并解决定性半定量的问题。
主要素养与水平:模型建构(Ⅰ);科学推理(Ⅰ)。
7.参考解答:(1)以物体为研究对象,在拉力作用下向前运动 s1 过程中,拉力 F 和摩擦力 Ff 做功。根据动能定理,拉力 F 和摩擦力 Ff 做功的代数和等于动能变化量,即 Fs1 – Ffs1 = ΔEk = \(\frac{1}{2}\)mv2 − 0,故 v = \(\sqrt {\frac{{2(F - {F_f}){s_1}}}{m}} \)。
(2)对物体从静止开始运动到滑行停止的全过程分析可知,拉力 F 和摩擦力 Ff 做功,同样根据动能定理有 Fs1 – Ff(s1 + s2) = ΔEk = 0 − 0,故 s2 = \(\frac{{(F - {F_f}){s_1}}}{{{F_f}}}\)。
命题意图:运用动能定理解决简单问题。
主要素养与水平:模型建构(Ⅰ);科学推理(Ⅰ)。
8.参考解答:(1)见图5
(2)C。由已知数据可知,机械能逐渐减小,且经过相同路程机械能的减小量也逐渐增大,故选C(此题基于真实测量)
命题意图:实验误差分析。
主要素养与水平:科学推理(Ⅱ);能量观念(Ⅰ)。
9.参考解答:汽车在运动方向受到动力 F 和大小恒定的阻力 F阻 作用,以最大车速 vm = 135 km/h = 37.5 m/s 匀速运动时,由平衡条件知 F = F阻,又知道动力功率为电机额定功率 150 kW,有 P = Fvm = F阻vm,故
F阻 = \(\frac{P}{{{v_m}}}\) = \(\frac{{150000}}{{37.5}}\) N = 4 000 N
行驶过程中汽车受到的阻力保持不变,达到额定功率前动力保持恒定。可知汽车由静止开始经 4.2 s 匀加速达到 50 km/h ≈ 13.9 m/s,易知加速度 a ≈ 3.31 m/s2。由牛顿第二定律知 F合 = F – F阻 = ma,所以 F = ma + F阻 = (1 710×3.31 + 4 000)N = 9.66×103 N。
匀加速运动速度 v1 = at,动力功率 P = Fv = Fat,随时间均匀增加,达到额定功率时有 t1 = \(\frac{P}{{Fa}}\) = \(\frac{{150000}}{{9660 \times 3.31}}\) ≈ 4.69 s。
此过程位移 s1 = \(\frac{1}{2}\)at2 = \(\frac{1}{2}\)×3.31×4.692 m ≈ 36.4 m,动力做功 W1 = Fs1。达到额定功率后继续加速 t2 = 10 s,动力做功 W2 = Pt2 =150 000×10 J =1.5×106 J。
汽车由静止起动直至达到最大速度的全过程中,仅有动力 F 和大小恒定的阻力 F阻 做功,根据动能定理有
WF + W阻 = ΔEk
W1 + W2 – F阻s全 = \(\frac{1}{2}\)mvm2 − 0
联立并代入数值,解得 s全 ≈ 162 m。
全过程中汽车的位移大小约为162 m。
命题意图:在真实情境中建立模翌,从能量角度解决常见问题。
主要素养与水平:模型建构(Ⅰ);科学推理(Ⅲ)。
10.参考解答:(1)汽车在运动方向受到驱动力 F 和阻力 F阻 作用,其中阻力包含空气阻力 F阻1 和路面的阻力 F阻2,F阻 = F阻1 + F阻2。以 v0 = 20 m/s 匀速行驶时,汽车受力平衡,故 F0 = F阻 − F阻1 + F阻2。
由功率分配关系图知,此时驱动力功率 PF0 = P3 + P4 = (5 + 5)kW = 10 kW,又 PF0 = F0v0。
故 F0 = \(\frac{{{P_{F0}}}}{{{v_0}}}\) = 10×103÷20 N = 500 N
(2)由(1)中分析可知,汽车速率为 v0 时,阻力 F阻 = F0 = 500 N。
若发动机以最大输出功率 Pmax = 150 kW 工作,则驱动力功率 PF = Pmax − (P1 + P2) = [150 − (4 + 3)] kW = 143 kW,又F = \(\frac{{{P_{F0}}}}{{{v_0}}}\) =143×103÷20 N = 7150 N,由牛顿第二定律知 F合 = F − F阻 = ma,代入数值,解得 a ≈ 3.33 m/s2。
(3)不能。若汽车以速率 v = 3v0 匀速行驶,由题意知,水泵的功率 P1 恒定为 3 kW;传动损耗的功率 P2 与汽车的行驶速率成正比,为 12 kW;空气阻力 F阻1 = kv2,功率P阻1 = kv3 = 33×5 kW = 135 kW;路面的阻力 F阻2 大小恒定,功率 P阻2 = F咀2v =15 kW。
此时应有发动机输出功率 P = P1 + P2 + P阻1 + P阻2 = (3 + 12 + 135 + 15) kW = 165 kW,超出发动机最大输出功率 Pmax = 150 kW,故汽车不可能以速率 v = 3v0 匀速行驶。
命题意图:了解汽车的能量转化情况,从能量角度分析问题。
主要素养与水平:模型建构(Ⅱ);科学推理(Ⅲ)。
11.参考解答:忽略阻力作用,喷出的水在空中可视为做竖直上抛运动。v0 = \(\sqrt {2gH} \) 为水的初速度,即喷水管口处的水流速度,可得喷口单位时间喷出的水的体积,即流量 Q = v0S。又因为竖直上抛运动在空中的飞行时间 T = \(\frac{{2{v_0}}}{g}\),空中水的总体积为 V,有 V = QT = v0ST,故管口的横截面积 S = \(\frac{V}{{{ v_0}T}}\) = \(\frac{V}{{{v_0}T}}\) = \(\frac{{Vg}}{{2v_0^2}}\) = \(\frac{V}{{4H}}\)。
喷泉底部水泵的最小功率 P = \(\frac{1}{2}\)ρSv03 = \(\frac{1}{2}\)ρ\(\frac{V}{{4H}}\)(\(\sqrt {2gH} \))3 = \(\frac{{\rho gV}}{2}\sqrt {\frac{{gH}}{2}} \)。
(最小功率的详细推导参见教材第66页“拓展视野”)
命题意图:从能量角度分析流体问题。
主要素养与水平:模型建构(Ⅱ);科学推理(Ⅲ)。
发布时间:2022/2/12 上午11:10:33 阅读次数:4625
