第七章 第四节 重力势能

图 7–27 滑雪运动的连续影像
节首图通过连续影像展现滑雪运动过程中运动员离地高度的变化,可以让学生分析运动员上升和下落过程中重力做功以及重力势能变化的大致情况。
本节编写思路
本节以滑雪运动连续影像中运动员高度变化的情境引出,在“自主活动”小球下落撞击泡沫板的实验探究中引导学生经历猜想、设计、记录、分析、论证的过程,同时建立重力势能概念。
通过理论推演得到重力做功的特点和重力势能的定义,讨论重力做功与重力势能变化量的关系。
再结合“STSE”高空坠物的介绍和示例深化对重力势能的理解。
结合实例定性介绍弹性势能及其影响因素。本节借助“大家谈”讨论运动过程中重力势能、动能的变化情况。
学习中经历的实验探究过程有利于科学探究能力的培养和能量观念的形成。
举重运动员将杠铃举高的过程中,杠铃所具有的某种能量增加;水从高处流至水坝底部所释放的某种能量可以用来发电。我们在初中已经知道,这种由于物体高度改变而变化的能量叫做重力势能(gravitational potential energy),用 Ep 表示。图 7–27 所示的滑雪运动的连续影像中,运动员升高后再降低的过程就是运动员重力势能变化的过程。
图 7–28 小球对泡沫板的撞击
如图 7–28 所示,在水平桌面上铺一块厚薄均匀的泡沫板,让半径相同、质量不同的实心小球从不同的高度自由下落到泡沫板上,根据撞击产生凹痕的深浅猜想小球的重力势能与哪些因素有关。尝试用控制变量的思想设计实验方案并予以实施。
此处设置“自主活动”的目的是引导学生经历猜想、设计、记录、分析等过程,并运用证据论证猜想。活动中也可根据实际情况用松软的花泥、橡皮泥等代替泡沫板。
为了深入探讨重力势能的含义,我们先研究重力做功的特点。
图 7–29 重力做功
如图 7–29 所示,y 轴正方向竖直向上,水平地面处 y = 0。质量为 m 的物体沿任意路径 1 由 A 运动到 B ,位移为 s。位移与物体所受重力之间的夹角为 θ,A、B 离开水平地面的竖直高度分别为 hA、hB(即 A、B 的 y 坐标)。
由于此前已经分析过恒力做功的特点,故可以直接引用该结论得到重力做功的特点。
由于地表附近重力可视为恒力,根据恒力做功的计算式,这一过程中重力对物体所做的功
\[{W_{\rm{G}}} = mgs\cos \theta \tag{1}\label{1} \]
由图示几何关系可得
\[h = {h_A} - {h_B} = s\cos \theta \tag{2}\label{2}\]
式中,h 为 A、B 两点的竖直高度差。将式(2)代入式(1)得
\[{W_{\rm{G}}} = mgh = mg{h_A} - mg{h_B}\tag{3}\label{3}\]
由于图 7–29 中的路径 1 是任意选取的,这就表明,从 A 到 B 的过程中重力所做的功与路径无关,只取决于始、末位置之间的竖直高度差。
如果物体沿图 7–29 中的路径 2 从 B 返回 A,这一过程的位移与 s 等大反向,与重力的夹角为 π − θ。则物体返回过程中重力做功
\[{W_G}^\prime = mgs\cos (\pi - \theta ) = - mgs\cos \theta = - mgh\tag{4}\label{4}\]
这意味着,如果物体沿路径 1 和 2 组成的闭合路径运动一周,则
\[{W_{\rm{G}}} + {W_{\rm{G}}}^\prime = 0\]
即重力做功为零。
由上述推导过程可以得到重力做功的特点:
即重力做功仅取决于物体的始、末位置,而与物体经过的路径无关。或者说,沿任意闭合路径一周,重力做功为零。
与重力一样,弹簧的弹力、万有引力做功也与物体经过的路径无关,只取决于始、末位置,这样的力被称为保守力。在讨论了第一节问题与思考的第 2 题后,我们知道滑动摩擦力做功与物体经过的路径有关,或者说物体沿闭合路径运动一周摩擦力做功不为零,这种力被称为耗散力。空气、水等流体的阻力都是耗散力。
此处设置“拓展视野”是为了介绍弹力与万有引力做功的特点,说明保守力也可以是变力。此栏目内容供教师选用。
重力势能的定义是在重力做功性质的基础上提出的。物体的始、末位置一旦确定,重
力的功便确定下来。由式(3)可以发现,若令 Ep0 = mghA、EpB = mghB,则 Ep0 和 Ept 都是与物体位置有关的物理量。
将物体的重力 mg 与所在高度 h 的乘积称为重力势能,即
\[\color{#357A4A}{E_{\rm{p}} = mgh } \]
由于高度 h 具有相对性,所以重力势能也是相对的,只有在选取了重力势能为零的参考平面以后才能确定重力势能。
物理学中将重力势能为零的参考平面称为零势能面,h 就是物体相对于零势能面的高度。零势能面一般都是根据研究需要设定的。
若物体处于零势能面以上,则 h > 0,Ep > 0;处于零势能面以下,则 h < 0,Ep < 0。
实际情况下,物体总有一定的形状和大小。有时,物体的形态还会发生变化。计算实际物体的重力势能时,物体相对于重力势能零势能面的高度该如何确定?
此处设置“大家谈”的目的是引导学生讨论物体的形状对重力势能的影响。计算重力势能时,高度取物体重心到零势能面的距离。同一物体形态变化时,其重心位置会发生变化,故重力势能也会发生变化。
从根本上说,地球上的物体具有重力势能,是由于地球和物体间存在万有引力的相互作用,如果物体不受重力作用,就没有重力势能。所以重力势能是物体和地球这一体系所共有的。只是为简单起见,我们说物体具有重力势能。
图 7–30 地球对物体的引力
在地球附近的小尺度空间,地球对物体的引力可视作恒力,而在尺度与地球半径可以比拟的空间,地球对物体引力应被视作变力。若将地球看成质量均匀分布的球体,而将物体视作质点,地球对物体的引力总是指向地心,其大小仅与物体和地心间距离有关。如图 7–30 所示,物体沿任意曲线路径从 A 移到 B。在数学上可以证明,图中小段位移 s 上引力对物体做的功与沿地球径向 Ox 轴小段位移 sr 上引力所做的功相等。因此,物体沿 AB 移动过程中,引力所做的功等于沿地球径向 A′B′ 移动过程中,引力所做的功。由于从 A 到 B 的路径是任意的,所以引力做的功与路径无关,只取决于物体的始、末位置。万有引力和以后将要学习的库仑力具有类似的性质,这些力做功都与路径无关,是保守力。
由于地球和物体间万有引力而具有的势能称为引力势能,以无穷远处的引力势能为零,引力势能的表达式可写为 Ep = \( - \frac{{G{m_地}m}}{r}\) (式中 m地 为地球质量,m 为物体质量,r 为物体到地心的距离)。重力势能就是地球表面附近的引力势能。
此处设置“拓展视野”的目的是在更大的尺度上展示万有引力做功与路径无关,这也为以后学习库仑力做功的特点以及电势能打下基础。更详细的内容可参见节后资料链接“万有引力的保守性”。
由式(3)可知,重力做功引起物体重力势能的变化。用符号 ΔEp 表示某一过程中物体重力势能的变化量,并规定
重力做功与重力势能变化量之间的关系可通过教材第 74 页问题与思考第 2 题做具体说明。
\[\color{#357A4A}{\Delta {E_{\rm{p}}} = E_{{\rm{p}}t}^{} - {E_{{\rm{p0}}}}}\]
其中 Ep0 与 Ept 分别为物体在始、末位置的重力势能,则式(3)可以改写成
\[\color{#357A4A}{{W_{\rm{G}}} = - \Delta {E_{\rm{p}}}}\]
这就是重力做功与重力势能变化量之间的关系。具体而言就是:
物体下降,重力做正功,WG > 0,物体重力势能减少,ΔEp < 0;物体上升,重力做负功或物体克服重力做功,WG < 0,物体重力势能增大,ΔEp > 0。
必须注意,尽管重力势能取决于零势能面位置的选取,但重力势能的变化量与零势能面的选取无关。
重力势能是一种“潜在”的能量形式,在适当的条件下这种能量可以释放出来。有关高楼坠物的事故报道屡屡见诸报端,一次次事故引发全民关注高空坠物这一“悬在城市上空的痛”。据测算,从 4 楼落下的鸡蛋可把人头顶砸出肿包;从 8 楼落下会把头皮砸破;从 18 楼落下就会砸破头骨。如果从 25 楼落下……2019 年,国家规定故意从高空抛弃物品者将被依法追究刑事责任。防止高楼坠物,杜绝高空抛物,遵纪守法,请从我做起,从身边做起。
此处设置“STSE”旨在引导学生先估算鸡蛋在 4 楼、8 楼、18 楼所具有的重力势能,结合数据感受重力势能可能带来的危害,同时对学生进行安全意识和社会责任感教育。
示例 如图 7–31 所示,树上与 A 等高的 P 处有一个质量 m = 0.3 kg 的苹果下落。苹果有可能被人用篮子在与 B 等高处接住,也可能落到地面 C,还可能落到地面后滚入坑底 D 处。(g 取 10 m/s2)
示例通过零势能面的变换,让学生体验重力势能值与零势能面的选取有关,而重力势能的变化与零势能面的选取无关。
图 7–31 苹果的重力势能
(1)分别以 A、C、E 所在水平面为零势能面,求 P 处苹果的重力势能。
(2)苹果由 P 分别落至 C 或落至 D 的过程中,求重力所做的功以及重力势能的变化量。
分析:计算重力势能的关键是根据不同零势能面正确得出 P 的相对高度。而计算重力做功和重力势能变化量则与零势能面的位置无关。
解:(1)以 A 所在水平面为零势能面,P 的相对高度 hA = 0,则 P 处苹果的重力势能
\[{E_{\rm{p}}}_A = mg{h_A} = 0\]
以 C 所在水平面为零势能面,P 的相对高度 hC = 2.2 m,则 P 处苹果的重力势能
\[{E_{{\rm{p}}C}} = mg{h_C} = 0.3 \times 10 \times 2.2\;{\rm{J}} = 6.6\;{\rm{J}}\]
以 E 所在水平面为零势能面,P 的相对高度 hE = − 1.6 m,则 P 处苹果的重力势能
\[{E_{{\rm{p}}E}} = mg{h_E} = 0.3 \times 10 \times ( - 1.6)\;{\rm{J}} = - 4.8\;{\rm{J}}\]
(2)苹果由 P 落至 C 处,高度降低 ΔhC = 2.2 m,则
重力做正功 \({W_{\rm{G}}}_C = mg\Delta {h_C} = 0.3 \times 10 \times 2.2\;{\rm{J}} = 6.6\;{\rm{J}}\)
重力势能变化量 \(\Delta {E_{{\rm{p}}C}} = - {W_{\rm{G}}}_C = - 6.6\;{\rm{J}}\)
苹果由 P 落至 D 处,高度降低 ΔhD = 5.2 m,则
重力做正功 \({W_{\rm{G}}}_D = mg\Delta {h_D} = 0.3 \times 10 \times 5.2\;{\rm{J}} = 15.6\;{\rm{J}}\)
重力势能变化量 \(\Delta {E_{{\rm{p}}D}} = - {W_{\rm{G}}}_D = - 15.6\;{\rm{J}}\)
将图 7–32 所示的玩具青蛙拧紧发条后放在地上,玩具青蛙便能自行跳跃前进。图 7–33 所示的运动员张弓搭箭,蓄势待发,当他放开弓弦后,离弦之箭便飞驰而去。实际上,跳跃的玩具青蛙和飞驰而去的箭所获得的动能分别来自发条被拧紧和弓被拉开时发生弹性形变所蓄积的能量。
可以证明,在弹性限度内弹簧弹力所做的功只跟它初、末状态的形变量有关,与物体经过的路径无关,弹力是保守力;选取弹簧原长位置为零势能面,可得弹性势能满足 Ep = \(\frac{1}{2}\)kx2。

图 7–32 玩具青蛙

图 7–33 射箭运动
发生弹性形变的物体由于各部分之间相对位置发生变化而具有的能量叫做弹性势能(elastic potential energy)。对于具有弹性的物体而言,弹性形变程度越大,物体所具有的弹性势能也越大。以弹簧为例,弹簧不发生形变时的弹性势能为零。弹簧发生形变时,它所蓄积的弹性势能与弹簧的形变量和弹簧的劲度系数都有关系。在弹性限度内,若劲度系数一定,形变量越大,弹性势能越大;形变量一定,劲度系数越大,弹性势能越大。
物体发生弹性形变时会产生弹力的作用,弹力所做的功 W 与弹性势能变化量 ΔEp 之间的关系是
\[\color{#357A4A}{W = - \Delta {E_{\rm{p}}}}\]
这与重力做功和重力势能变化量的关系完全相同。
在撑竿跳和跳板跳水中,运动员起跳阶段分别借助了撑竿和跳板的弹性作用。请分析撑竿和跳板的弹性势能在运动员完成动作过程中的变化。
此处设置“大家谈”旨在引导学生定性分析运动过程中重力势能、动能和弹性势能的变化情况,可以尝试用柱状图表示其中若干标志性位置的弹性势能、重力势能与动能的定性关系。
- 判断下列关于重力做功和重力势能的说法是否正确,并简述理由?
(1)重力做多少正功,物体的重力势能就增加多少;重力做多少负功,物体的重力势能就减小多少。
(2)重力势能及其变化最都与零势能面的选取有关。
- 如图 7–34 所示,运动员从距地面高 h1 = 2.5 m 的 A 处投出一篮球,正中距地高 h3 = 3.05 m 的篮筐,球运动过程中到达的最高点 B 距地面高 h2 = 4 m。球的质量 m = 0.6 kg,g 取 10 m/s2。按要求在表 7–2 中填入数据?
图7–34
表 7–2
|
零势能面位置 |
篮筐 |
A 点 |
地面 |
|---|---|---|---|
|
篮球在 A 点的重力势能 |
|
|
|
|
篮球在 B 点的重力势能 |
|
|
|
|
从 A 到 B 过程中篮球重力做的功 |
|
|
|
|
从 A 到 B 过程中篮球重力势能的变化 |
|
|
|
图 7–35
- 图 7–35 所示为蹦床运动示意图。A 为运动员到达的最高点;B 为运动员下落过程中刚接触蹦床时的位置;C 为运动员到达的最低点。运动员自 A 落至 C 的过程中,运动员的重力势能和蹦床的弹性势能如何变化?
- 质量相等的均匀木球和铁球放在水平地面上,两球重力势能的大小关系与零势能面的选取是否有关?
- 跨越式跳高(图 7–36)已在专业的田径比赛中销声匿迹,专业运动员普遍采用背越式跳高(图 7–37)。试从重力势能的角度分析其原因。

图 7–36

图 7–37
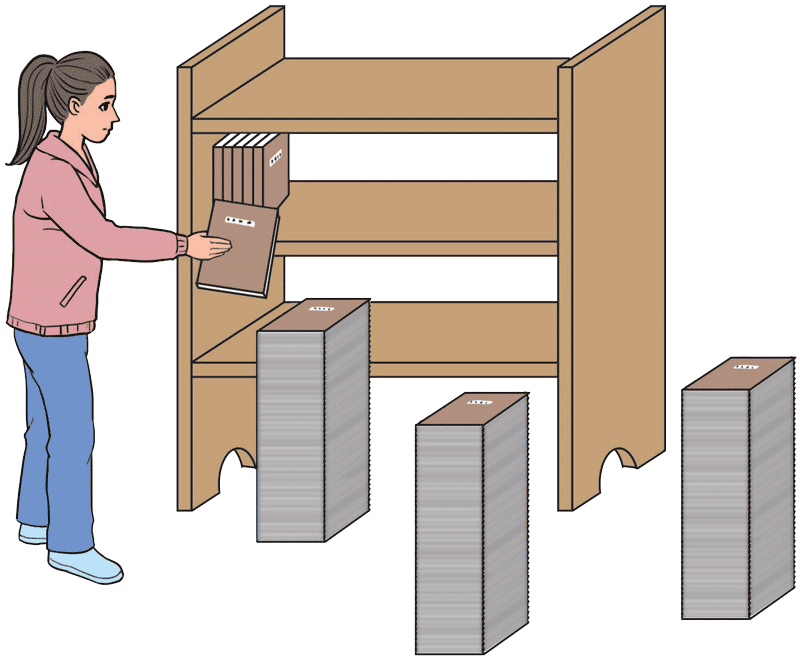
图 7–38
- 如图 7–38 所示,地上有 3 摞书,每摞 25 本。每本书尺寸均为 260 mm×185 mm×20 mm、质量均为 500 g。这些书刚好能放满一个三层书架,书架最低一层置物板距地面高 50 cm,相邻两层板的间距为 40 cm,g 取 10 m/s2。将书从地面放到书架的过程中,至少需做多少功?
问题与思考解读
1.参考解答:(1)不正确。根据 WG = − ΔEp 可知,物体下降时重力做多少正功,物体重力势能就减小多少;物体上升时重力做多少负功,物体重力势能就增大多少。
(2)不正确。根据 Ep = mgh,因高度 h 具有相对性,故而重力势能也是相对的,与零势能面的选取有关。又根据 WG = − ΔEp,WG 与零势能面的选取无关,可知重力势能变化量与零势能面的选取无关。
命题意图:深化做功与能量变化的关系,建立能量观念。
主要素养与水平:科学推理(Ⅰ);交流(Ⅰ)。
2.参考解答:− 3.3 J,5.7 J,− 9 J,增加 9 J,0,9 J,− 9 J,增加 9 J,15 J,24 J,− 9 J,增加 9 J。
命题意图:将真实情境转化为模型化情境,体验零势能面选取的作用。
主要素养与水平:能量(Ⅰ);科学推理(Ⅰ)。
3.参考解答:运动员自 A 落至 C 的过程中,重力对运动员做正功、重力势能不断减小;A 至 B 过程中,无弹力作用,弹性势能不变;B 至 C 过程中,弹力对运动员做负功,弹性势能不断增大。
命题意图:将真实情境转化为模型化情境,分析影响势能的因素。
主要素养与水平:模型建构(Ⅰ);科学推理(Ⅰ)。
4.参考解答:如图3所示,质量相等的均匀木球和铁球因为密度不同,放在水平地面上时木球重心位置更高。无论选取何处为零势能面,木球的重心高度更大,根据 Ep = mgh,且 mg 相等,故木球的重力势能也必然更大。若木球的质量大于铁球,则当选取高于木球重心高度某处为零势能面时,可能出现木球的重力势能小于铁的重力势能的情况。
命题意图:将真实情境转化为模型化情境,理解重心位置与重力势能的关系。
主要素养与水平:模型建构(Ⅰ);科学推理(Ⅱ)。
5.参考解答:观察教材图7–37可知,跨越式跳高时运动员的重心必须明显高于横杆,而背越式跳高时则较低。对同一位运动员而言,重心高度越高、重力势能越大,就要求运动员克服重力做功更多。由此可知,从克服重力做功角度来看背越式跳高具有明显优势。
命题意图:用能量观点解释真实问题。
主要素养与水平:模型建构(Ⅰ);科学论证(Ⅱ)。
6.参考解答:分析题意可知,初始时总质量 m = 37.5 kg 的3摞书整体重心高度在最大高度一半的位置 hc1 = 0.02×\(\frac{25}{2}\) m = 0.25 m,而摆满三层书架后整体重心在第二层书的中心高度处 hc2 = (0.5 + 0.4 + \(\frac{0.26}{2}\) )m = 1.03 m(考虑书长度 260 mm 的侧边竖立的姿态)。
根据 WG = − ΔEp 可知,至少需要克服重力做功 W = − WG = ΔEp = mghc2 – mghc1 = 37.5×10×(1.03 − 0.25)J = 292.5 J。
命题意图:将真实情境转化为模型化情境。此题常见的计算方法有:①隔离法:各层分别确定书籍中心位置、重力势能,再求和;②整体法:由质量分布确定三层书籍整体的重心,计算总重力势能。可比较两种做法,总结隔离法和整体法的特点。
主要素养与水平:模型建构(Ⅰ);科学推理(Ⅱ)。
参考资料
万有引力的保守性
就地球一物体这一体系而言,地球和物体间的引力是内力。设物体位移为 dr物 时,引力对物体做的元功为 dW物;而此时地球位移为 dr地,引力对地球做元功 dW地,则
dW物 = F物·dr物,dW地 = F地·dr地
式中,F物 和 F地 分别为地球与物体间相互作用的引力。引力做的总元功为
dW = dW物 + dW地
F物 和 F地 互为作用力和反作用力,F物 = − F地(物体运动速度远低于光速情况下)。因此
dW = F物·(dr物 – dr地)− F物·d(r物 – r地)= F物·dr地物= F物·dr
其中,r物 和 r地 分别为在我们所取的惯性参考系(例如这一体系的质心)中物体和地球的位置矢量。r物 – r地 = r地物 为由地心指向物体(视为质点)的位置矢量。令 r地物 = r,r 即为从地心指向物体的位置矢量,亦即地球参考系中物体的位置矢量。
由此可见,引力对体系做的总劝和地球参考系中引力对物体做的功相同。在地球参考系中,地球位移为零。将上式积分
\[\begin{array}{l}W = \int {dW = \int_A^B {{{\bf{F}}_地} \cdot d{\bf{r}}} } = \int_A^B {\frac{{G{m_地}m}}{{{r^2}}}( - {{\bf{r}}_0}) \cdot d{\bf{r}}} \\ = - G{m_地}m\int_A^B {\frac{{d{\bf{r}}}}{{{r^2}}}} = \frac{{G{m_地}m}}{{{r_{\rm{B}}}}} - \frac{{G{m_地}m}}{{{r_{\rm{A}}}}}\end{array}\]
式中,rA 和 rB 分别为地球参考系中物体的始、末点位置矢量的大小;r0 为由地球指向物体的单位矢量;负号代表引力,即引力指向地球;m 和 m地 分别为物体和地球的质量。
由上式可见,引力的功与物体和地球移动的路径无关,只取决于彼此初始和结束的相对位置,即由体系初始和结束的状态决定,而与状态间过渡的过程无关。综上所述,我们证明了引力是保守力。
以上讨论还表明,引力的保守性关键在于万有引力是各向同性的径向力,由此可知,凡相对某个中心各向同性的径向力必为保守力。点电荷的静电库仑力也具有同样的性质,也是保守力。而任意电荷分布产生的静电场的电场力为各个点电荷电场力的叠加,因此不仅匀强电场,任何静电场的电场力都必为保守力。分子间的相互作用虽然不满足二次方反比关系,但也是球对称的径向力,也是保守力。
发布时间:2022/2/11 下午8:42:48 阅读次数:8271
