第 1 章 功和机械能 第 4 节 势能及其改变

松软的白雪给人以恬静、美丽的印象。然而发生雪崩时（图 1-17），雪会以排山倒海之势摧毁沿途的一切，给自然界和人类带来灾难。雪崩破坏力强大是由于积雪处在一定高度而具有巨大的能量。这种能量有什么特点？它与积雪所处的高度有什么关系？与重力又有什么关系？本节将主要学习与重力势能及其改变有关的内容。

1．重力势能

物理学中，把物体因为处于一定的高度而具有的能量称为重力势能（gravitational potential energy）。例如，高处的石头、打桩时被举高的重锤、水电站储存的水等，都具有重力势能。

物体重力势能的大小与哪些因素有关？我们先通过一个小实验来回顾初中物理学习过的内容。

迷你实验室

影响小球重力势能大小的因素

准备两个大小相同、质量不同的光滑小球，在一盆中放入适量细沙。

在沙盆上方同一高度由静止释放两小球，小球落入细沙时会出现什么现象？是否质量大的小球陷得更深？让同一个小球分别从不同的高度由静止落下（图 1-18），又会出现什么现象？是否释放位置越高小球陷得越深？对比以上两种现象，你能得出什么结论？

由以上实验可知，重力势能的大小与物体的质量和所处的高度有关。物体的质量 m 越大，所处的高度 h 越高，重力势能就越大。在物理学中，物体的重力势能 E_p 表示为

E_p = mgh

重力势能是标量。它的单位与功的单位相同，在国际单位制中都是焦耳，符号为 J。

对同一物体，重力势能的大小由物体所处的高度决定。物体所处的高度总是相对一定的水平面而言，相对于不同的水平面，物体所处的高度是不同的。为了便于研究问题，我们一般先选定某一个水平面作参考。若把这个水平面的高度设为零，则物体在该水平面的重力势能也为零，这样的水平面称为零势能参考平面。例如，选定物体放在桌面上时重心所在的水平面 B 为零势能参考平面（图 1-19），当质量为 m 的物体重心位于该参考平面以上高度为 h₁ 的水平面 A 时，它的重力势能 E_pA = mgh₁ ；当物体放在桌面上时，它的重力势能 E_pB = 0 ；当物体放在地面上时，其重心在水平面 C 上，与水平面 B 的距离为 h₂，它的重力势能则为 E_pC = − mgh₂。

2．重力做功与重力势能改变的关系

我们知道，滑雪者靠重力可沿山坡滑下（图 1-20）。下面，我们通过对滑雪者滑雪模型的建构，进一步探索重力做功与重力势能改变的关系。

图 1-20 滑雪

首先，建构滑雪者及其滑雪过程的物理模型。如图1-21 所示，将滑雪者视为质量为 m 的物体（质点），物体从 A 点滑向 C 点，位移为 l，与竖直方向的夹角为 θ，A 点的高度为 h₁，C 点的高度为 h₂。根据功的定义，物体从A 点到 C 点过程中，重力做功为

W = mgl cosθ  = mg（h₁ − h₂） = mgh₁ − mgh₂

上式的结果正好等于物体从 A 点竖直下落到 B 点过程中重力所做的功。这表明，从 A 点到 B 点和从 A 点到 C 点，虽然路径不同，但重力做的功是相同的。其实，理论上可证明，无论物体沿哪条路径下滑（如图 1-21 中的曲线），其重力做功皆为 mgh₁ – mgh₂。由此可知，重力做功与始末位置的高度差有关，与路径无关。因此，滑雪者无论沿什么路线下滑，无论雪坡平缓还是陡峭，只要其始末位置的高度差相同，重力做功就相同。

物理聊吧

滑雪者下滑过程中会受到阻力的影响，甚至会受到滑雪杆或滑雪板的影响。在这种情况下，重力做功的多少会受到影响吗？

由重力做功的特点可知，重力做功与重力势能改变的关系为

W_G = E_p1 − E_p2 = − ΔE_p

式中，E_p1 = mgh₁ ，表示物体在初位置时的重力势能；E_p2 = mgh₂ ，表示物体在末位置时的重力势能。

物体从高处下落的过程中，W_G > 0，重力做正功，E_p1 > E_p2，重力势能减小；物体被举高的过程中，W _G < 0，重力做负功，即物体克服重力做功，E_p1 < E_p2，重力势能增大。总之，重力势能的改变是由重力做功决定的：重力对物体做多少正功，物体的重力势能就减小多少；物体克服重力做多少功，物体的重力势能就增大多少。物体的重力势能值与参考平面的选取有关，是相对的；而重力势能的改变量与参考平面的选取无关。

实际上，高处的物体在下落时对外做功。因此，重力势能可视为一种被暂时存储起来的潜在能量。在生产生活中，人们根据需要将重力势能转化成其他形式的能量。例如，建筑工地常用的打桩机就是把重力势能转化为动能，从而把桩钉打入地下；在江河中修筑堤坝提高水位，就可以利用水的重力势能发电（图 1-22）。

图 1-22 水力发电站利用水的重力势能发电

3．弹性势能及其改变

在射箭比赛中，运动员的手一松开，拉开的弓在恢复原状的过程中就能把箭发射出去（图 1-23）。可见，发生弹性形变的物体在恢复原状的过程中能够做功，说明它具有能量。物理学中，把物体因为发生弹性形变而具有的能量称为弹性势能（elastic potential energy）。拉开的弓弦、上紧的钟表发条等都具有弹性势能。在弹簧被拉长或被压缩时，弹簧中就存储了弹性势能；在恢复原状的过程中，弹簧就对外做功。理论研究表明，物体的弹性形变越大，具有的弹性势能就越大，恢复原状时对外做的功就越多。

用劲度系数不同的两根弹簧做实验，会发现弹性势能还与弹簧的劲度系数有关。在同样的形变下，劲度系数越大的弹簧弹性势能越大。因此，在生产生活中，人们会根据需要选用不同劲度系数的弹簧。

迷你实验室

小纸帽能弹多高

将圆珠笔里的弹簧取出，再用硬卡纸做个小纸帽，套在弹簧上（图 1-24）。用力把小纸帽往下压，使弹簧产生一定的弹性形变，然后迅速放开手，看看小纸帽能弹多高。

用大小不同的力使弹簧产生大小不同的弹性形变，重复做几次，看看小纸帽弹起的高度有什么不同。

换用不同劲度系数的弹簧做此实验，看看小纸帽弹起的高度又有什么不同。

在上面的实验中，弹簧在恢复原状的过程中对小纸帽做功。同时，随着弹簧迅速恢复到原状，弹性势能也减小到零，弹簧也就不再对外做功。研究表明，与重力做功的情况类似，弹簧的弹力对外做多少功，弹性势能就减小多少；反之，克服弹力做多少功，弹性势能就增大多少。

弹性势能和重力势能一样，都与物体间的相对位置有关：重力势能与物体和地球的相对位置有关，弹性势能与发生弹性形变的物体各部分的相对位置有关。人们把这类由相对位置决定的能量称为势能（potential energy）。势能是存储于一个物体系统内的能量，不是物体单独具有的，而是相互作用的物体所共有的。例如，重力势能是物体与地球所组成的“系统”共有的，没有地球，就谈不上重力，也谈不上重力势能。关于势能，我们在后面还将进一步学习。

节练习

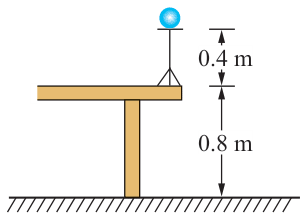
1．如图所示，水平桌面距地面 0.8 m，一质量为 2 kg 的小球放在距桌面 0.4 m 的支架上。小球可视为质点，取重力加速度 g ＝ 10 m/s²。

（1）以地面为零势能参考平面，计算小球具有的重力势能；若小球由支架落到桌面，重力势能减小多少？

（2）以桌面为零势能参考平面，计算小球具有的重力势能；若小球由支架落到桌面，重力势能减小多少？

（3）分析以上计算结果，你能得出什么结论？

【答案】（1）24 J，8 J

（2）8 J，8 J

（3）重力势能等大大小与零势能面的选取有关，重力势能的改变量与零势能面的选取无关。

2．一举重运动员将质量为 160 kg 的杠铃从地面举到了 1.8 m 的高度。取重力加速度 g ＝ 10 m/s² 。在此过程中，他对杠铃做了多少功？杠铃的重力势能改变了多少？

【答案】增加了 2 880 J。

3．质量为 m 的物体，在距地面高 h 处以 \(\frac{2}{3}\)g  的加速度由静止竖直下落到地面。在此过程中，物体的重力势能和动能的变化量分别是多少？

【答案】重力势能减小了 mgh，动能增加了 \(\frac{2}{3}\)mgh。

4．以初速度 v₀ 竖直向上抛出一质量为 m 的小球。假定小球所受的空气阻力 f 大小不变，已知重力加速度为 g，求：

（1）小球上升的最大高度；

（2）小球返回原抛出点时的速率。

【答案】（1）h = \(\frac{{mv_0^2}}{{2(mg + f)}}\)

（2）v = \(\sqrt {\frac{{mg - f}}{{mg + f}}} \)v₀

5．如图所示，质量为 M 的物体静止在地面上，物体上面连着一个轻弹簧。用手拉住弹簧上端将物体缓缓提升高度 H，则人做的功

A．等于 MgH             B．小于 MgH

C．大于 MgH             D．无法确定

【答案】C

*6．早期人们用不易弯曲的竹竿或金属杆进行撑竿跳高，后来采用了有弹性的玻璃纤维杆，如图所示，撑竿跳高的世界纪录也因此有了很大的提高。请上网查询，解释为何使用弹性玻璃纤维杆有助于撑竿跳高成绩的提高。

【答案】弹性玻璃纤维杆可承受的力大、弹性好，在运动员助跑结束时，这种杆能将运动员快速向前的动能很好地转化为杆的弹性势能，杆被压弯到最大弧度后，能将这部分弹性势能释放出来，并更多地转化为运动员的重力势能，帮助运动员越过横杆。

发布时间：2022/1/14 下午10:15:37  阅读次数：1557