第二章 第二节 自由落体运动的规律

图 2–7 游乐场里的“跳楼机”
跳楼机”是常见的游乐设施,其上半程运动与落体运动相似,可运用自由落体运动的规律分析其运动特点。
本节教材第 34 页的示例与此呼应。
本节编写思路
本节通过实验获得不同物体落体运动的 v–t 图像,得到速度与时间的关系,引出重力加速度。
通过分析 v–t 图像,获得自由落体运动位移与时间的关系。
利用实验结果通过演绎得到自由落体运动位移与速度的关系。
通过“示例”感受解决问题的过程与方法。
本节课所经历的探寻物理量之间关系的学习过程,有助于提升学生的科学思维能力。
结合推理与实验,伽利略发现自由落体运动是由静止开始的、速度随时间均匀增加的变速直线运动。可是,速度与时间的关系是通过观测下落的高度与时间的关系间接证实的;落体运动的结论是从斜面实验中“外推”出来的。我们能否通过实验直接研究自由落体运动并探索其运动规律呢?
图 2–8 研究篮球的自由下落
由前面学习可知,利用位移传感器可以研究自由落体运动的速度 v 随时间 t 变化的规律。
反射式位移传感器发射超声波脉冲,经被测物体反射后再被传感器接收。测量发射和接收超声波的时间差 Δt,根据超声波在空气中的波速 v,即可确定被测物体与传感器的距离为 v·\(\frac{{\Delta t}}{2}\),经计算机对数据处理后可进一步得到被测物体的位移、速度和加速度。
如图 2–8 所示,将反射式位移传感器固定在铁架台上。把篮球置于传感器正下方,由静止开始释放篮球,得到篮球的速度 v 与时间 t 的图像。
这里的“自主活动”是一个实验型活动,其目的是:
(1)利用位移传感器验证自由下落物体速度随时间变化的规律。
(2)测量自由下落物体的加速度。
在实验过程中,学生通过观察不同物体的下落,分析相应的 v–t 图像,归纳其共同特征。思考某些物体自由下落时的 v–t 图像与其他物体不同的原因,感受影响物体自由下落的因素。
除了用篮球做实验,还可以用黑板擦、书本、厚纸板等。用反射式位移传感器测量时,被测物体反射面的面积需不小于 4 cm2,释放位置与传感器的距离需大于 30 cm;同时周围应留出一定的空间,以防止反射波对实验的影响。除利用反射式位移传感器外,本实验也可用分体式位移传感器进行。
具体的实验指导可参见实验与活动部分的相关内容。
图 2–9 物体由静止开始下落
的 v–t 图像
在上述活动中,如果将物体从静止开始下落的时刻记为 0,那么物体下落的 v–t 图像为一条经过原点的直线,如图 2–9 所示。这说明速度 v 与下落时间 t 成正比,即 v = kt,k 为常量。这种速度随时间均匀增加的直线运动称为匀加速直线运动。
如果空气阻力可以忽略,物体自由下落的 v–t 图像均相同,斜率 k 为定值,由此引出重力加速度 g。
根据加速度的定义可得,该直线的斜率 k 就是这段运动的速度变化量 Δv 与所用时间 Δt 的比。该比值就是下落物体的加速度的大小。
在上述活动中,我们在同一地点,选择不同质量的“重物”做自由落体实验,发现它们均做匀加速直线运动,其加速度的数值在误差允许的范围内相等。
在物理学中,把自由落体运动的加速度称为重力加速度(gravitational acceleration),并用字母 g 来表示,方向竖直向下。
物体做自由落体运动时,其速度 v 与时间 t 的关系为
\[ \color{#035C87} {v = gt}\]
在地球上不同的地点测量发现,重力加速度 g 的大小会随纬度改变。表 2–2 中列出了地球上部分地点的重力加速度的大小。通常把重力加速度的大小取为 9.8 m/s2。
表中给出地球上不同地点重力加速度 g 的目的是使学生关注到,虽然在同一地点不同物体的重力加速度值相同,但是在不同纬度,同一物体重力加速度 g 的值略有不同。从而理解 g 通常取 9.8 m/s2 是忽略了地理位置的影响。
表 2–2 地球上部分地点的重力加速度的大小
|
地点 |
纬度 |
重力加速度 g/ (m·s−2) |
|---|---|---|
|
赤道海平面 |
0° |
9.780 |
|
广州 |
23°06ʹ |
9.788 |
|
武汉 |
30°33ʹ |
9.794 |
|
上海 |
31°12ʹ |
9.794 |
|
东京 |
35°43ʹ |
9.798 |
|
北京 |
39°56ʹ |
9.801 |
|
纽约 |
40°40ʹ |
9.803 |
|
莫斯科 |
55°45ʹ |
9.816 |
|
北极 |
90° |
9.832 |
重力加速度还受到当地地质等因素的影响。由于地质构造、矿产分布等地质原因会导致地球内部不同区域的密度不同,从而引起地表及其周围空间的重力加速度发生变化,这种变化称为重力异常。通过研究重力异常的变化和特征,可以得到地质构造、岩石分布和矿产贮量等信息。
对于速度随时间变化的直线运动,可以把整个运动时间分成 n 个小的时间间隔,且由于时间间隔 Δt 很小.在每一个 Δt 内物体的运动可近似看作匀速直线运动。我们用这种分时间间隔的匀速直线运动近似描述变速直线运动。从 v–t 图像上看,就是用“台阶”状的折线图像去无限逼近变速直线运动的图像,从而将匀速直线运动中 v–t 图像与时间轴包围的“面积”表示位移的结论推广到变速直线运动中。这是物理学中把“变”转化为“不变”进行研究的重要方法,称为无限分割与逼近的方法。这种方法在物理学的研究中有着广泛的应用。
“助一臂”栏目介绍了无限分割与逼近的方法。
图 2–10 做匀速直线运动物体
的 v–t 图像
做匀速直线运动物体的速度不随时间变化,其 v–t 图像是一条平行于时间轴的直线,如图 2–10 所示。匀速直线运动的特点是在任意相等的时间间隔 Δt 内,物体的位移相等,图中小矩形的面积表示物体在 Δt 时间内的位移,即 Δx1 = v1Δt = Δx2。
自由落体运动物体的 v–t 图像(图 2–9 )中,直线与时间轴之间所包围的面积是不是也可以表示物体 0 ~ t 时间内位移的大小呢?我们假设物体在下落过程中的每一小段时间间隔 Δt 内都做速度不同的匀速直线运动,如图 2–11(a)所示。每经过一个 Δt 的时间间隔,其速度大小就增加 Δv,图像为“台阶”状的折线。物体从零时刻起经过时间 t 后的位移大小等于折线下阴影部分各矩形面积之和。若 Δt 取得更小,Δv 也更小,如图 2–11(b)所示。此时折线下阴影部分的面积仍表示 0 ~ t 时间内物体的位移大小。当 Δt 趋近于零时,“台阶”状的折线就变成为一条过原点的直线,如图 2–11(c)所示。这就是自由落体运动的 v–t 图像,图中直线与时间轴所包围的“面积”就是自由落体运动经过时间 t 的位移大小。
在已知匀速直线运动 v–t 图像中直线下矩形面积的意义后,能否通过类比,猜想自由落体运动 v–t 图像中直线与时间轴包围的三角形面积也表示位移大小呢?
这是一个由特殊到一般的推理过程,不够缜密。
此处利用无限分割和逼近的思想证明该猜想是正确的。利用这一思想同样可以处理曲线下面积的问题。
图 2–11 v–t 图像与时间轴所包围的“面积”表示位移
这是一个数学推导的“自主活动”,目的是根据图 2–11 中的斜线通过数学演绎获得做自由落体运动物体的位移与时间关系式。
由图 2–11 可知
\[h = \frac{1}{2}{v_t}t\]
利用 vt = gt 即得
\[h = \frac{1}{2}g{t^2}\]
通过推导体验数学中的面积与物理图像中“面积”在形式上的相同与意义上的区别。
你能根据上述自由落体运动的 v–t 图像推导出做自由落体运动的物体从静止下落高度 h (即位移大小)与时间 t 的关系式吗?
图 2–12 小球自由下落的频闪照片
通过上述自主活动,可得物体做自由落体运动的下落高度 h (即位移大小)与下落时间 t 的定量关系为
\[ \color{#035C87} {h = \frac{1}{2}g{t^2}}\]
将上式与 v = gt 联立,消去时间 t ,推得自由落体运动的速度 v 与下落高度 h 之间的关系为
\[\color{#035C87}{{ v^2} = 2gh}\]
频闪摄影也可以用来研究自由落体运动。图 2–12 所示为小球做自由落体运动的频闪照片,照片拍摄时的频闪间隔为 \(\frac{1}{{20 }}\)s。分析照片可得自由落体运动下落高度 h 与时间 t 的关系。除此之外,还有多种方法可用于对下落物体定位、计时、测速。有兴趣的话,你也可以试一试。
由频闪照片可以获得在不同时刻的下落距离,利用数据可画出位移–时间图像。由图像特征,通过猜测,尝试画出位移–时间的二次方图像,证实猜测并得到规律。也可利用伽利略的方法,验证下落距离与所用时间的二次方之比为常量,进而得出规律。
可围绕定位、计时、测速等问题拓宽思路,提出更多的实验方案。譬如,用先电门测量速度,获得速度–时间图像;拍摄物体自由下落的视频,导入视频捕获与分析软件,获得位移–时间图像等。培养学生的发散思维能力。
示例 图 2–7 所示为游乐场中 62 m 高的游乐设施“跳楼机”。座椅带着游客升到最高点后竖直下坠。估算从最高点竖直下坠 15 m 需要多少时间。此时速度将达到多大?
“示例”呼应了节首图。目的是运用数学工具,解决实际问题。
“跳楼机”的运动可简化为两段:加速阶段和减速阶段。实际“跳楼机”加速阶段的运动受到空气阻力的影响,不是真正的自由落体运动。这里忽略空气阻力的影响,将“跳楼机”从最高点下坠 15 m 的运动视为自由落体运动。
示例中仅取下落的前 15 m 的原因是:
(1)根据最简单的模型,空气阻力正比于 ρSv2。粗略估算,“跳楼机”在下落的前 15 m 过程中所受空气阻力数量级为 103 N,所受重力数量级为 104 N。因此,用自由落体模型估算下落的前 15 m 的运动是可以接受的。
(2)《大型游乐设施安全规范》(GB 8408–2018)对跳楼机的最大下落速度有一定限制,因此下落过程中的大部分时间内应为减速运动。
分析:把游客和座椅视为质点,可将从最高点开始的下坠过程近似为自由落体运动。运用自由落体运动的规律可估算下坠时间 t 和下落速度 v 的大小。
解:以游客和座椅为对象,已知其从最高点下坠的高度 h = 15 m,根据自由落体运动位移与时间的关系 h = \(\frac{1}{{2}}\)gt2 可得所需时间
\[t = \sqrt {\frac{{2h}}{g}} = \sqrt {\frac{{2 \times 15\;{\rm{m}}}}{{9.8\;{\rm{m/}}{{\rm{s}}^2}}}} \approx 1.75\;{\rm{s}}\]
根据自由落体运动速度与时间的关系 v = gt ,可得下坠 15 m 时速度 v 的大小
\[v = gt = 9.8\;{\rm{m/}}{{\rm{s}}^{\rm{2}}} \times 1.75\;{\rm{s}} \approx 17.15\;{\rm{m/s}}\]
- 物体自由下落过程中,第 1 s 末、第 2 s 末、第 3 s 末的速度、加速度分别是多少?第 1 s 内、第 2 s 内、第 3 s 内速度分别增加了多少?
图 2–13
- 做自由落体运动的物体,在下落过程中单位时间内下落的高度随时间如何变化?写出判断的依据。
- 有同学通过实验得到自由落体运动的速度与时间满足 v = gt 的关系,将此关系代入 h = vt,从而得到自由落体运动的位移与时间的关系为 h = gt2。试对此做出评价。
- 如图 2–13 所示,两个小球分别从高度相同的 O 点和 Oʹ 点同时开始向下运动。图 2–13(a)中的小球以 10 m/s 的速度匀速运动,图 2–13(b)中的小球做自由落体运动。(g 取 10 m/s2)
(1)在图 2–13 中的两根直线坐标轴上分别画出两球在 0.5 s、1.0 s、1.5 s、2.0 s、2.5 s、3.0 s 时刻的位置。
(2)在同一个坐标平面内画出两球运动的 v–t 图像。
- 吐鲁番盆地的古代劳动人民为了适应干旱少雨的地理环境,巧妙地利用地形造了坎儿井(图 2–14)。从竖井口释放一颗小石子,测得从释放到听到小石子落到水面声音的时间为 2.5 s,试据此估测井内水面到井口的距离。
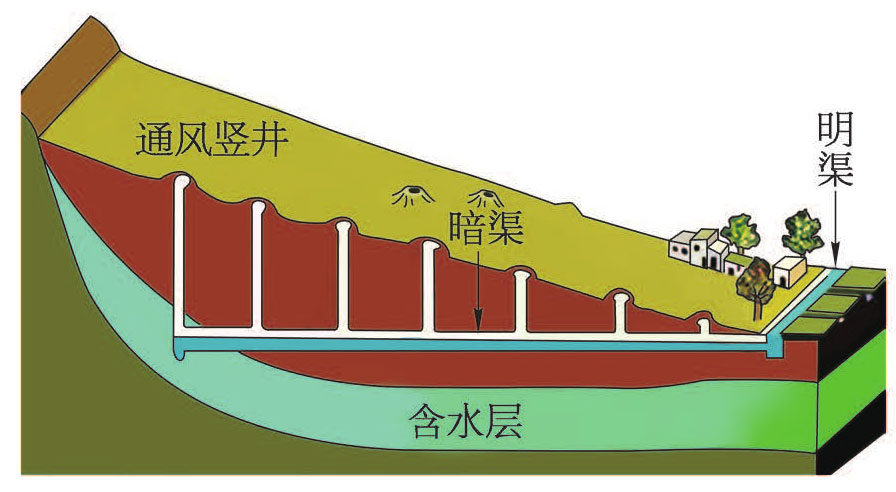
图 2–14
- 雨滴大约在 1.5 km 的高空生成并从静止开始下落。试根据自由落体运动的规律计算雨滴大约要经过多长时间才能到达地面?到达地面时的速度约为多少?你遇到过这么快的雨滴吗?另外,根据资料可知,落到地面的雨滴速度一般不超过 8 m/s,为什么与上述计算结果相差这么大?
问题与思考解读
1.参考解答:若重力加速度 g 取 10 m/s2,第 1 s 末、第 2 s 末、第 3 s 末的速度分别为 10 m/s、20 m/s、30 m/s,加速度均为 10 m/s2。第 1 s 内、第 2 s 内、第 3 s 内速度均增加了 10 m/s。
命题意图:简单运用自由落体运动的规律。
主要素养与水平:科学推理(Ⅱ)。
2.参考解答:物体在单位时间内下落的高度持续增加。判断依据:物体在单位时间内下落的高度 h = \(\frac{1}{2}\)gt2 – \(\frac{1}{2}\)g(t – Δt)2,其中 Δt = 1 s,化简后可知,下落高度随时间均匀增加。
命题意图:问题本身不复杂,需要学生将文字表述转化为关系式来进行判断。
主要素养与水平:科学推理(Ⅱ)。
3.参考解答:评价一:这位同学公式选错了,h = vt 的公式不适用于自由落体运动。评价二:自由落体运动物体的速度不是一成不变的,而是逐渐增加的。1 s 末的速度为 10 m/s,说明这 1 s 内的速度均小于 10 m/s,位移自然小于 10 m,h = gt2不正确
命题意图:通过评价,进行论证思路的梳理和概念的辨析。
主要素养与水平:科学论证(Ⅱ);质疑创新(Ⅰ);交流(Ⅰ)。
4.参考解答:如图所示。
命题意图:将匀速直线运动和自由落体运动进行对比,建立图像和位置变化的联系。
主要素养与水平:科学推理(Ⅱ)。
5.参考解答:以小石子为对象,下落时间为 2.5 s,小石子的速度不是很大,可忽略空气阻力的影响,将其运动视为自由落体运动。由于声音的传播速度远大于小石子下落的速度,可忽略声波传播的时间。估得距离约为 31 m。
命题意图:解题过程不是简单将数据代入公式,要说明忽略空气阻力和声音传播时间的原因。体会忽略次要因素、建构模型的方法。
主要素养与水平:模型建构(Ⅱ);科学推理(Ⅱ);社会责任(Ⅰ)。
6.参考解答:根据自由落体运动的规律,雨滴从 1.5 km 的高空自由下落到达地面的速度大小约为 173 m/s,所用时间约为 17.3 s。生活中没有这么快的雨滴。这是因为雨滴是从云层中滴落的,它的下落距离很长,雨滴在下落的过程中受到空气阻力的作用,且不能忽略不计,不能将其下落过程视为自由落体运动。
命题意图:自由落体运动是一种模型。认识模型建构需要考虑条件。
主要素养与水平:模型建构(Ⅱ);质疑创新(I);科学态度(I)。
资料链接
重力与万有引力
由于地球的自转,地面上静止的物体绕地球自转轴做圆周运动,所需的向心力 Fʹ 由物体所受地球万有引力 F 的一个分力提供,万有引力的另一个分力即为重力 mg,如图所示。因此
\[mg = \sqrt {{ F^2} + {{F'}^2} - 2FF'\cos \varphi } \]
式中 Fʹ = mω2r,由于 ω ≈ 7.292×10−5 rad/s,Fʹ ≪ F,近似后得
\[mg \approx F - F'\cos \varphi = m\left( {G\frac{{{m_地} }}{{r_地^2}} - {r_地}{\omega ^2}{{\cos }^2}\varphi } \right) = m{g_0}\left( {1 - \frac{{{r_地}{\omega ^2}}}{{{g_0}}}{{ \cos }^2}\varphi } \right)\]
式中 \({g_0} = G\frac{{{m_地} }}{{r_地^2}}\)。把地球的物理参数 m地、r地、ω 和引力常量 G 代入上式,可得地球表面附近物体的重力加速度 g ≈ g0(1 − 0.003 5cos2φ)。
发布时间:2021/7/8 下午5:29:46 阅读次数:15605
