用 Geogebra 绘制麦克斯韦速率分布曲线

2021年上海学业水平考试第5题考察了不同温度下分子速率的分布曲线，原题如下：

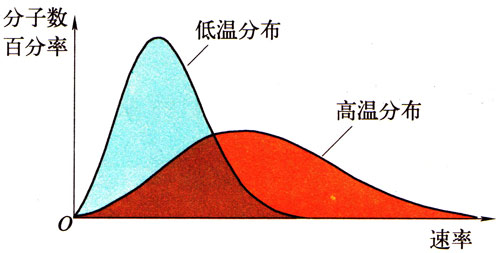
某理想气体在 T₁、T₂ 两个不同温度下的分子速率分布曲线如图所示。图中 f(v) 表示单位速率区间内的分子数占总分子数的百分比随分子速率 v 的变化关系，两曲线与横轴所围面积分别为 S₁、S₂，则【B】

A．T₁ ＞ T₂            B．T₁ ＜ T₂

C．S₁ ＞ S₂             D．S₁ ＜ S₂

2017年全国理综也有类似的题目：

氧气分子在 0 ℃ 和 100 ℃ 温度下单位速率间隔的分子数占总分子数的百分比随气体分子速率的变化分别如图中两条曲线所示。下列说法正确的是【ABC】

（A）图中两条曲线下面积相等

（B）图中虚线对应于氧气分子平均动能较小的情形

（C）图中实线对应于氧气分子在 100 ℃ 时的情形

（D）图中曲线给出了任意速率区间的氧气分子数目

（E）与 0 ℃ 时相比，100 ℃ 时氧气分子速率出现在 0 ~400 m/s 区间内的分子数占总分子数的百分比较大

两道题目中都考察了曲线所围面积的物理意义。麦克斯韦速率分布曲线的横轴表示速率，纵轴表示单位速率的分子数占总分子数的百分比，麦克斯韦速率分布曲线的面积的意义，就是将每个单位速率的分子数占总分子数的百分比进行累加，累加的结果是1。

翻翻教材，2007版上海科技出版社的教材内容如下：

以气体为例，气体的大量分子做无规则运动，但每个分子的速度大小（即速率）是不同的。对同一个分子而言，速率也时大时小，每个分子具有多大的速率完全是偶然的，但大量分子的速率分布却有一定的规律性。研究表明，这种大量分子速率分布的规律性是一种统计规律（图 6-11）。

分子速率分布的统计规律

气体的大多数分子，其速率都在某个数值附近，离开这个数值越远，分子数越少。

2019年版人民教育出版社的教材内容如下：

尽管分子做无规则运动，速率有大有小，但大量分子的速率却按一定的规律分布。下表是氧气分子在 0℃ 和100℃ 两种不同情况下的速率分布情况。图 1.3-2 是根据表格中的数据绘制的图像。

可以看到，0℃ 和 100℃ 氧气分子的速率都呈“中间多、两头少”的分布，但这两个温度下具有最大比例的速率区间是不同的：0℃ 时，速率在 300 ～ 400 m/s 的分子最多；100℃ 时，速率在 400 ～ 500 m/s 的分子最多。100℃ 的氧气，速率大的分子比例较多，其分子的平均速率比  0℃ 的大。从这里我们可以直观地体会“温度越高，分子的热运动越剧烈”这句话的含义。

从教材上可以看出，对于曲线面积的意义两本教材都没有涉及，学生能通过自己的分析能力得出结论要求较高。

闲来无事，想深入研究一下。找出大学课本抄个结论吧：在三维速度空间内，分子数占总分子数的比例为：

\[\frac{{dN}}{{{N_0}}} = 4\pi {\left( {\frac{m}{{2\pi kT}}} \right)^{\frac{3}{2}}}{v^2}\exp \left( { - \frac{{m{v^2}}}{{2kT}}} \right)dv\]

取

\[f(v) = 4\pi {\left( {\frac{m}{{2\pi kT}}} \right)^{\frac{3}{2}}}{v^2}\exp \left( { - \frac{{m{v^2}}}{{2kT}}} \right)\]

这就是麦克斯韦速率分布函数。f(v) 单位是速度单位的倒数 s/m（我原来一直以为单位是百分比呢！可能是因为上海教材的纵坐标表示为“分子数百分率”而不是“单位速率区间内的分子数占总分子数的百分比”，有点不太严密，从表达式上来说：“分子数百分率”为\(\frac{{dN}}{{{N_0}}}\)，而“单位速率间隔的分子数占总分子数的百分比”为 \(\frac{{dN}}{{{N_0}dv}}\)，而后者即 f(v)，因此面积的单位是一个无量纲的数字，上面已经说过，就是 1。

式中 m 为气体分子的质量，k 为玻尔兹曼常数取 1.38×10^-23 J/K，T 为温度。

由于分子质量 m 比较难记，我们还可以使用摩尔质量 M，有 M ＝ N_Am；而玻尔兹曼常量的定义为 k ＝ \(\frac{R}{{{N_A}}}\)，因此 \(\frac{m}{k}\)＝\(\frac{M}{R}\)，所以 f(v) 可以表达为：

\[f(v) = 4\pi {\left( {\frac{M}{{2\pi RT}}} \right)^{\frac{3}{2}}}{v^2}\exp \left( { - \frac{{M{v^2}}}{{2RT}}} \right)\]

式中 R 为气体常数，为 8.314 J/（mol·K），由于习惯上摩尔质量的单位取 g/mol，因此 R 代入 8 314。

此函数的最大值称为最概然速率。在相同的速率间隔之间，最概然速率附近的分子数最多。表达式为

\[{v_m} = \sqrt {\frac{{2kT}}{m}} = \sqrt {\frac{{2RT}}{M}} \]

知道了数学函数，利用 Geogebra 就可以很容易地画出曲线了。下面是主要步骤：

1．添加一个数值 R ＝ 8314；

2．添加两个数 T、M，并显示为滑动条。其中T的范围设置为 100 ～ 500，M 的范围设置为 2 ～ 50；

3．添加函数 f(x)＝如果(x ≥ 0, 4π sqrt((M / (2π R T))³) x² ℯ^((-M x²) / (2R T)))；

至此就可以绘制出曲线了。

4．添加数值 vm＝sqrt((2R T) / M)；

5．添加数值 p＝f(vm)；

6．添加点 A＝(vm,p)；

至此就可以显示最概然速率。例如，当温度为 300 K 时，氧气（摩尔质量为 32 g/mol）分子最概然速率为 394.83 m/s，这部分分子占分子总数的 0.21%。

7．添加数值 v1、v2，并显示为滑动条，范围设置为 0 ～ 1200。

8．添加数值“面积＝积分(f,v1,v2)”。

至此就可以显示 v1 ～ v2 速率区间分子数的百分比。例如，在 373 K 时，氧气分子的速率在 100 ～ 200 m/s 区间内的分子占总数的5.4%，与上面人教版教材给出的数据一致（人教版的图纵坐标为“速率区间百分比”，而不是“单位速率区间百分比”，因此纵坐标的值与下图有所不同）。若 v1 取 0，v2 取 1200（理论上应该取无穷大），发现面积约等于 1。

ggb源代码下载。

发布时间：2021/5/12 下午10:40:41  阅读次数：5420