第四章 第 1 节 电磁振荡

旅行者 1 号探测器是目前离地球最远的人造天体，它给我们发回了上万张神秘宇宙的照片。1990 年 2 月 14 日，已经完成主要任务的旅行者1 号在距离地球 60 亿千米之外接到了来自地球的指示，调转照相机，朝着地球的方向拍摄了一组照片。在传回地球的照片中，我们的地球是一个极小的暗淡蓝点，看不出与其他星球的区别。时至今日，我们仍然能够接收到 200 亿千米之外旅行者 1 号发来的信息。

电磁波的发现和使用带来了通信技术的发展，极大地改变了人们的生活，开阔了我们的视野。

他（麦克斯韦）从这组公式里算出了电磁波的速度，发现跟那时已知的光波的速度是一样的，所以他就肯定：光就是电磁波。这是1860年的一个重大贡献，这一发现把物理学中关于电、磁、光之间的关系整个地改观了。

——杨振宁

第四章 1 电磁振荡

问题？

水波是由机械振动形成的。一颗石子投入水面会激起一阵涟漪，但是要形成持续的水波，则需要不断地击打水面。电视、广播接收的是电磁波，要产生持续的电磁波，需要持续变化的电流。怎样才能产生这样的电流呢？

要产生持续变化的电流，可以通过线圈和电容器组成的电路实现。

演示

观察振荡电路中电压的波形

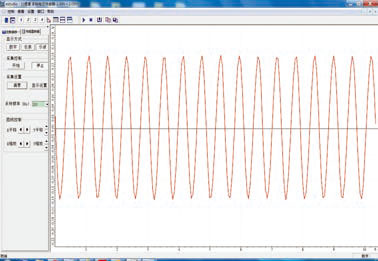
把线圈、电容器、电源和单刀双掷开关按照图 4.1-1 甲连成电路。把电压传感器（或示波器）的两端连在电容器的两个极板上。

先把开关置于电源一侧，为电容器充电；稍后再把开关置于线圈一侧，使电容器通过线圈放电。观察电脑显示器（或示波器）显示的电压的波形（图 4.1-1 乙）。

电磁振荡的产生

在前面的实验中，电路的电压发生周期性的变化，电路中的电流也发生周期性的变化。像这样大小和方向都做周期性迅速变化的电流，叫作振荡电流（oscillating current），产生振荡电流的电路叫作振荡电路（oscillating circuit）。

振荡电流实际上就是交变电流，不过习惯上指频率很高的交变电流。

图 4.1-1 甲中，当开关置于线圈一侧时，由电感线圈 L 和电容 C 组成的电路，就是最简单的振荡电路，称为 LC 振荡电路。

在开关掷向线圈一侧的瞬间，也就是电容器刚要放电的瞬间（图 4.1-2 甲 a），电路里没有电流，电容器两极板上的电荷最多。

电容器开始放电后，由于线圈的自感作用，放电电流不能立刻达到最大值，而是由 0 逐渐增大，同时电容器极板上的电荷逐渐减少。到放电完毕时（图 4.1-2 甲 b），放电电流达到最大值，电容器极板上没有电荷。

电容器放电完毕时，由于线圈的自感作用，电流并不会立即减小为 0，而要保持原来的方向继续流动，并逐渐减小。由于电流继续流动，电容器充电，电容器两极板带上与原来相反的电荷，并且电荷逐渐增多。充电完毕的瞬间，电流减小为 0，电容器极板上的电荷最多（图 4.1-2 甲 c）。

此后电容器再放电（图 4.1-2 甲 d）、再充电（图 4.1-2 甲 e）。这样不断地充电和放电，电路中就出现了大小、方向都在变化的电流，即出现了振荡电流。

在整个过程中，电路中的电流i（图 4.1-2 乙）、电容器极板上的电荷量 q（图 4.1-2 丙）、电容器里的电场强度 E、线圈里的磁感应强度 B，都在周期性地变化着。这种现象就是电磁振荡。

电磁振荡中的能量变化

思考与讨论

电磁振荡与机械振动虽然有着本质的不同，但它们还是具有一些共同的特点。在机械振动中，例如在单摆的振动中，位移 x、速度 v、加速度 a 这几个物理量周期性地变化。在电磁振荡中，电荷量 q、电流 i、电场强度 E、磁感应强度 B 这几个物理量也在周期性地变化。

在机械振动中，动能与势能周期性地相互转化。那么，在电磁振荡中，能量是如何转化的？

从能量的观点来看，电容器刚要放电时，电容器里的电场最强，电路里的能量全部储存在电容器的电场中；电容器开始放电后，电容器里的电场逐渐减弱，线圈的磁场逐渐增强，电场能逐渐转化为磁场能；在放电完毕的瞬间，电场能全部转化为磁场能；之后，线圈的磁场逐渐减弱，电容器里的电场逐渐增强，磁场能逐渐转化为电场能；到反方向充电完毕的瞬间，磁场能全部转化为电场能。所以，在电磁振荡的过程中，电场能和磁场能会发生周期性的转化。

如果没有能量损失，振荡可以永远持续下去，振荡电流的振幅保持不变。但是，任何电路都有电阻，电路中总会有一部分能量会转化为内能。另外，还会有一部分能量以电磁波的形式辐射出去。这样，振荡电路中的能量就会逐渐减少，振荡电流的振幅也就逐渐减小，直到最后停止振荡。

如果能够适时地把能量补充到振荡电路中，以补偿能量损耗，就可以得到振幅不变的等幅振荡（图 4.1-3）。实际电路中由电源通过电子器件为 LC 电路补充能量。

电磁振荡的周期和频率

电磁振荡完成一次周期性变化需要的时间叫作周期。周期的倒数叫作频率，数值等于单位时间内完成的周期性变化的次数。

思考与讨论

电容较大时，电容器充电、放电的时间会长些还是短些？线圈的自感系数较大时，电容器充电、放电的时间会长些还是短些？根据讨论结果，定性分析LC电路的周期（频率）与电容 C、电感 L 的关系。

理论分析表明，LC 电路的周期 T 与电感 L、电容 C 的关系是

\[T = 2\pi \sqrt {LC} \]

由于周期跟频率互为倒数，即 f ＝ \(\frac{1}{T}\)，所以

\[f = \frac{1}{{2\pi \sqrt {LC} }}\]

式中的周期 T、频率 f、电感 L、电容 C 的单位分别是秒 （s）、赫兹 （Hz）、亨利 （H）、法拉 （F）。

由以上两式可知，适当地选择电容器和电感线圈，就可以使振荡电路的周期和频率符合我们的需要。也可以用可调电容器或可调电感的线圈组成电路，改变电容器的电容或线圈的电感，振荡电路的周期和频率就会随着改变。

【例题】

在 LC 振荡电路中，线圈 L 的自感系数为 30 μH，可调电容器 C 的可调范围为 1.2 ~ 270 pF。求振荡电路的频率范围。

解 根据 LC 振荡电路的频率公式

\[{f_1} = \frac{1}{{2\pi \sqrt {LC} }} = \frac{1}{{2\pi \sqrt {30 \times {{10}^{ - 6}} \times 1.2 \times {{10}^{ - 12}}} }}{\rm{Hz}} = 2.65 \times {10^7}{\rm{Hz}}\]

\[{f_2} = \frac{1}{{2\pi \sqrt {LC} }} = \frac{1}{{2\pi \sqrt {30 \times {{10}^{ - 6}} \times 270 \times {{10}^{ - 12}}} }}{\rm{Hz}} = 1.77 \times {10^6}{\rm{Hz}}\]

此振荡电路的频率范围是 1.77×10⁶ ~ 2.65×10⁷ Hz。

如果没有能量损失，也不受其他外界条件影响，这时的周期和频率叫作振荡电路的固有周期和固有频率，简称振荡电路的周期和频率。

现代的实际电路中使用的振荡器多数是晶体振荡器（图 4.1-4），其工作原理与LC 振荡电路的原理基本相同。

练习与应用

1．一个 LC 电路产生电磁振荡。以横坐标轴表示时间，纵坐标轴既表示电流又表示电压，试在同一坐标系内，从某一次放电开始，画出该电路中电流和电容器两极板间电压随时间变化的 i-t 图像和 u-t 图像。

参考解答：如图所示

2．在上题图像中的一周期内，哪段时间电场能在增大？电场能最大时电流和电压的大小有什么特点？哪段时间磁场能在增大，磁场能最大时电流和电压的大小有什么特点？

参考解答：在 \(\frac{T}{4}\) ~ \(\frac{T}{2}\) 和 \(\frac{3T}{4}\) ~ T 时间内，电场能在增大；电场能最大时电流为 0，电压最大；在 0 ~ \(\frac{T}{4}\) 和 \(\frac{T}{2}\) ~ \(\frac{3T}{4}\) 时间内，磁场能在增大；磁场能最大时电流最大，电压为 0。

3．某收音机中的 LC 电路，由固定线圈和可调电容器组成，能够产生 535 kHz 到 1 605 kHz 的电磁振荡。可调电容器的最大电容和最小电容之比是多少？

参考解答：1∶9

4．为了测量储罐中不导电液体的高度，将与储罐外壳绝缘的两块平行金属板构成的电容 C 置于储罐中，电容 C 可通过开关 S 与电感L或电源相连，如图 4.1-5 所示。当开关从 a 拨到 b 时，由电感 L 与电容 C 构成的回路中产生振荡电流。现知道平行板电容器极板面积一定、两极板间距离一定的条件下，平行板电容器的电容与两极板间是否有电介质存在着确定的关系，当两极板间充入电介质时，电容增大。问：当储罐内的液面高度降低时，所测得的 LC 回路振荡电流的频率如何变化？

参考解答：增大

发布时间：2020/11/3 下午9:08:11  阅读次数：3483