气体压强的产生（图形动画）
气体的压强是大量分子的对器壁的碰撞产生的，求证：压强的公式为
\[p = \frac{1}{3}nm{\bar v^2}\]
其中，m是分子的质量，n是分子数密度，\({\bar v^2}\)是速度平方的平均值。进而求证：分子的平均平动动能为
\[{\bar \varepsilon _k} = \frac{3}{2}kT\]
不考虑分子之间的碰撞，演示分子运动的动画。
证明
一个分子对器壁的碰撞是断续的，它什么时候与器壁发生碰撞，在什么地方发生碰撞，给器壁施加了多大的冲量都是偶然的。但是大量分子时时刻刻与器壁碰撞，在宏观上就产生持续的压力，单位面积上的压力就是压强。
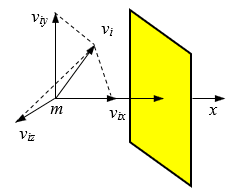如图1所示，取垂直于容器壁指向外侧的方向为x轴正向，设容器中理想气体分子的质量为m，某分子的速度为vi，三个分量分别为vix，viy，viz。由于碰撞是完全弹性的，所以碰撞前后y和z方向的速度分量保持不变，x方向的速度分量由vix变为-vix。根据动量定理，分子所受器壁的冲量为-mvix - （mvix） = -2mvix。根据牛顿第三定律，分子施加给器壁的冲量为
\[{I_i} = 2m{v_{ix}}\]
如图2所示，在容器壁上取一面积元dA，在一段时间间隔dt内，分子恰好与器壁发生碰撞时运动的距离为dli = vixdt。
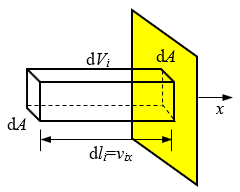
这个距离和面积元形成的柱体的体积为
\[d{V_i} = {\rm{ }}d{l_i}dA = {v_{ix}}dtdA\]
在所有以速度vi运动的分子中，只有位于柱体内的分子才能与器壁发生碰撞。单位体积内以速度vi运动的分子数为ni，所以柱体内这种分子数为
\[d{N_i} = {n_i}d{V_i} = {n_i}{v_{ix}}dtdA\]
这些分子施加给器壁的冲量为
\[d{I_i} = {\rm{ }}2m{v_{ix}}d{N_i} = 2m{n_i}{v_{ix}}^2dtdA\]
对所有速度求和即可求得所有分子施加给面积元的总冲量dI。但是速度条件限制为vix > 0，这是因为vix < 0的分子背离dA运动，在dt时间内不会与dA发生碰撞。可得
\[dI = \sum\limits_{_{i({v_{ix}} > 0)}} {d{I_i} = \sum\limits_{_{i({v_{ix}} > 0)}} {2m{n_i}v_{ix}^2dAdt} } {\rm{ }}\]
当气体处于平衡态时，气体分子朝x轴正向和负向运动的机会均等，平均来说，vix > 0和vix < 0的分子各占一半。
因此，将上式右边除以2就可以取消速度限制
\[dI = \sum\limits_i {m{n_i}v_{ix}^2dAdt} \]
这就是一群分子施加给器壁的冲量。根据冲量的定义可得气体施加给器壁的压力为dI/dt，所产生的压强为
\[p = \frac{{dI}}{{dtdA}} = m\sum\limits_i {{n_i}v_{ix}^2} \]
气体处于平衡态时，x方向速度平方的平均值为
\[\overline {v_x^2} = \frac{{\sum\limits_i {{n_i}v_{ix}^2} }}{n}\]
由于
\[\overline {v_x^2} + \overline {v_y^2} + \overline {v_z^2} = \overline {{v^2}} \]
所以
\[\overline {v_x^2} = \frac{{\overline {{v^2}} }}{3}\]
从而证得
\[p = nm\overline {v_x^2} = \frac{1}{3}nm\overline {{v^2}} \]
可见：气体分子的质量越大，速度平方的平均值越大，单位体积内分子的个数越多，气体产生的压强就越大。从公式的推导过程可知：压强是大量分子集体行为的宏观表现，是一个统计结果，单个分子不存在压强的概念。
根据阿伏伽德罗定律p=nkT，联立上式可得
\[\sqrt {\overline {{v^2}} } = \sqrt {\frac{{3kT}}{m}} \]
这是方均根速率。分子的平均平动动能为
\[\overline {{\varepsilon _k}} = \frac{1}{2}m\overline {{v^2}} = \frac{3}{2}kT\]
结果说明：大量分子的平均平动动能与绝对温度成正比，与气体种类无关。气体的温度是大量气体分子平均平动动能的量度，是大量分子无规则热运动的集体表现，具有统计的意义，单个分子或少数几个分子是没有温度概念的。这就是温度的微观实质。
图示
在一个平面上取1000个分子，初始状态如图3所示，箭杆表示分子运动的方向和相对大小，但是第一个分子例外，其箭杆特别长。当分子运动时，箭杆指示了第一个分子的运动方向。分子运动有快有慢，每时每刻都有分子与器壁发生碰撞，从而产生持续的压强。注意：由于不考虑分子的碰撞，而分子与器壁的碰撞是弹性的，因此一个分子的速率在运动中是不变的。实际上，分子之间存在着频繁的碰撞，正是通过分子间的碰撞，能量才能按自由度均分。
算法
按均匀分布随机产生分子的坐标，按正态分布随机产生分子的速度。不考虑分子之间的碰撞，分子在与器壁发生碰撞前做匀速直线运动。设分子速度为vx和vy，经过时间Δt，发生的位移分别为Δx=vxΔt和Δy=vyΔ。设分子的初始坐标为(x0,y0)，经过时间Δt的坐标分别为xt=x0+Δx和yt=y0+Δy。
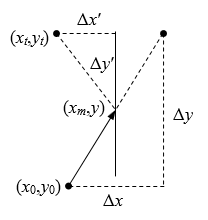如图4所示，当分子与右壁发生碰撞时，横坐标为xm，纵坐标为
\[y = {y_0} + \frac{{\Delta y}}{{\Delta x}}({x_m} - {x_0})\]
取(xm,y)为新的起点，碰撞后速度vx的方向发生改变，位移为
Δx′=-[Δx – (xm – x0)]，Δy′=-[Δy – (y – y0)]
从而可确定碰撞后的坐标：xi=xm+Δx′，yi=y+Δy′。
当分子与左壁（上壁或下壁）发生碰撞时，同样可求得碰撞点的坐标和碰撞后的坐标。
分子的个数是可调节的参数。
程序
%气体分子运动的动画(不考虑分子之间的碰撞)
clear %清除变量
n=input('请输入分子个数:'); %键盘输入分子个数
%n=1000; %不加箭杆时分子个数参考值
%n=50; %加箭杆时分子个数参考值
rand('state',0) %均匀分布随机数初始化
randn('state',0) %正态分布随机数初始化
xm=1.4e-6; %横坐标范围
ym=1e-6; %纵坐标范围
x0=xm*(2*rand(1,n)-1); %分子初始横坐标
y0=ym*(2*rand(1,n)-1); %分子初始纵坐标
figure %创建图形窗口
plot([-1,1,1,-1,-1]*xm,[-1,-1,1,1,-1]*ym,'LineWidth',3)%画器壁
axis equal off %使纵横坐标间隔相等
axis([-xm,xm,-ym,ym]) %设置坐标范围
title('气体分子与器壁的碰撞(不考虑分子间的碰撞)','FontSize',16)%标题
text(xm,ym,['\itN\rm=',num2str(n)],'FontSize',12)%显示粒子数
vx=randn(1,n); %分子x速度
vy=randn(1,n); %分子y速度
hold on %保持图像
for i=1:n %按分子循环
h(i)=plot(x0(i),y0(i),'.','MarkerSize',15,'Color',rand(1,3));%画点并取句柄
% hh(i)=quiver(x0(i),y0(i),vx(i),vy(i),1e-7);%画分子的箭杆取句柄
end %结束循环
hh=quiver(x0,y0,vx,vy); %画所有分子的箭杆取句柄
h1=quiver(x0(1),y0(1),vx(1),vy(1),1e-6);%画第一个分子的箭杆取句柄
dt=1e-7; %时间间隔
pause %暂停
set(hh,'UData',zeros(1,n),'VData',zeros(1,n))%去箭杆
%while 1 %无限循环
% if get(gcf,'CurrentCharacter')==char(27) break,end%按ESC键结束
while get(gcf,'CurrentCharacter')~=char(27)%不按ESC键循环
for i=1:n %按分子循环
xx=x0(i); %取横坐标
yy=y0(i); %取纵坐标
dx=vx(i)*dt; %取横位移
dy=vy(i)*dt; %取纵位移
if xx+dx>xm %如果超过右边界
y=yy+dy/dx*(xm-xx); %计算与右壁碰撞的纵坐标
set(h(i),'XData',xm,'YData',y)%设置点的坐标
x0(i)=xm; %右壁横坐标
y0(i)=y; %右壁纵坐标
dx=-(dx-(xm-xx)); %反弹横位移
dy=dy-(y-yy); %反弹纵位移
vx(i)=-vx(i); %速度反向
end %结束条件
if xx+dx<-xm %如果超过左边界
y=yy+dy/dx*(-xm-xx); %计算与左壁碰撞的纵坐标
set(h(i),'XData',-xm,'YData',y)%设置点的坐标
x0(i)=-xm; %左壁横坐标
y0(i)=y; %左壁纵坐标
dx=-(dx-(-xm-xx)); %反弹横位移
dy=dy-(y-yy); %反弹纵位移
vx(i)=-vx(i); %速度反向
end %结束条件
if yy+dy>ym %如果超过上边界
x=xx+dx/dy*(ym-yy); %计算与上壁碰撞的横坐标
set(h(i),'XData',x,'YData',ym)%设置点的坐标
x0(i)=x; %上壁横坐标
y0(i)=ym; %上壁纵坐标
dx=dx-(x-xx); %反弹横位移
dy=-(dy-(ym-yy)); %反弹纵位移
vy(i)=-vy(i); %速度反向
end %结束条件
if yy+dy<-ym %如果超过下边界
x=xx+dx/dy*(-ym-yy); %计算与下壁碰撞的横坐标
set(h(i),'XData',x,'YData',-ym)%设置点的坐标
x0(i)=x; %下壁横坐标
y0(i)=-ym; %下壁纵坐标
dx=dx-(x-xx); %反弹横位移
dy=-(dy-(-ym-yy)); %反弹纵位移
vy(i)=-vy(i); %速度反向
end %结束条件
x0(i)=x0(i)+dx; %新的起点横坐标
y0(i)=y0(i)+dy; %新的起点纵坐标
set(h(i),'XData',x0(i),'YData',y0(i))%设置点的坐标
% set(hh(i),'XData',x0(i),'YData',y0(i),'UData',vx(i),'VData',vy(i))%设置箭杆
end %结束循环
set(h1,'XData',x0(1),'YData',y0(1),'UData',vx(1),'VData',vy(1))%设置第一个分子的箭杆
drawnow %刷新屏幕
end %结束循环
quiver(x0,y0,vx,vy); %画所有分子的箭杆
说明
（1）程序执行时从键盘输入分子个数，例如1000。
（2）将正态分布随机数和均匀分布随机数初始化之后，可重复相同的运动，否则可演示不同的运动。
（3）分子的坐标是随机选取的。
（4）分子的速度也是随机选取的。
（5）用随机点表示分子，分子的颜色也是随机选取的。
（6）用箭杆表示分子速度的方向。
（7）第一个分子的箭杆单独画出来。如果要演示所有分子运动的方向，句柄要取在循环中，此句改为
hh(i)=quiver(x0(i),y0(i),vx(i),vy(i),le – 6);
（8）在显示分子初始状态后，按回车键就演示分子的运动。
（9）将分子箭杆的长度设置为零就消除了箭杆。
（10）设置分子的坐标就演示分子的运动。
（11）设置第一个分子的箭杆，可指示第一个分子的运动方向。如果要显示所有分子的速度方向，此句要放在循环中
set(hh(i),'Xdata’,x0(i),'YData', y0(i),'UData',vx(i),’VData',vy(i))
但是，如果分子数很多，分子运动就显得太慢。
（12）用简单的方法画第一个分子的轨迹，轨迹在分子与墙碰撞前有一点断裂。
（13）最后用箭杆表示分子运动的方向。
文件下载（已下载 23 次）发布时间：2019/5/21 下午12:17:07 阅读次数：4796
