第八章 2 气体的等容变化和等压变化

一定质量的某种气体，在体积不变时，压强随温度的变化叫做等容变化；在压强不变时，体积随温度的变化叫做等压变化。

气体的等容变化

法国科学家查理（J．A．C．Charles，1746～1823）在分析了实验事实后发现，当气体的体积一定时，各种气体的压强与温度之间都有线性关系（图8.2-1甲），我们把它叫做查理定律（Charles law）。

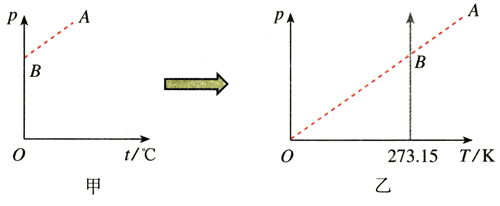
从图8.2-1甲可以看出，在等容过程中，压强p与摄氏温度t是一次函数关系，不是简单的正比例关系。但是，如果把图8.2-1甲中的直线AB延长至与横轴相交，把交点当做坐标原点，建立新的坐标系（图8.2-1乙），那么这时的压强与温度的关系就是正比例关系了。图乙坐标原点的意义为“气体压强为0时其温度为0”。可以证明，当气体的压强不太大、温度不太低时，坐标原点代表的温度就是热力学温度的零度。所以说，在p-T图象中，一定质量某种气体的等容线是一条通过坐标原点的直线。这时，查理定律可以表述为：一定质量的某种气体，在体积不变的情况下，压强p与热力学温度T成正比，即p∝T。写成等式的形式就是

p＝CT或\(\frac{p}{T}\)＝C

其中C是比例常数。

“压强p与热力学温度T成正比”也可以表示为另外的形式，即

\(\frac{{{p_1}}}{{{T_1}}}\)＝\(\frac{{{p_2}}}{{{T_2}}}\)或\(\frac{{{p_1}}}{{{p_2}}}\)＝\(\frac{{{T_1}}}{{{T_2}}}\)

气体的等压变化

也可以用实验研究一定质量的某种气体在压强不变的情况下其体积V与热力学温度T的关系。在V-T图象中，等压线是一条过原点的直线（图8.2-2）。

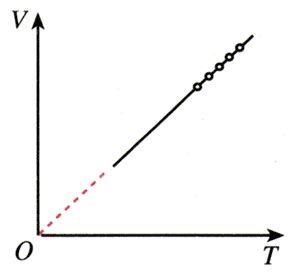
法国科学家盖-吕萨克（J．Gay-Lussac，1778～1850）首先通过实验发现了这一线性关系，我们把它叫做盖-吕萨克定律（Gay-Lussaclaw：一定质量的某种气体，在压强不变的情况下，其体积V与热力学温度T成正比，即

V＝CT或\(\frac{V}{T}\)＝C

其中C是比例常数。盖-吕萨克定律表示成另外的形式就是

\(\frac{{{V_1}}}{{{T_1}}}\)＝\(\frac{{{V_2}}}{{{T_2}}}\)或\(\frac{{{V_1}}}{{{V_2}}}\)＝\(\frac{{{T_1}}}{{{T_2}}}\)

【例题】如图8.2-3，某种气体在状态A时压强为2×10⁵ Pa，体积为1 m³，温度为200 K。

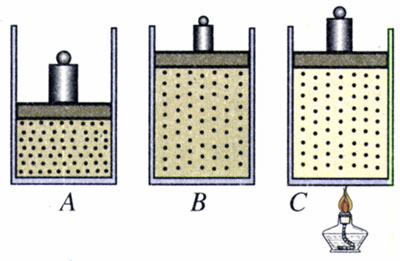
（1）它在等温过程中由状态A变为状态B，状态B的体积为2 m³。求状态B的压强。

（2）随后，又由状态B在等容过程中变为状态C，状态C的温度为300 K。求状态C的压强。

【解】（1）气体由状态A变为状态B的过程遵从玻意耳定律。

由

p_AV_A＝p_BV_B

得状态B的压强

p_B＝\(\frac{{{p_{\rm{A}}}{V_{\rm{A}}}}}{{{V_{\rm{B}}}}}\)＝\(\frac{{2 \times {{10}^5} \times 1}}{2}\)Pa＝10⁵ Pa

（2）气体由状态B变为状态C的过程遵从查理定律。

由

\(\frac{{{p_{\rm{B}}}}}{{{T_{\rm{B}}}}}\)＝\(\frac{{{p_{\rm{C}}}}}{{{T_{\rm{C}}}}}\)

得状态C的压强

p_C＝\(\frac{{{p_{\rm{B}}}{T_{\rm{C}}}}}{{{T_{\rm{B}}}}}\)＝\(\frac{{{{10}^5} \times 300}}{{200}}\)Pa＝1.5×10⁵ Pa

问题与练习

1．盛有氧气的钢瓶，在17℃的室内测得氧气的压强是9.31×10⁶ Pa。当钢瓶搬到－13℃的工地上时，瓶内氧气的压强变为8.15×10₆ Pa。钢瓶是不是漏气？为什么？

2．如图8.2-4，向一个空的铝制饮料罐（即易拉罐）中插入一根透明吸管，接口用蜡密封，在吸管内引入一小段油柱（长度可以忽略）。如果不计大气压的变化，这就是一个简易“气温计”。已知铝罐的容积是360 cm³，均匀吸管内部的横截面积为0.2 cm²，吸管的有效长度为20 cm，当温度为25℃时，油柱离管口10 cm。

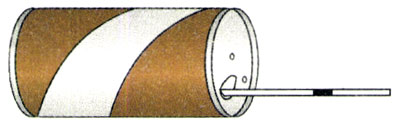
（1）吸管上标刻温度值时，刻度是否应该均匀？

（2）估算这个气温计的测量范围。

发布时间：2017/5/18 下午3:48:23  阅读次数：1641