第一章 3 电场强度
电场
万有引力曾被认为是一种既不需要媒介,也不需经历时间,而是超越空间与时间直接发生的作用力,并被称为超距作用。尽管牛顿本人不赞成这种说法,并指出:“没有其他东西做媒介,一个物体可以超越距离通过真空对另一个物体作用……在我看来,这种思想荒唐之极。”然而,他未能解决这个问题,因而仍然有人把万有引力说成是典型的超距作用。
库仑的平方反比定律似乎表明,静电力像万有引力一样,也是一种超距力。然而,超距作用的观点不可避免地带来一些神秘色彩,与人类的理智和科学追求不符,是18~19世纪的多数科学家难于接受的。使人们摆脱这一困境的是英国人法拉第,一位对事物本性有深刻洞察力的科学家。
19世纪30年代,法拉第提出一种观点,认为在电荷的周围存在着由它产生的电场(electric field),处在电场中的其他电荷受到的作用力就是这个电场给予的。例如,电荷A对电荷B的作用力,就是电荷A的电场对电荷B的作用;电荷B对电荷A的作用力,就是电荷B的电场对电荷A的作用(图1.3-1)。

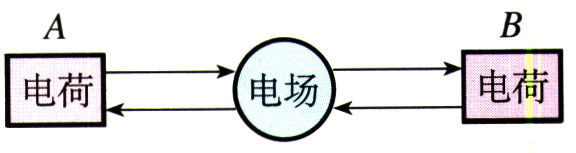
近代物理学的理论和实验证实并且发展了法拉第的观点。电场以及磁场已被证明是一种客观存在,并且是互相联系的,统称为电磁场(electromagnetic field)。变化的电磁场以有限的速度——光速,在空间传播。它和分子、原子组成的实物一样具有能量、质量和动量,因而场与实物是物质存在的两种不同形式。
应该指出的是,只有在研究运动的电荷,特别是运动状态迅速变化的电荷时,上述电磁场的实在性才突显出来。在本章中,只讨论静止电荷产生的电场,称为静电场(electrostatic field)。这种情况下,可以认为电场只是描述电荷相互作用的一种有效而且方便的方法。
电场强度
电场明显的特征之一是对场中其他电荷具有作用力,因此在研究电场的性质时,可以从静电力入手。
在上节图1.2-1的实验中,悬挂起来的带电小球受到带电金属球O的静电力,这表明带电金属球周围存在电场。从这个实验还可以看出,小球受到的静电力的大小和方向与小球的位置有关。这表明,电场的强弱是与位置有关的。
这里的分析就是一种猜想和假设,它的正确性有待实验的检验。
图1.2-1实验中的带电小球是用来检验电场是否存在及其强弱分布情况的,称为试探电荷,或检验电荷;被检验的电场是带电金属球O所激发的,所以金属球O所带的电荷称为场源电荷,或源电荷。试探电荷的电荷量和尺寸必须充分小,对金属球O上的电荷分布不产生明显的影响,从而原来的电场不因试探电荷的出现而有明显的变化。
我们不能直接用试探电荷所受的静电力来表示电场的强弱,因为对于电荷量不同的试探电荷,即使在电场的同一点,所受的静电力也不相同。然而,人们会很自然地想到,如果把一个很小的电荷q1用做试探电荷,它在电场中的某个位置受到的静电力是F1,另一个同样的电荷在同一位置受到的静电力一定也是F1;现在把两个这样的电荷一同放在这里,它们总的电荷量是2q1,它们所受的合力很可能就是2F1。依此类推:三个这样的电荷放在这里,电荷量是3q1,受到的静电力可能是3F1……也就是说,试探电荷在电场中某点受到的力F很可能与试探电荷的电荷量q成正比
F=Eq (1)
式中E是比例常数,与试探电荷q无关。
实验表明,我们的推测是正确的:试探电荷在电场中某个位置所受的力,的确与试探电荷的电荷量成正比。实验还表明,在电场的不同位置,(1)式中的比例常数E一般说来是不一样的,它反映了电场在这点的性质,叫做电场强度(electric field strength)。根据(1)式我们知道
E=\(\frac{F}{q}\) (2)
在物理学中,常常用比值定义物理量,用来表示研究对象的某种性质。例如,用质量m与体积V的比值定义密度、用位移l与时间t的比值定义速度v、用静电力F与电荷量q的比值定义电场强度E,等等。这样定义一个新的物理量的同时,也就确定了这个新的物理量与原有物理量之间的关系。
在日常生活中也常遇到类似的情况,购买物品时的“单价”就是一例。此外,“人均国民生产总值”“人均占有耕地面积”等,实际上都是用比值定义的。
在今后的学习中,还会遇到用比值定义的物理量。
按照(2)式,电场强度的单位应是牛[顿]每库[仑],符号为N/C。如果1 C的电荷在电场中的某点受到的静电力是1 N,这点的电场强度就是1 N/C。电场强度的另一个单位是伏[特]每米,符号是V/m,它与牛每库相等,即1 V/m=1 N/C[1]。
电场强度是矢量。物理学中规定,电场中某点的电场强度的方向跟正电荷在该点所受的静电力的方向相同。按照这个规定,负电荷在电场中某点所受的静电力的方向跟该点的电场强度的方向相反。
点电荷的电场 电场强度的叠加
电场强度是描述电场性质的物理量,在静电场中,它不随时间改变。图1.2-1的实验表明,在某一电荷产生的电场中,不同位置的电场强度一般是不同的。电场强度与产生它的场源电荷有什么关系呢?
点电荷是最简单的场源电荷。设一个点电荷的电荷量为Q,与之相距r的试探电荷的电荷量为q,根据库仑定律,试探电荷所受的力为
F=k\(\frac{{Qq}}{{{r^2}}}\)
依电场强度的定义,E=\(\frac{F}{q}\),所以,该点电场强度的大小为
E=k\(\frac{Q}{{{r^2}}}\)
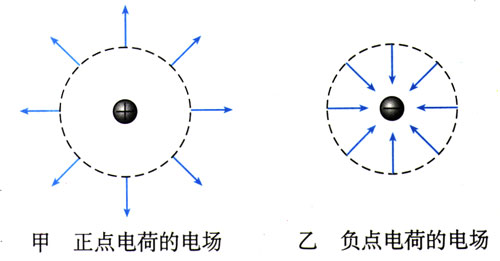
如果以Q为中心作一个球面(如图1.3-2),则球面上各点的电场强度大小相等。当Q为正电荷时,E的方向沿半径向外;当Q为负电荷时,E的方向沿半径向内。
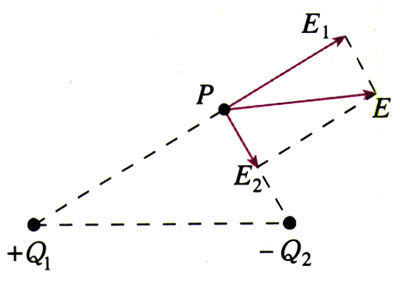
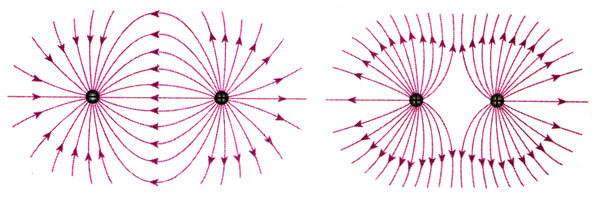
如果场源是多个点电荷,事实表明,电场中某点的电场强度为各个点电荷单独在该点产生的电场强度的矢量和。这说明电场的作用是可以相互叠加的。例如,图1.3-3中P点的电场强度,等于+Q1[2]在该点产生的电场强度E1与-Q2在该点产生电场强度E2的矢量和。
一个比较大的带电物体不能看做点电荷。在计算它的电场时,可以把它分做若干小块,只要每个小块足够小,就可以把每小块所带的电荷看成点电荷,然后用点电荷电场强度叠加的方法计算整个带电体的电场。
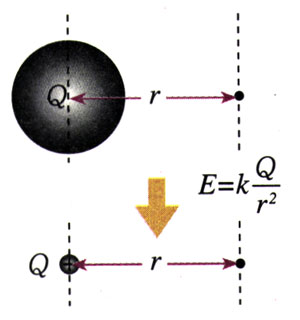
可以证明,一个半径为R的均匀带电球体(或球壳)在球的外部产生的电场,与一个位于球心的、电荷量相等的点电荷产生的电场相同,球外各点的电场强度也是
E=k\(\frac{Q}{{{r^2}}}\)
式中的r是球心到该点的距离(r>R),Q为整个球体所带的电荷量。
电场线
形象地了解和描述电场中各点电场强度的大小和方向也很重要。法拉第采用了一个简洁的方法描述电场,那就是画电场线(electric field line)。
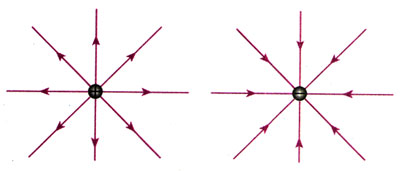
电场线是画在电场中的一条条有方向的曲线,曲线上每点的切线方向表示该点的电场强度方向(图1.3-5)。从图1.3-6和图1.3-7可以看出,电场线有以下几个特点:
(1)电场线从正电荷或无限远出发,终止于无限远或负电荷;
(2)电场线在电场中不相交,这是因为在电场中任意一点的电场强度不可能有两个方向;
(3)在同一幅图中,电场强度较大的地方电场线较密,电场强度较小的地方电场线较疏,因此可以用电场线的疏密来表示电场强度的相对大小。
演示
模拟电场线
电场线的形状可以用实验来模拟。把头发屑悬浮在蓖麻油里,加上电场,微屑就按照电场强度的方向排列起来,显示出电场线的分布情况。图1.3-8是两种情况下的照片。

应该指出,电场线不是实际存在的线,而是为了形象地描述电场而假想的线。这个实验只是用来模拟电场线的分布。
在图1.3-9中,带电人体的头发由于静电斥力而竖起散开,其形状也大致显示出电场线的分布。

科学漫步
法拉第和场的概念
相隔一定距离的电荷或磁体间的相互作用是怎样发生的?这是一个曾经使人感到困惑、引起猜想,而且有过长期争论的科学问题。19世纪以前,不少物理学家主张超距作用的观点。
在引力作用是怎样发生的问题上,牛顿虽不赞成超距作用,但没有提出自己的观点,并声称“不做假说”。与牛顿不同,法拉第在电磁作用问题上明确了自己的见解。他在实验中发现,电作用和磁作用跟电荷之间或磁体之间的介质有关。在不同的介质中进行同样的实验,作用效果不同。这引起法拉第对电磁作用本质的深思。他认为,电力和磁力不可能是超越空间并与介质无关的超距作用,并提出:电荷或磁体在空间产生电场或磁场,正是通过场,才把电作用或磁作用到别的电荷或磁体。
法拉第不仅提出了场的概念,而且直观地描绘了场的清晰图像。他用电力线(即电场线)和磁力线(即磁感线)形象地描述电场和磁场。力线密的地方场就强,力线疏的地方场就弱;力线上每一点的切线方向表示场强的方向。法拉第用这幅图像说明了诸多电磁现象。例如,1831年他发现电磁感应现象后,借助于磁力线很快地对这一现象做出了清晰的表述:只要通过闭合电路的磁力线数目发生变化,电路里就会产生电流。
对于电磁理论而言,法拉第的场的概念还处于萌芽状态。他不精通数学,他提出的仅是一种不涉及精确的数学工具的描述方法。二三十年之后,麦克斯韦把法拉第关于电磁场的朴素而简单的图像,转换成精致而定量的描述,进而预言了电磁波的存在,并且把光现象与电磁现象统一起来。于是场的概念取得了成功,并日益得到发展。
应该指出的是,法拉第当年确信空间处处存在着有形的力线,如今人们已经不再认同这一看法。既然如此,为什么人们对法拉第的图像还念念不忘呢?
在电磁学发展的初期,法拉第的力线观念给予人们一种物理思想,犹如一座大厦建成以前的“脚手架”,在大厦建成之后,脚手架被拆除了,但这并不意味着脚手架就不重要了。或许今天我们的一些认识正是未来科学大厦的脚手架呢!
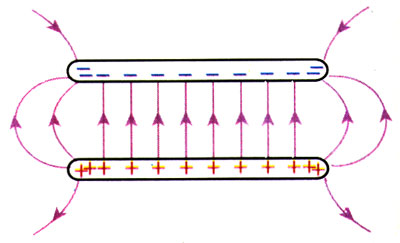
匀强电场
如果电场中各点电场强度的大小相等、方向相同,这个电场就叫做匀强电场(uniform electric field)。由于方向相同,匀强电场中的电场线应该是平行的;又由于电场强度大小相等,电场线的密度应该是均匀的。所以匀强电场的电场线是间隔相等的平行线。
带有等量异号电荷的一对平行金属板,如果两板相距很近,它们之间的电场,除边缘部分外,可以看做匀强电场。在两板的外面几乎没有电场。
问题与练习
1.把试探电荷q放到电场中的A点,测得它所受的静电力为F;再把它放到B点,测得它所受的静电力为nF。A点和B点的场强之比EA/EB是多少?再把另一电荷量为nq的试探电荷放到另一点C,测得它所受的静电力也是F。A点和C点的场强之比EA/EC是多少?
2.氢原子中,电子和质子的平均距离是5.3×10-11 m。质子在离它这个距离的位置产生的电场强度是多大?方向如何?电子受到的静电力是多大?方向如何?
3.场是物理学中的重要概念,除了电场和磁场,还有引力场。物体之间的万有引力就是通过引力场发生作用的,地球附近的引力场叫做重力场。仿照电场强度的定义,你认为应该怎样定义重力场强度的大小和方向?
4.有的同学说,电场线一定是带电粒子在电场中运动的轨迹。这种说法对吗?试举例说明。
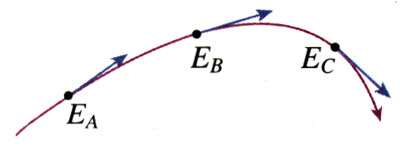
5.图1.3-11是某区域的电场线分布。A、B、C是电场中的三个点。
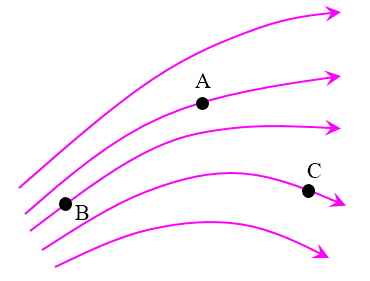
(1)哪一点电场最强,哪一点电场最弱?
(2)画出各点场强的方向。
(3)把负的点电荷分别放在这三点,画出所受静电力的方向。
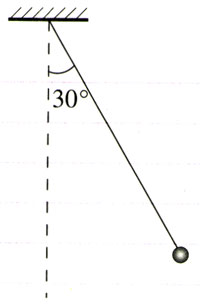
6.用一条绝缘轻绳悬挂一个带电小球,小球质量为1.0×10-2 kg,所带电荷量为+2.0×10-8 C。现加一水平方向的匀强电场,平衡时绝缘绳与铅垂线成30°(图1.3 -12)。求这个匀强电场的电场强度。
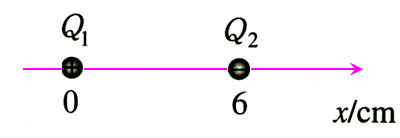
7.如图1.3-13,真空中有两个点电荷Q1=+4.0×10-8 C和Q2=-1.0×10-8 C,分别固定在x坐标轴的x=0和x=6cm的位置上。
(1)x坐标轴上哪个位置的电场强度为零?
(2)x坐标轴上哪些地方的电场强度方向是沿x方向的?
[1] 牛每库和伏每米两个单位间的换算关系,将在本章第六节谈到。
[2] 一般情况下用q或Q表示电荷量时,它们可能代表正电荷,也可能代表负电荷,正号或负号写在数值的前面。如q1=2×10-7 C代表一个负电荷,而q2=2×10-7 C或q2=+2×10-7 C代表一个正电荷。字母q或Q前面不再出现正负号。但有的时候字母前面加写正负号,目的是强调电荷的正负。
发布时间:2017/3/27 下午9:43:19 阅读次数:8495
