第十七章 5 不确定性关系

不确定性关系

我们再来考虑光的单缝衍射实验。

如果光子是经典的粒子，它在从光源飞向屏的过程中不受力的作用，应该做匀速直线运动，它在屏上的落点应该在缝的投影之内，如图17.5-1甲。但是，由于衍射，它到达屏上的位置会超出单缝投影的范围（图17.5-1乙）。由于其他粒子也具有波动性，所以其他粒子经过单缝时也有同样的现象。这说明，微观粒子已经不再遵守牛顿运动定律！实际上，通过下面的分析马上就会看到，我们根本不能像必修物理中学习的那样，同时用质点的位置和动量（当时用的是速度）来描述微观粒子的运动！

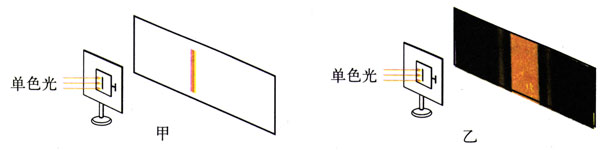
单缝衍射时，屏上各点的亮度反映了粒子到达这点的概率。如果把这个概率的分布在坐标系中表示出来，就是图17.5-2右侧的曲线。

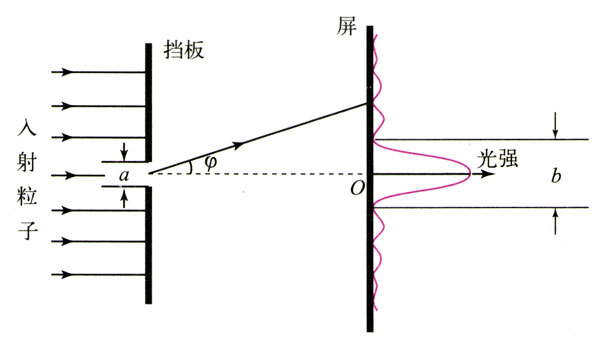
入射的粒子有确定的动量，但它们可以处于挡板左侧的任何位置，也就是说，粒子在挡板左侧的位置是完全不确定的。对于通过挡板狭缝的粒子则可以说，它们的位置被狭缝限定了，它们的位置不确定量减小了（不过我们仍然不能准确地说出射到屏上的粒子在通过狭缝时的准确位置，因为缝有一定的宽度a）。从下面的分析可以知道，粒子的动量的不确定量却增大了。

微观粒子具有波动性，会发生衍射，大部分粒子散布在宽度为b的中央亮条之内。这些粒子在到达狭缝之前沿水平方向运动，而在经过狭缝之后有些粒子跑到缝的投影位置以外，我们可以说这些粒子具有了与其原来运动方向垂直的动量。由于哪个粒子到达屏上的哪个位置完全是随机的，所以粒子在垂直方向上的动量也具有不确定性，不确定量的大小可以由中央亮条的宽度来衡量。

为了更准确地测定通过狭缝的粒子的位置，我们可以选用更窄的狭缝。但是，从衍射的规律可以知道，狭缝越窄，屏上中央亮条就越宽。这表明，尽管更窄的狭缝可以更准确地测得粒子的位置，但粒子动量的不确定量却更大了。

利用数学方法对微观粒子的运动进行分析可以知道，如果以Δx表示粒子位置的不确定量，以Δp表示粒子在x方向上的动量的不确定量，那么

ΔxΔp≥\(\frac{h}{{4\pi }}\)

式中h是普朗克常量。这就是著名的不确定性关系（uncertainty relation），简称不确定关系。

在经典物理学中，可以同时用质点的位置和动量精确地描述它的运动。不但如此，如果知道了质点的加速度，还可以预言质点在以后任意时刻的位置和动量，从而描绘它运动的轨迹。

但是，在微观物理学中，不确定关系告诉我们，如果要更准确地确定粒子的位置（即Δx更小），那么动量的测量一定会更不准确（即Δp更大），也就是说，不可能同时准确地知道粒子的位置和动量，因而也就不可能用“轨迹”来描述粒子的运动。

我们不可能准确地知道单个粒子的运动情况，但是我们可以准确地知道大量粒子运动时性的统计规律。一个宏观系统总是包含着大量粒子，因此我们仍然能够对宏观现象进行预言。例如，当粒子数很少时，我们不能预言粒子通过挡板上的狭缝后落在屏上的位置，但却可以准确地知道粒子落在屏上某点的概率；概率大的位置正好是某种波通过狭缝发生衍射时产生亮条的位置。

物理模型与物理现象

在经典物理学中，对于不同的宏观对象，我们分别建立了粒子模型和波动模型，它们与直接经验一致。然而，对于微观世界的属性，我们缺少直接感知。在这种情况下，我们也要设想一些模型，以分析和研究它们的规律，尽管以日常经验来衡量，这种模型的行为十分古怪。粒子的波粒二象性就是如此。以至于爱因斯坦说，这个任务对我们的想像力来说是力所不及的。但是，只要它与实验结果一致，它就能够在一定范围内正确代表研究的对象。

自然科学并不是自然本身，它是人类和自然关系的一部分。

——海森伯[1]

根据德布罗意提出的关系λ＝\(\frac{h}{p}\)，可以肯定地说，波动性是所有运动物体都具有的，不管是一个电子，还是一颗飞行的子弹，乃至一个星球……只不过子弹和星球的动量太大，波长要比原子和电子的波长小得多，因而难于观察到它们的波动图景。

在波粒二象性和不确定关系的基础上建立的量子力学被认为是一件科学的艺术品，它的预言与实验惊人地一致，而它的成功应用更是遍及现代社会的每个角落。没有量子力学就没有现代半导体材料。从电子表、电视机到核电站和计算机，无不留下量子的足迹。是量子力学引领我们迈入了现代社会，让我们享受到丰富多彩的现代生活。

但是，对于“量子”的图景和哲学意义，却一直存在着严重的分歧和激烈的争论。

作为20世纪最伟大的物理学家之一，爱因斯坦对量子理论的思索比对相对论的考虑要多得多。即便如此，他在晚年也只好承认：“整整50年有意识的思考，并没有使我更接近‘光量子是什么’这个问题的答案。”

然而，越困难、越具有挑战性的问题，就越让人类的好奇心无法割舍。这种思考和争论仍在继续着……

科学漫步

量子力学

量子力学是关于微观粒子运动规律的基本理论。微观粒子表现出一系列不同于宏观颗粒的性质，根本之点在于微观粒子具有波粒二象性，从而它所遵从的物理规律也与宏观物体根本不同。在量子力学建立之前，N．玻尔曾根据普朗克、爱因斯坦等提出的量子概念建立了前期量子论，可以部分地说明原子的若干性质。然而这个理论能够解决的问题有限，而且理论中还存在不和谐因素。这些都不能令人满意。1925年，海森伯等人着眼于对前期量子论的批判，发展了矩阵力学；1926年，薛定谔根据德布罗意的波粒二象性假说建立了波动力学。不久，薛定谔等人证明矩阵力学与波动力学在数学上是等价的，于是两种理论融合为量子力学。以后又由于狄拉克等人的进一步发展，量子力学成为逻辑严谨、方法齐备的崭新理论。

量子力学与经典力学有根本的差别。量子力学中，粒子的状态用波函数ψ（r，t）描述，它是坐标r和时间t的复数函数。波函数的模的二次方|ψ（r，t）|²表示在时刻t、坐标为r的位置找到粒子的概率密度。在粒子速度不太大的非相对论情况下，粒子状态随时间变化的规律，即波函数所满足的运动方程是薛定谔方程；在粒子速度很大的相对论情况下，薛定谔方程由狄拉克方程或克莱因-戈尔登方程所取代。

玻尔关于氢原子能级的概念可以自然地从量子力学推出，而不再是人为的假设。不但如此，量子力学在原子、分子、固体以及微观粒子的碰撞等众多问题上，都得到了与实验符合得很好的结果，获得了极大的成功。

量子力学后来又有了发展。在高能情形下，粒子的转变是一种普遍现象，所有粒子，包括光子、电子、介子、核子等，必须用统一的方式处理，这样才能把粒子的产生、湮没和转化反映到理论中去。为了这种需要，在量子力学的基础上出现了量子场论。量子场论已经成为粒子物理、统计物理、凝聚态物理和核物理的基本理论工具。

问题与练习

1．请举一个例子说明：在经典物理学中，我们可以同时确定物体的位置和动量。

2．请举一个例子说明：在微观物理学中，粒子的位置和动量具有不确定关系。这时，牛顿运动定律还成立吗？

3．有人说：“在微观物理学中，由于我们不可能同时准确地知道某个粒子的位置和动量，粒子出现的位置是无规律可循的。”请你对以上说法做出评论。

4．在光的单缝衍射实验中，狭缝变窄，光子动量的不确定量如何变化？请用实验现象解释这个结论。

发布时间：2017/3/21 下午2:18:30  阅读次数：2196