第十九章 5 核力与结合能

中子和质子构成原子核的模型提出以后，有一个问题当时未能得到合理的解释——在原子核那样狭小的空间里，带正电的质子为什么能挤在一起而不飞散？

核力与四种基本相互作用

20世纪初，人们只知道自然界存在着两种力：一种是万有引力，另一种是电磁力。对于带电粒子，在相同的距离上这两种力的强度差别很大，电磁力大约要比万有引力强10³⁵倍。

基于这两种力的性质，原子核中的质子要靠自身的万有引力来抗衡相互间的库仑斥力是不可能的。核物理学家猜想，原子核里的核子间有第三种相互作用存在，即存在着一种核力，是核力把核子紧紧地束缚在核内，形成稳定的原子核。后来的实验证实了科学家的猜测，并进一步揭示了核力的以下特点。

（1）核力是强相互作用（强力）的一种表现。在原子核的尺度内，核力比库仑力大得多。

（2）核力是短程力，作用范围在1.5×10^-15 m之内。核力在大于0.8×10^-15 m时表现为吸引力，且随距离增大而减小，超过1.5×10^-15 m，核力急剧下降几乎消失；而在距离小于0.8×10^-15 m时，核力表现为斥力，因此核子不会融合在一起。

（3）每个核子只跟邻近的核子发生核力作用，这种性质称为核力的饱和性。

然而，直到今日，人们对核力的了解还很不够，特别是在小于0.8×10^-15 m时核力的变化规律还不清楚。这些是科学家们正在奋力攻克的堡垒。

除核力外，核物理学家还在原子核内发现了自然界的第四种相互作用——弱相互作用（弱力），弱相互作用是引起原子核β衰变的原因，即引起中子-质子转变的原因。弱相互作用也是短程力，其力程比强力更短，为10^-18 m，作用强度则比电磁力小。

物理学家一直梦想将自然界中的四种相互作用纳入某种统一的理论之中。爱因斯坦为此做了大半生的努力，但没有成功。1967年，温伯格（S．Weinberg）和萨拉姆（A．Salam）在格拉肖（S．Glashow）电弱统一模型的基础上提出了电弱统一的完善理论。他们三人因此获得了1979年的诺贝尔物理学奖。

原子核中质子与中子的比例

大家已经知道，一个质子与一个中子结合在一起是氢的一种同位素——氘。两对质子-中子相结合就是氦，8对质子-中子的结合是氧。这些都是自然界中存在的原子核。那么，这样质子数与中子数相等的结构，能够形成很大的原子核吗？不会的。从图19.5-2看出，自然界中较轻的原子核，质子数与中子数大玫相等，但对于较重的原子核，中子数大于质子数，越重的元素，两者相差越多。

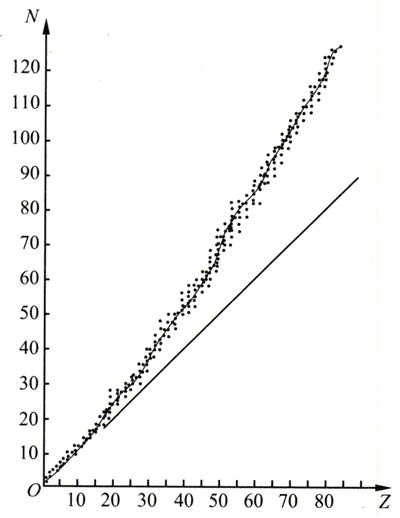
这个现象能够用核力与电磁力的不同特点来解释。

可以设想，我们把质子与中子成对地放在一起，人工构建原子核，它的质子数与中子数相等。人工核越来越大，有些核子间的距离越来越远。随着距离的增加，核力与电磁力都会减小，但核力减小得更快。所以，原子核大到一定程度时，相距较远的质子间的核力不足以平衡它们之间的库仑力，这个原子核就不稳定了。这时，如果不再成对地增加质子和中子，而只增加中子，中子与其他核子没有库仑斥力，但有相互吸引的核力，所以有助于维系原子核的稳定。由于这个原因，稳定的重原子核里，中子数要比质子数多。由于核力的作用范围是有限的，以及核力的饱和性，如果我们继续增大原子核，一些核子间的距离会大到其间根本没有核力的作用，这时即使再增加中子，形成的核也一定是不稳定的。

在宇宙演化的进程中，各种粒子有机会进行各种组合，但那些不稳定的组合逐渐瓦解了，只有200多种稳定的原子核长久地留了下来。

结合能

我们考虑下面的问题。相距很远的两个物体，由于万有引力而相互接近，运动速度越来越大，引力势能转化为动能。最后撞在一起，动能变成它们的内能散失掉了。两个物体为了结合而付出了代价——失去了一些能量，如果要把它们分开，还要重新赋予它们这份能量。

这是用宏观物体做的一个例子。原子核是核子结合在一起构成的，要把它们分开，也需要能量，这就是原子核的结合能（binding energy）。

其实我们还遇到过其他类似的例子。要使基态氢原子电离，也就是要从氢原子中把电子剥离，需要通过碰撞、施加电场、让氢原子吸收光子等途径使它得到13.6 eV的能量。这个能量实际上就是电子与氢原子核的结合能，不过通常把它叫做氢原子的电离能，而结合能一词只用在原子核中。

自然，原子核越大，它的结合能越高。因此，有意义的是它的结合能与核子数之比，称做比结合能（specific binding energy），也叫平均结合能。比结合能越大，表示原子核中核子结合得越牢固，原子核越稳定。

质量亏损

原子核的结合能很难直接测量。幸好，爱因斯坦已经给我们指出了物体的能量与它的质量的关系，即

E＝mc²

单个的质子、中子的质量已经精确测定。用质谱仪或其他仪器测定某种原子核的质量，与同等数量的质子、中子的质量之和相比较，看一看两条途径得到的质量之差，就能推知原子核的结合能。

【例题】已知中子的质量是m_n＝1.674 9×10^-27 kg，质子的质量是m_p＝1.672 6×10^-27 kg，氘核的质量是m_D＝3.343 6×10^-27 kg，求氘核的比结合能。

【解】单个的质子与中子的质量之和为

m_p＋m_n＝（1.672 6＋1.674 9）×10^-27 kg＝3.347 5×10^-27 kg

这个数值与氘核质量之差

（m_p＋m_n）－m_D＝（3.347 5- 3.343 6）×10^-27 kg＝0.003 9×10^-27 kg

与这个质量差相对应的能量为

ΔE＝Δmc²＝0.003 9×10^-27×（3.00×10⁸）² J＝3.51×10^-13 J

在核物理中，能量单位常常使用电子伏特：1 eV＝1.60×10^-19 J，所以，氘核的结合能是

ΔE＝\(\frac{{3.51 \times {{10}^{ - 13}}}}{{1.60 \times {{10}^{ - 19}}}}\)eV＝2.19×10⁶ eV＝2.19 MeV

氘核的比结合能为

\(\frac{{2.19{\rm{MeV}}}}{2}\)＝1.10 MeV

通过这个例题可以看出，原子核的质量小于组成它的核子的质量之和，这个现象叫做质量亏损（mass defect）。质量亏损表明，的确存在着原子核的结合能。

不同原子核的比结合能是不一样的，图19.5-3是按照实际测量结果所画的图线。可以看出：中等大小的核的比结合能最大（平均每个核子的质量亏损最大），这些核最稳定。

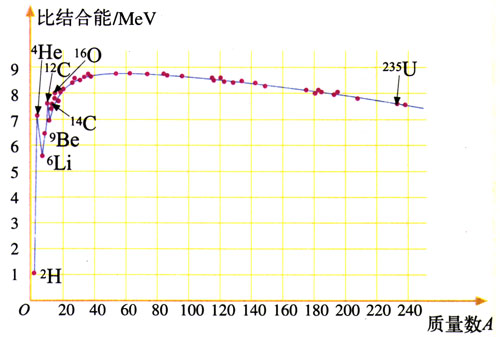
这个现象在20世纪20年代末曾经引起遐想：如果使较重的核分裂成中等大小的核，或者把较小的核合并成中等大小的核，核子的比结合能都会增加，这样岂不是可以释放能量供人使用？

前景的确诱人，但是怎样使原子核发生分裂或者合并呢？这在当时是一个无法解决的问题。

问题与练习

1．从以下几个方面比较核反应与化学反应的相同和相异之处。

（1）它们各自涉及四种基本力中的哪一种？

（2）每种反应分别改变了或重新安排了什么？

2．通常我们看到物体的铯量发生变化时，为什么觉察不到物体质量发生的变化？

3．碳原子质量的\(\frac{1}{{12}}\)叫做原子质量单位，用u表示。请根据E＝mc²证明：1u相当于931 MeV。

4．印刷“两弹一星”这四个字的油墨的质量大约是1 μg（10^-9 kg）。与这些质量相当的能量如果完全用来增加重力势能，它可以使一架本身质量6 000 kg，载有60名体重50 kg学生的直升机升到多高？

发布时间：2017/3/7 上午8:54:00  阅读次数：4679