第十一章 4 单摆
生活中经常可以看到悬挂起来的物体在竖直平面内摆动,我们用细线悬挂着的小球来研究摆动的规律。
如图11.4-1,如果细线的质量与小球相比可以忽略;球的直径与线的长度相比也可以忽略,这样的装置就叫做单摆(simple pendulum)。单摆是实际摆的理想化模型。显然,单摆摆动时摆球在做振动,但它是不是在做简谐运动?
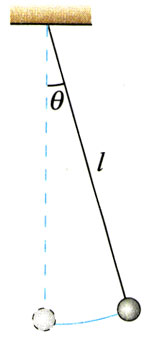
研究单摆时还有一个条件:与小球受到的重力及绳的拉力相比,空气等对它的阻力可以忽略。
为了更好地满足这个条件,实验时我们总要尽量选择质量大、体积小的球和尽量细的线。
演示
如图11.4-2,细线下悬挂一个除去了柱塞的注射器,注射器向下喷出一细束墨水。沿着与摆动方向垂直的方向匀速拖动一张白纸,白纸上的墨迹便画出振动图象(x-t图象)。
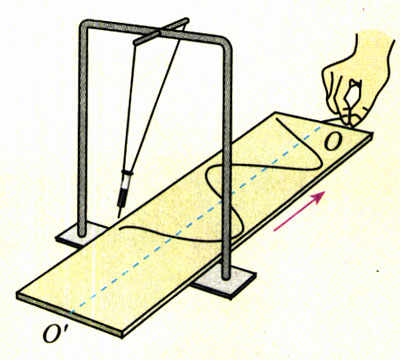
注射器的摆动是不是简谐运动?
单摆的回复力
我们在一般条件下研究单摆是不是做简谐运动,最简单的方法是看它的回复力是否满足F=-kx的条件。
摆球静止在O点时,悬线竖直下垂,摆球受到的重力G与悬线的拉力Fʹ平衡。小球受的合力为零,可以保持静止,所以O点是单摆的平衡位置。拉开摆球,使它偏离平衡位置,放手后摆球所受的重力G与拉力Fʹ不再平衡。在这两个力的合力的作用下,摆球沿着以平衡位置O为中心的一段圆弧AAʹ做往复运动,这就是单摆的振动。
因为摆球沿圆弧运动,因此可以不考虑沿悬线方向的力,只考虑沿圆弧方向的力。当摆球运动到某点P时(图11.4-3),摆球在圆弧方向上受到的只是重力在这个方向的分力F=mgsinθ,这就是它的回复力。
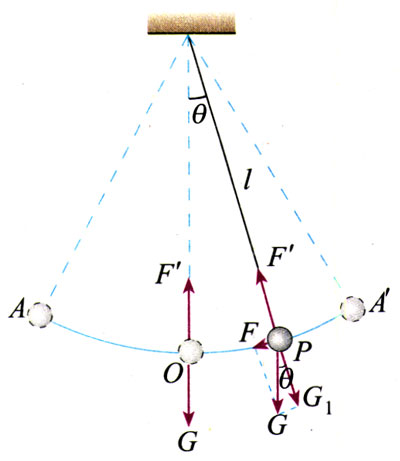
在偏角很小时,摆球对于O点的位移x的大小,与θ角所对的弧长、θ角所对的弦都近似相等,因而sinθ≈\(\frac{{x}}{l}\),所以单摆的回复力为
F=-\(\frac{{mg}}{l}\)x
其中l为摆长,x为摆球偏离平衡位置的位移,负号表示回复力F与位移x的方向相反。由于m、g、l都有确定的数值,\(\frac{{mg}}{l}\)可以用一个常数k表示,于是上式写成
F=-kx
可见,在偏角很小的情况下,摆球所受的回复力与它偏离平衡位置的位移成正比,方向总是指向平衡位置,因此单摆做简谐运动。
当角θ很小时,用弧度表示时θ与它的正弦sinθ近似相等;θ所对的弦长与它所对的弧长也近似相等。这两个关系的严格证明要用到高等数学,本书不做讨论。
单摆的周期
一条短绳系一个小球,它的振动周期很短,天文馆里巨大的傅科摆,周期很长。单摆的周期与什么因素有关?

演示
单摆的振幅、质量、摆长对周期各有什么影响?
如图11.4-4,在铁架台的横梁上固定两个单摆,按照以下几种情况,把它们拉起一定角度后同时释放,观察两摆的振动周期。
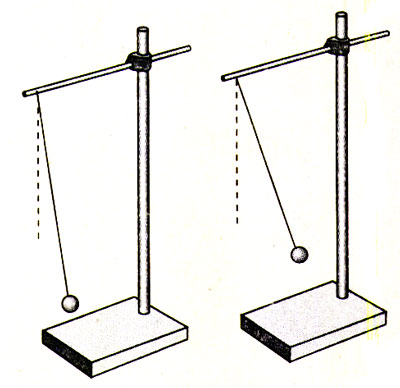
1.两摆的振幅不同(都在小偏角下)
2.两摆的质量不同
3.两摆的摆长不同
比较三种情况下两摆的周期,可以得出什么结论?
实验表明:单摆振动的周期与摆球质量无关,在振幅较小时与振幅无关,但与摆长有关,摆长越长,周期也越长。
单摆周期与摆长之间有什么定量的关系?
实验
探究单摆周期与摆长的关系
如图11.4-5,细线的上端固定在铁架台上,下端系一个小钢球,于是做成了一个单摆。测量摆长和摆的周期,得到一组数据;改变摆长,再得到几组数据。从中可以找出周期与摆长的关系。
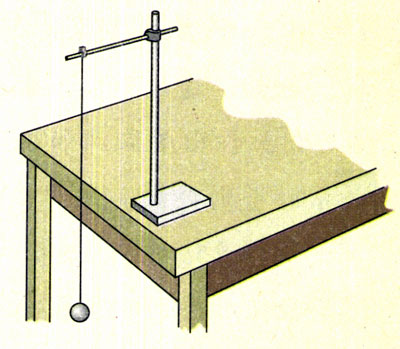
实验过程中要注意以下几点。
1.摆的振幅不要太大
前面的分析中利用了一些近似条件,这些近似只有当摆的振幅不大时才能成立,否则摆的振动不是简谐运动,周期与摆长的关系将会十分复杂。
2.摆线和摆球的选择
摆线要尽量选择细些的、伸缩性小些的,并且要尽可能长一些。摆球要尽量选择质量大些的、体积小些的。
为什么这样做?
3.细线上端的悬挂方式
图11.4-6甲、乙两图画出了细线上端的两种不同的悬挂方式。哪种较好?为什么?
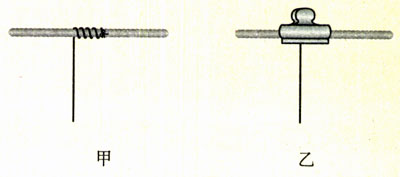
4.摆长的测量
可以用刻度尺测量细线的长度,用游标卡尺测量小球的直径,算出它的半径,两者之和作为摆长的测量值。
5.周期测量的要点
按下停表开始计时,再按下停表计时终止。为了测量周期,摆球到达哪个位置的时刻作为计时开始与停止的时刻比较好?图11.4-7给出了两个选择。你选择哪个?说出道理。

图11.4-7 哪个位置作为计时的开始与终止更好些?
可以测量单摆做一次全振动的时间作为它的周期的测量值;也可以测量单摆做多次全振动(例如几十次)的时间,然后通过计算求出它的周期的测量值。哪个方法比较好?为什么?
选择摆线长度和测量摆的周期时,都要考虑到测量的绝对误差和相对误差,建议复习《必修l》后面“学生实验”中的相关知识。
6.数据分析
先通过数据分析,对周期T与摆长l的定量关系做出猜测,例如可能是T∝l、T∝l2,或者T∝\(\sqrt l \)、T∝\(\sqrt[3]{l}\)……然后按照猜测来确定纵坐标轴和横坐标轴。例如,通过估算我们认为可能是T∝l2,那么可以用纵坐标表示T,横坐标表示l2,作出图象。如果这样作出的图象确实是一条直线,说明的确有T∝l2的关系,否则再做其他尝试。
设计表格时要注意,表中一定要有原始记录。例如,摆长是由细线长度与小球半径相加得到的,表中不能只出现摆长,一定要有细线长度和球的直径的测量值的记载。
建议在计算机上用数表软件处理数据,这样节省时间,效果又好。
荷兰物理学家惠更斯曾经详尽地研究过单摆的振动,发现单摆做简谐运动的周期T与摆长l的二次方根成正比,与重力加速度g的二次方根成反比,而与振幅、摆球质量无关。惠更斯确定了计算单摆周期的公式[1]
T=2π\(\sqrt {\frac{l}{g}} \)

用单摆测定重力加速度
由单摆周期公式可得g=\(\frac{{4{\pi ^2}l}}{{{T^2}}}\),如果测出单摆的摆长l、周期T,就可以求出当地的重力加速度。
我们在图11.4-5的实验中已经获得了摆长和周期的实验数据,可以从中选择几组,分别计算重力加速度,然后取平均值。
除了计算平均值外,还可以分别以l和T2为纵坐标和横坐标,作出函数l=\(\frac{g}{{4{\pi ^2}}}\)T2的图象,它应该是一条直线。根据这条直线的倾斜程度求出\(\frac{g}{{4{\pi ^2}}}\),进而求出重力加速度g。
问题与练习
1.一个理想的单摆,已知其周期为T。如果由于某种原因(如转移到其他星球)自由落体加速度变为原来的\(\frac{1}{2}\),振幅变为原来的\(\frac{1}{3}\),摆长变为原来的\(\frac{1}{4}\),摆球质量变为原来的\(\frac{1}{5}\),它的周期变为多少?
2.周期是2s的单摆叫做秒摆,秒摆的摆长是多少?把一个地球上的秒摆拿到月球上去,已知月球上的自由落体加速度为1.6m/s2,它在月球上做50次全振动要用多少时间?
3.图11.4-8是两个单摆的振动图象。
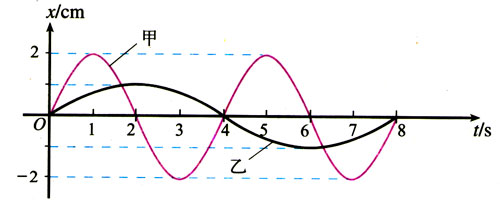
(1)甲、乙两个摆的摆长之比是多少?
(2)以向右的方向作为摆球偏离平衡位置的位移的正方向,从t=0起,乙第一次到达右方最大位移时,甲振动到了什么位置?向什么方向运动?
4.一条细线下面挂一个小球,让它自由摆动,作出它的振动图象如图11.4-9。问:
(1)你能根据图中的数据算出它的摆长吗?
(2)你能根据图中的数据估算它摆动的最大偏角吗?
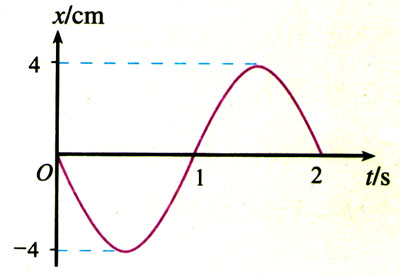
[1] 利用高等数学研究单摆的运动就会看到,该式是个近似公式,由它算出的周期与精确值之间的差别随着偏角的增加而增加。当偏角为5°时两者相差0.01%,7°时相差0.1%,15°时相差0.5%,23°时相差1%。
发布时间:2017/1/6 下午10:57:04 阅读次数:7521
