第2章 五、气体的压强跟体积的关系

我们知道气体分子间的平均距离很大，所以一定质量气体的体积很容易改变。作为动力使用的压缩空气就是把一定质量的空气的体积压缩得很小，使它具有很大的压强，通常可达6×10⁵～8×10⁵帕（相当于大气压强的6～8倍），本章导图1中，建筑工人清理地基使用的风镐，就是利用压缩空气作为动力的。钢笔吸墨水是利用钢笔里的橡皮管恢复原状时，它里面存留的空气体积变大，压强随着变小，墨水就被吸入橡皮管内。

日常生活中还会见到如图2-17所示的一些现象，好像空气是具有“弹性”的。其实这都表明气体的压强跟体积有关。

玻意耳定律

注意到气体压强随体积变化而变化的事实，并首先进行定量研究的是英国科学家玻意耳（1627-1691）。

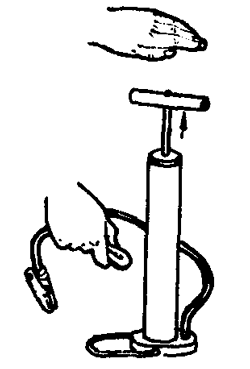
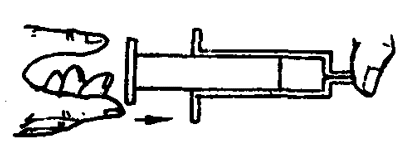
1662年，玻意耳用水银把空气封闭在很长的J形玻璃管的短臂内进行实验。设法调节封在短臂内的空气，使管子竖直放置时，J形管两臂内的水银面在同一高度上[图2-18（a）]。这时，封闭在管内的空气压强等于当时的大气压强。由于玻璃管内径均匀，管内空气体积便可由空气柱的长度来表示。

玻意耳采用在J形管长臂内注入更多水银的方法来增大短臂内空气的压强，他发现当J形管长臂内的水银面高于短臂内的水银面时，短臂内的空气柱长度变短了，这表明空气被压缩时，空气体积减小的同时，压强在增大。他又注意到用湿布揩拭短臂或晚间照明的烛焰靠近短臂时，短臂内空气柱的体积都会发生变化。这就提醒了玻意耳，在整个实验过程中，空气柱的温度必须保持不变，只有这样，才能找出只由于压强变化所引起的空气体积变化的规律。

因此，玻意耳设法使实验在温度保持不变的条件下进行。他发现当短臂内的室气柱体积被压缩一半时，长臂内的水银面比短臂内的水银面高出760毫米（760毫米水银柱产生的压强约等于大气压强）。这就是说，当短臂内的空气的压强增大到等于大气压强的2倍时，空气的体积减小为原来的1/2[图2-18 （b）]。

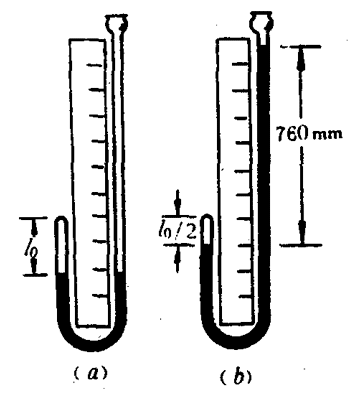
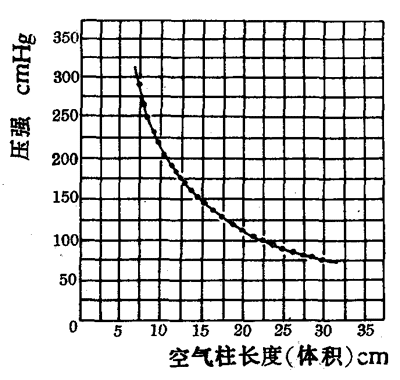
图2-19是根据玻意耳实验的原始数据描绘的压强-体积图象（p-V图象）。图中以直角坐标系的纵轴表示J形管短臂内空气压强p（其大小等于外加于这部分空气的压强），单位用水银柱高度cmHg[1]来表示；横轴表示空气体积V，用空气柱长度的厘米数表示（因管内空气柱粗细均匀，所以可用空气柱的长度来表示空气柱的体积），单位用cm。由图象可以看出这是一段等轴双曲线，它表明

一定质量气体在温度不变时，它的压强跟体积成反比。这一实验结论叫做玻意耳定律。

若气体压强用p表示，体积用V表示，玻意耳定律可用以下公式表示

p₁V₁＝p₂V₂，

或    pV＝C（常数）。

运用玻意耳定律解决实际问题时，应注意这样几点：

1．认清被研究的对象是哪部分气体，这部分气体的质量必须是一定的；

2．它只能在温度不变的条件下适用；

3．要分清气体状态变化前、后的压强和体积；

4．气体状态变化前、后，压强和体积必须分别用同一单位。

等温过程的获得

在研究一定质量的气体的压强和体积的关系时，必须控制温度保持不变，这样的过程叫做等温过程。例如将被研究的气体放在大量冰水混和物中被压缩、体积减小时，外界对这部分气体做功，气体的温度将升高，这就不是一个等温过程，但是，如果压缩过程很缓慢，则这部分气体可以及时向周围的冰水混和物放热，使0℃的冰逐步熔化一部分，而气体温度始终保持在0℃。相反，当气体体积增大、气体对外做功时，温度将降低，这也不是一个等温过程。但是，如果膨胀过程很缓慢，则这时气体也可以从周围冰水混和物中及时吸收热量，使部分0℃的水逐渐凝固成冰，而气体温度始终保持在0℃。所以为了让气体来得及跟周围物质进行热交换，以使它的温度保持不变，等温过程必须进行得十分缓慢。

在其他温度下（不一定是0℃）做实验，要使气体经历一个等温过程，首先必须使环境温度保持不变。

【例题1】

一个体积为V的沼气泡自池塘底浮起，若水深为3米，沼气泡从池底上升到水面时，它的体积将变为原来的多少倍（图2-20）？（设水底和水面温度相同，大气压强为1.0×10⁵帕。）

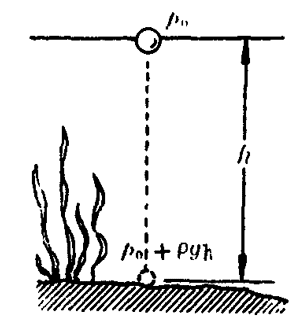
【解】沼气泡在池底时，气泡内的气体压强等于大气压强和池水产生的压强之和，即p₁＝p₀＋ρgh，设这时气泡内气体体积为V₁＝V。当气泡上升到水面时，气泡内气体压强p₂＝p₀，体积为V₂。根据玻意耳定律p₁V₁＝p₂V₂，得

V₂＝\(\frac{{{p_1}{V_1}}}{{{p_2}}}\)＝\(\frac{{({p_0} + \rho gh)V}}{{{p_0}}}\)＝\(\frac{{(1.0 \times {{10}^5} + 1.0 \times {{10}^3} \times 9.8 \times 3)}}{{1.0 \times {{10}^5}}}\)V＝1.29V。

即气泡上升到水面时，体积扩大为原来体积的1.29倍。

【例题2】

一端封闭的、足够长的均匀直玻璃管内有一段长3厘米的水银，当玻璃管水平放置时，封闭在管内的空气柱长5厘米[图2-21（a）]。如果小心地将这根玻璃管竖立起来，并使开口的一端向下[图2-21（b）]，这时管内空气柱的长度是多少？（设温度保持不变，大气的压强为1. 0×10⁵帕，水银的密度为13.6×10³千克/米³。）

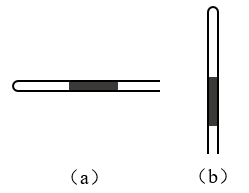
【解】玻璃管水平放置时，管内空气柱的压强等于大气压强，即p₁＝p₀，因玻璃管内径均匀，设空气柱截面积为a米²，则空气柱体积V₁＝l₁a。当玻璃管开口的一端向下竖直放置时，管内空气压强将减小为p₂，p₂＝p₀－ρgh。根据玻意耳定律p₁V₁＝p₂V₂，得

V₂＝\(\frac{{{p_1}{V_1}}}{{{p_2}}}\)＝\(\frac{{{p_0} \cdot {l_1}a}}{{{p_0} - \rho gh}}\)＝\(\frac{{1.0 \times {{10}^5} \times 5 \times {{10}^{ - 2}}a}}{{1.0 \times {{10}^5} - 13.6 \times {{10}^3} \times 9.8 \times 3 \times {{10}^{ - 2}}}}\)米²＝0.052a米³，

管内空气柱长度

l₂＝\(\frac{{{V_2}}}{a}\)＝\(\frac{{0.052a}}{a}\)米＝0.052米＝5.2厘米。

思考

1．请你解释图2-17所示的空气具有“弹性”的现象。

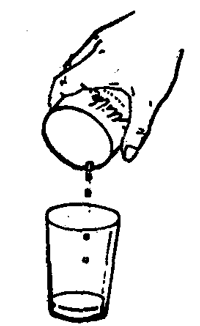
2．罐装牛奶是密封的，如果只在罐子顶部开一个小孔，牛奶很难从小孔倒出（图2-22），这是什么原因？

问题探讨

S（学生）：将一根两端开口的玻璃管竖直插入水中，用手指紧紧按住露出水面一端的管口，然后将玻璃管向上提起几厘米，这时管中的水面为什么会比管外水面高一些，而又比玻璃管向上提起的高度小？应当怎样来分析这个问题呢？

T（教师）：首先，管中的液面不可能一点也不上升，否则管内、外液面持平，被封闭在管内的空气柱压强不变，而体积却增大了，这是不可能的；其次，管中的液面上升的高度也不可能跟玻璃管上提的高度相等，否则，空气柱的体积不变，而压强却小于原来的大气压强了，这同样也是不符合玻意耳定律的。只有管内水面比管外水面高一些，又比玻璃管向上提起的高度小一些，管中空气体积增大、压强减小才符合玻意耳定律。由此可见，分析这类体积变化问题的同时，还要分析气体压强的变化。

练习六

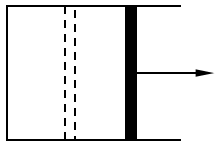
1．如图2-23所示，带有活塞的容器内有一定质量的气体，已知气体压强为1.0×10⁵帕，体积为2升。如果在外力作用下，将活寒向右拉动，使容器内的气体体积增大到4升，则容器内气体的压强将变为多大？如果不计活塞与器壁间的摩擦，活塞的截面积为100厘米²，为了使活塞平衡，这时需用多大的拉力？（设温度保持不变，大气压强为1.0×10⁵帕。）

2．如果上题中的已知条件是：原来气体的压强为1.0×10⁵帕，密度为1.29千克/米³。在外力作用下，十分缓慢地将活塞向左推动，当容器里气体的压强达到5×10⁵帕时，容器里气体的密度将是多大？

3．这里介绍一种简单的测定大气压强的实验方法：在一端封闭的均匀直玻璃管中，用一段水银封住一定量的空气，当玻璃管开口端向上竖直放置时[图2-24（a）]，测得水银柱高度为h，空气柱长度为l₁。小心地把玻璃管放成水平，测得空气柱长度为l₂[图2-24（b）]。设温度保持不变，水银密度为ρ，根据上面的数据，试写出大气压强p₀的表达式。

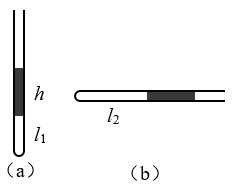
如果仍用这根装有一段水银柱的玻璃管，将开口端向下竖直放置，是否也能测出大气压强？

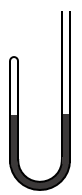
4．如图2-25所示，一端开口、一端封闭的均匀U形管内盛有水银，左臂内封有一定质量的空气，当U形管竖直放置时，两臂内的水银面在同一高度；现从开口的一端再灌入一些水银，使两臂内水银面的高度差为2厘米，左臂内的空气被压缩1厘米，求左臂内原来的空气柱长。（设温度不变，大气压强为1.0×10⁵帕。）

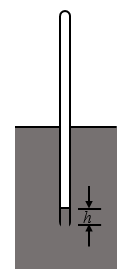
5．将一根长1米、一端封闭的均匀玻璃管开口的一端竖直地向下插入水中，当把玻璃管的一半长度插入水中时，进入玻璃管中的水柱高度h为多大（图2-26）？（设温度保持不变，大气压强为1.0×10⁵帕。）

发布时间：2016/11/9 上午10:59:42  阅读次数：7673