第五章1 曲线运动

力学是关于运动的科学，它的任务是以完备而又简单的方式描述自然界中发生的运动。

——基尔霍夫[1]

到目前为止，我们只研究了物体沿着一条直线的运动。实际上，在自然界和技术中，曲线运动随处可见。水平抛出的物体，在落到地面的过程中沿曲线运动；地球绕太阳公转，轨迹接近圆，也是曲线。抛出的物体、公转中的地球，它们的运动都是曲线运动（curvilinear motion）。

从现在开始，我们把目光转向抛体运动、圆周运动，以及更一般的曲线运动，从中你会看到，我们研究直线运动时的思路，原则上同样可以用来处理曲线运动。

通过本章和下一章的学习，你还会发现：地球上物体的运动和天体的运动原来遵从同样的科学规律！'

1 曲线运动

从现在开始，我们研究质点沿曲线运动时所遵循的规律。这一节的任务是找出描述曲线运动的方法，下一节将根据牛顿运动定律得出质点做曲线运动的规律。这个思路与研究直线运动时是一样的。

描述直线运动时要用到位移和速度两个物理量，描述曲线运动时也是这样。

曲线运动的位移

研究物体的运动时，坐标系的选取是很重要的。例如我们把一个物体沿水平方向抛出，它不会一直在水平方向上运动，而是沿着一条曲线落向地面。这种情况下无法应用直线坐标系，而应该选择平面直角坐标系。例如，这个坐标系的原点可以选在物体离开手掌时的位置，同时让x轴沿水平抛出的方向、y轴沿竖直向下的方向，如图5.1-1。

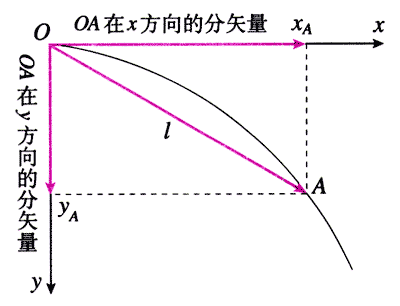
当物体运动到A点时，它相对于抛出点的位移是OA，可以用l表示。然而这类问题中位移矢量l的方向在不断变化，运算不太方便，所以要尽量用它在坐标轴方向的分矢量来代表它。由于两个分矢量的方向是确定的，所以只用A点的坐标x_A、y_A就能表示它们，于是问题就简单些了。

过去建立平面直角坐标系时总使y轴的方向朝上，其实朝下也是可以的。但这时要注意，处于x轴下方的点的纵坐标不是负值而是正值。

思考与讨论

观察图5.1-2、图5.1-3描述的现象，你能不能说清楚，砂轮打磨下来的炽热微粒、飞出去的链球，分别沿着什么方向运动？

曲线运动的速度

运动员掷链球时，链球在手的牵引下做曲线运动，一旦运动员放手，链球即刻飞出。放手的时刻不同，链球飞出的方向也不一样，可见做曲线运动的物体，不同时刻的速度具有不同的方向。所以，在研究曲线运动的速度时，我们首先考虑怎样确定物体在某一时刻的速度的方向。

演示

如图5.1-4，水平桌面上摆一条弯曲的轨道，它是由几段稍短的弧形轨道组合而成的。通过压缩弹簧或者斜面使钢球由轨道的C端滚入，在轨道的约束下做曲线运动。在轨道的下面放一张白纸，蘸有墨水的钢球从出口A离开轨道后在白纸上留下一条运动的痕迹，它记录了钢球在A点的运动方向。

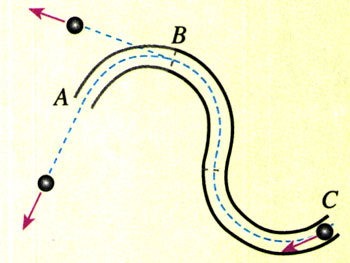
拆去一段轨道，钢球的轨道出口改在B。用同样的方法可以记录钢球在轨道B点的运动方向。

白纸上的墨迹与轨道（曲线）有什么关系？

讨论曲线运动的速度方向时要明确一个数学概念：曲线的切线。在初中数学里我们已经知道圆的切线，对于其他曲线，切线指的是什么？

如图5.1-5，过曲线上的A、B两点作直线，这条直线叫做曲线的割线。设想B点逐渐向A点移动，这条割线的位置也就不断变化。当B点非常非常接近A点时，这条割线就叫做曲线在A点的切线（tangent）。

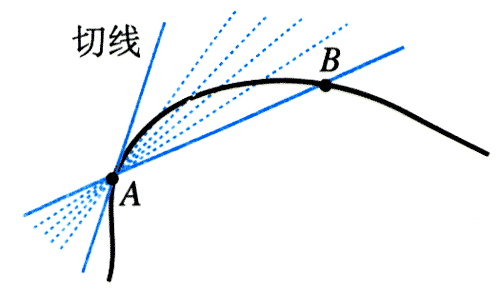
有了切线的概念，我们就可以说：质点在某一点的速度，沿曲线在这一点的切线方向。

速度是矢量，它既有大小，又有方向。不论速度的大小是否改变，只要速度的方向发生改变，就表示速度矢量发生了变化，也就有了加速度。曲线运动中速度的方向在变，所以曲线运动是变速运动。

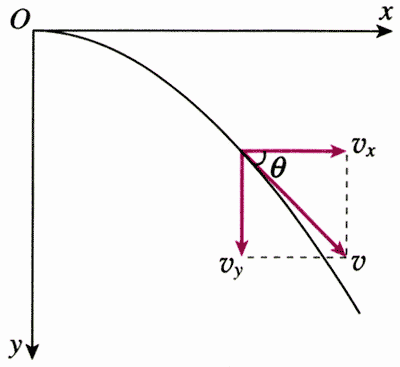
速度是矢量，它与力、位移等其他矢量一样，可以用它在相互垂直的两个方向的分矢量来表示，这两个分矢量叫做分速度。我们仍以被抛出的物体的运动为例（图5.1-6）。物体的速度记做v，沿曲线的切线方向，v_x、v_y是它在两个坐标轴方向的分速度。如果速度方向与x轴的夹角是θ，按照锐角三角函数的定义，两个分速度v_x、v_y与速度v的关系是

v_x＝vcos θ

v_y＝vsin θ

例题

飞机起飞时以300 km/h的速度斜向上飞，飞行方向与水平面的夹角为30º。求水平方向的分速度v_x和竖直方向的分速度v_y。

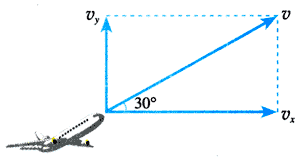
解  把速度v＝300 km/h按水平方向和竖直方向分解，如图5.1-7，可得

v_x＝vcos 30º＝260 km/h

v_y＝vsin 30º＝150 km/h

飞机在水平方向和竖直方向的分速度分别是260 km/h和150 km/h。

做一做[2]

如图5.1-8，取一根稍长的细杆，一端固定一根铁钉，另一端用羽毛或纸片做成尾翼，这样就得到了一个能够显示曲线运动速度方向的“飞镖”。在空旷地带把飞镖向斜上方抛出，飞镖在空中的指向就是它做曲线运动的速度方向。飞镖落至地面插入泥土后的指向就是它落地瞬时的速度方向。改变飞镖的投射角，观察它在飞行过程中直到插入地面时的不同角度。

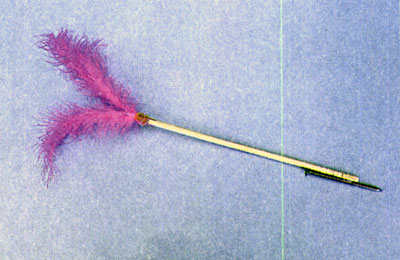
与飞镖在空中做曲线运动的轨迹相联系，体会曲线运动的方向与轨迹曲线的关系。

运动描述的实例

分析下面的实例，对于怎样用物体的位置（位移）和速度描述它在平面中的运动，可以有些更清晰的认识。

演示

在一端封闭、长约1 m的玻璃管内注满清水，水中放一个红蜡做的小圆柱体R。将玻璃管的开口端用橡胶塞塞紧（图5.1-9甲）。

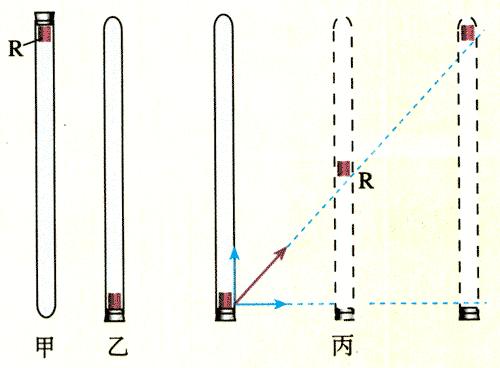
将玻璃管倒置（图乙），蜡块R沿玻璃管上升。如果在玻璃管旁边竖立一个米尺，可以看到，除了开始的一小段外，蜡块上升的速度大致不变。

再次将玻璃管上下颠倒，在上升的同时，将玻璃管紧贴着黑板沿水平方向向右匀速移动（图丙）。以黑板为参照物观察蜡块的运动。

蜡块在做什么样的运动？它在黑板上留下的轨迹是直线吗？也许轨迹是黑板平面内的一条曲线？它的运动是匀速运动吗？也许速度的大小或方向有些变化？这些问题都不是仅凭“看”就能准确回答的。

蜡块的位置

首先，以蜡块开始运动的位置为原点O，水平向右的方向和竖直向上的方向分别为x轴和y轴的方向，建立平面直角坐标系（图5.1-10）。

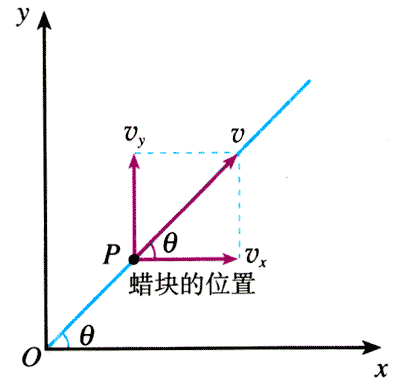
我们设法写出蜡块的坐标随时间变化的关系式。蜡块的x坐标的值等于它与y轴的距离，y坐标的值等于它与x轴的距离。若以v_x表示玻璃管向右移动的速度，以v_y表示蜡块沿玻璃管上升的速度，则有

x＝v_x t

y＝v_y t

请你考虑：怎样计算蜡块对于原点的位移（大小和方向）与时间的关系？

蜡块的速度

速度v与v_x、v_y的关系已经在图5.1-10中标出，因此可以根据勾股定理写出它们之间的关系

v＝\(\sqrt {v_x^2 + v_y^2} \)

根据三角函数的关系，从图5.1-10还可以确定速度v的方向，即角θ的正切

tan θ＝\(\frac{{{v_y}}}{{{v_x}}}\)

蜡块运动的轨迹

蜡块沿着什么样的轨迹运动？在数学上，关于x、y两个变量的关系式描述一条曲线（包括直线），而在上面x、y的表达式中，除了x、y之外还有一个变量t，我们应该从这两个式子中消去t，这样就得到

\[y = \frac{{{v_y}}}{{{v_x}}}x\]

由于v_x和v_y都是常量，所以\(\frac{{{v_y}}}{{{v_x}}}\)也是常量，可见y＝\(\frac{{{v_y}}}{{{v_x}}}\)x代表的是一条过原点的直线，也就是说，蜡块的运动轨迹是直线。

这里说的“常量”，指的是它不随坐标x、y变化。也就是说，在任何位置，的值都是一样的。因此，y＝\(\frac{{{v_y}}}{{{v_x}}}\)x具有正比例函数关系的形式。

物体做曲线运动的条件

物体在什么条件下做曲线运动？观察下面的实验。

演示

一个在水平面上做直线运动的钢球，从侧面给它一个力，例如在钢球运动路线的旁边放一块磁铁，观察钢球的运动。

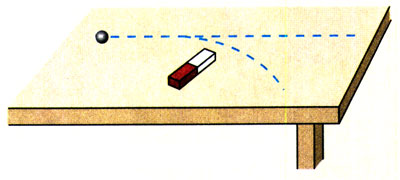
当物体所受合力的方向与它的速度方向不在同一直线上时，物体做曲线运动。

向斜上方抛出的石子，它所受重力的方向与速度的方向不在同一条直线上，它做曲线运动；人造卫星绕地球运行，地球对它的引力与速度方向不在同一条直线上，卫星做曲线运动。

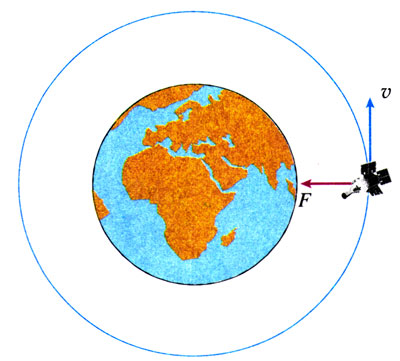
根据牛顿第二定律，物体加速度的方向与它受力的方向总是一致的。当物体受力的方向与它的速度方向不在同一条直线上时，加速度的方向也就与速度方向不一致了，于是物体的速度方向要发生变化，物体就做曲线运动。

本节前面对曲线运动的位移和速度的研究是运动学的内容；而这里关于物体做曲线运动的条件的研究则是动力学的内容。

问题与练习

1．一个质点从平面直角坐标系的原点开始运动并开始计时。它在t₁时刻到达x₁＝2.0 m、y₁＝1.5 m的位置；在t₂时刻到达x₂＝3.6 m、y₂＝4.8 m的位置。作草图表示质点在0～t₁和0～t₂时间内发生的位移l₁和l₂，然后计算它们的大小及它们与x轴的夹角θ₁和θ₂。

2．在许多情况下，跳伞员跳伞后最初一段时间降落伞并不张开，跳伞员做加速运动。随后，降落伞张开，跳伞员做减速运动（图5.1-13）。速度降至一定值后便不再降低，跳伞员以这一速度做匀速运动，直至落地。无风时某跳伞员竖直下落，着地时速度是5 m/s。现在有风，风使他以4 m/s的速度沿水平方向向东运动。他将以多大速度着地？计算并画图说明。

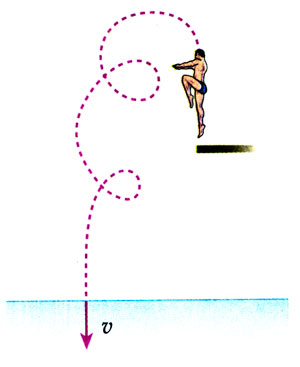
3．跳水运动是一项难度很大又极具观赏性的运动，我国运动员多次在国际跳水赛上摘金夺银，被誉为跳水“梦之队”。图5.1-14是一位跳水运动员高台跳水时头部的运动轨迹，最后运动员沿竖直方向以速度口入水。整个运动过程中，在哪几个位置头部的速度方向与入水时v的方向相同？在哪几个位置与v的方向相反？在图中标出这些位置。

4．汽车以恒定的速率绕圆形广场一周用时2 min，每行驶半周，速度方向改变多少度？汽车每行驶10 s，速度方向改变多少度？先作一个圆表示汽车运动的轨迹，然后作出汽车在相隔10 s的两个位置速度矢量的示意图。

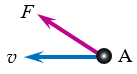
5．一个物体的速度方向如图5.1-15中v所示。从位置A开始，它受到向前但偏右（观察者沿着物体前进的方向看，下同）的合力。到达B时，这个合力的方向突然变得与前进方向相同。达到C时，又突然改为向前但偏左的力。物体最终到达D。请你大致画出物体由A至D的运动轨迹，并标出B点、C点和D点。

发布时间：2016/10/24 下午3:48:47  阅读次数：3079