第四章 B 角速度与线速度的关系

自行车的许多零部件都可做圆周运动，我们将通过对自行车这些零部件运动的研究，进一步学习圆周运动。自行车的发展已有200多年历史，图4-17所示是1885年由意大利制造的用链条传动的自行车，前轮的直径比后轮的大，后经多次改进才发展为今天的自行车。即使在交通工具发达的今天，自行车仍然囚其简单、经济、方便和环保的优点而深受欢迎，它还可用于运动和娱乐，成为全世界各地人们的交通工具和运动器材，图4-18反映人们骑自行车上下班的盛况。你家也有自行车吧？你和你的同学一定非常乐意把自己的自行车作为学习圆周运动的学具。

线速度和角速度既然都反映同一个圆周运动的快慢，两者之间有什么关系？

自主活动

请根据线速度、角速度的定义式以及对弧度的定义，推出线速度和角速度的关系式，并填写下面空格。

（1）当角速度不变时，线速度与半径有____关系，举例说明。

（2）当线速度不变时，角速度与半径有____关系，举例说明。

1．角速度和线速度的关系

v＝rω

实际上，有时用线速度、角速度描述圆周运动的快慢并不方便，测量也比较困难。而转动一周的时间即本章开始所讲的周期，以及单位时间绕圆周的圈数则更容易观察和测量。因此，除了线速度、角速度之外，还可以用周期和转速来描述圆周运动的快慢。

自主活动

请根据各物理量的定义推导出：

（1）周期与线速度的关系式。

（2）周期与角速度的关系式。

用以上“自主活动”中的推导方法还可得出转速与周期、线速度、角速度的关系式。

2．周期

质点做匀速圆周运动时，沿着圆周运动一周所用的时间叫做匀速圆周运动的周期，用符号T表示。

周期与绕速度、角速度的关系

T＝$\frac{2\pi }{\omega }$

T＝$\frac{2\pi r}{v}$

3．转速（rotational speed）

质点做匀速圆周运动时每秒转动的圈数，就叫做匀速圆周运动的转速，用符号n表示。

转速的单位是r/s（读作转每秒）。

在技术上常以每分的转动圈数r/min故单位（读作转每分），

1r/s＝60r/min。

如果以r/s为转速单位，则转速与线速度、角速度、周期的关系

n＝$\frac{v}{2\pi r}$

n＝$\frac{\omega }{2\pi }$

n＝$\frac{1}{T}$

示例1

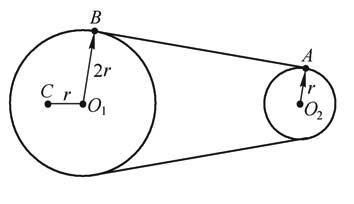
如图4-19所示，两个皮带轮的转轴分别是O₁和O₂，设转动时皮带不打滑，则皮带轮上A、B、C三点运动快慢的正确关系是（  ）。

（A）v_A＝v_B，v_B＞v_C

（B）ω_A＝ω_B，v_B＞v_C

（C）v_A＝v_B，ω_B＝ω_C

分析：A、B两点的线速度大小都等于皮带的运行速度，所以v_A＝v_B，B、C两点在同一个物体上，角速度相等，所以ω_B＝ω_C。O₁C＜O₁B，它们角速度相等，所v_B＞v_C，正确答案（A）和（C）。

解答：（A）、（C）。

示例2

机器上的转盘匀速转动，每分转45圈，离转轴0.1m处有一个小螺母，求小螺母做圆周运动的周期、角速度、线速度。

【分析】周期、角速度、线速度和转速都反映圆周运动的快慢，它们有一定的关系，知道周期、角速度和转速三个物理量中的任何一个，就可以求出其他两个物理量。如果还知道半径，就可以求出线速度。

【解答】由匀速圆周运动的周期和转速的关系可求周期

T＝$\frac{1}{n}$＝$\frac{60}{45}$s＝$\frac{4}{3}$s。

由匀速圆周运动的周期和角速度的关系可求角速度

ω＝$\frac{2\pi }{T}$＝$\frac{3\pi }{2}$rad/s≈4.71rad/s。

由线速度和角速度的关系可求线速度

v＝ωr＝0.1×4.71m/s＝0.471m/s。

点击

物体的转动

当我们研究一个物体绕固定轴的转动时，该物体不能作为一个质点，我们也不能说这个物体在做圆周运动，因为物体的定轴转动和质点的圆周运动是不同的运动。但是当物体绕固定轴转动时，物体上除轴线外的各点都在做圆周运动，而且各点的角速度、周期和转速都相等。但各点的线速度大小不一定相等，只有到圆心距离相等的各点的线速度大小才相等。在同一个转动物体上，各点线速度大小与其到轴线的距离成正比。

STS

磁（光）盘的线速度和角速度

计算机都有磁盘驱动器（图4-20）和光盘驱动器，磁（光）盘驱动器在工作时，应保持磁（光）盘的角速度不变，还是保持读取信息的磁（激光）头处的线速度不变？相信你看完以下短文后就会找到答案。

由于磁（光）盘是以等密度方式存储数据的，因此早期的驱动器在读磁（光）盘的时候，都是采用恒定线速度的方式。它通过改变主轴电机的角迷度，使磁（激光）头从盘的内圈移动到外圈的过程中，单位时间内读过的轨道弧线长度相等。

这样势必要求读取内外圈时带动磁（光）盘的电机角速度不一样。当驱动器的速度比较高以后，频繁改变主轴的角速度，将降低驱动器电机的寿命。因此，恒定线速度技术只适合于低速的驱动器。对于高速驱动器，则用另一种方式，即保持恒定角速度的方式，在这种方式下主轴电机的转速不变。因此，在读取内圈和外圈的数据时线速度会有差异，读取信息的速度也会不同。最新的技术则是区域恒定角速度技术，即在读内圈数据时，以恒定线速度的方式读取，而在读外圈数据时，以恒定角速度的方式读取。这样既节约成本，也提高了性能，目前市面上的大部分高速驱动器都是采用这种方式。

我们已经学习了关于圆周运动的知识，如何运用学过的知识来认识和研究实际的圆周运动呢？下面我们以常见的自行车为对象开展课题研究。

探索研究

自行车中的圆周运动

【课题】

探究自行车中的圆周运动

【背景知识】

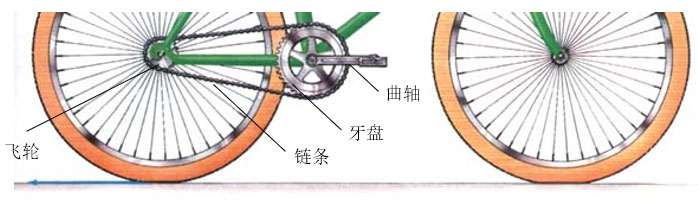
图4-21所示是自行车最主要的传动部件，牙盘（大齿轮）和飞轮（小齿轮）用链条相连，踏脚曲柄和牙盘固定连接，后车轮与飞轮固定连接，当用力踏踏脚板时，后车轮就会转动，从而使自行车前进。自行车前进时，车轮在地面每滚动一圈，车身就前进等于车轮周长的距离，轮缘上的点既随车身向前移动，又同时绕轮轴做圆周运动。

【任务】

1．探究自行车各转动部件的传动关系。

2．测算该辆自行车的踏脚板转动一周，自行车前进的距离。

【参考步骤】

1．观察自行车中有哪些零件做圆周运动，搞清各主要零件的传动关系。

2．猜测该辆自行车的踏脚板转动一周，自行车可前进的距离。

3．确定所用的计算公式。

4．确定需要测量的物理量。

5．确定需要的测量工具。

6．进行人员分工。

7．测量、记录、计算。

8．比较测算的结果与猜测的差别，进行分析评价。

【记录建议】

可记录你事先猜测的距离、所用的计算公式、需要测量的量、所用的测量工具、人员分工、原始数据、结论等。

【结论】

______________________________________________________________________。

【自评意见】

_______________________________________________________________________。

【教师评价】

______________________________________________________________________。

说明：每位同学可根据实际情况分工完成其中一个任务，也可共同确立其他课题，研究圆周运动。

发布时间：2016/3/22 上午11:44:02  阅读次数：6949