三、单摆

单摆的振动特点  我们已经知道，在一根细线下端拴一个小球就做成了一个单摆。但是这不是单摆的严格说法。在物理学里，单摆是实际的摆（例如钟摆）的理想化，是指在一根不能伸长、又没有质量的线的下端系一质点。利用这个理想化的模型，将使定量研究摆的运动大大简化。

当单摆静止不动时，摆线竖直下垂，摆锤m（质点）受的重力G＝mg跟摆线对它的拉力T互相平衡。

使摆锤偏离平衡位置，然后放开，摆锤就在重力G和拉力T的作用下，沿着以平衡位置O为中点的一段圆弧左右振动。我们来分析摆锤运动到任意一点P时的受力情况（图9-3）。这时摆线与竖直方向的夹角是α，重力G沿摆线方向的分力Fʹ跟拉力T的合力，沿着摆线指向圆心（悬挂点），是使摆锤沿圆弧运动的向心力，它只改变摆锤运动的方向，不改变运动的快慢。因此，在研究摆锤沿圆弧运动的位置变化时，不需要考虑向心力，而只考虑重力沿圆弧切线方向的分力F，因为正是这个分力F是使摆锤振动的回复力。

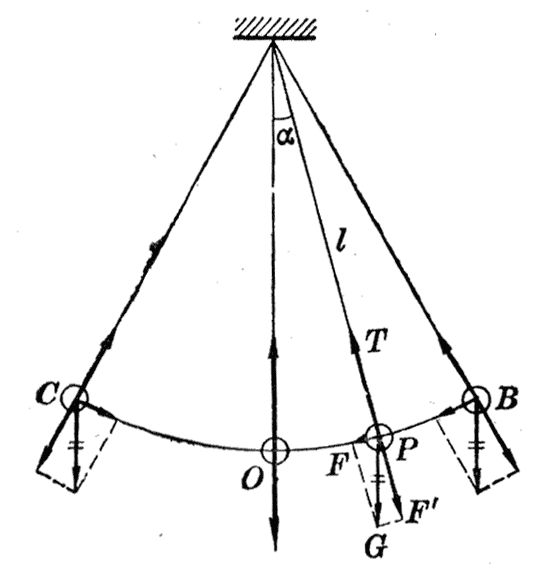
重力G＝mg沿圆弧切线的分力F＝mgsinα。当α很小时（5°以下），圆弧可以近似地看成直线，分力F可以近似地看作沿这条直线作用，OP就是摆锤偏离平衡位置的位移x。设摆长是l，因为sinα≈\(\frac{x}{l}\)，所以

\[F = - \frac{{mg}}{l}x\]

式中负号表示力F跟位移x的方向相反，由于m、g、l都有一定的数值，mg可以用一个常数k来代替，所以上式可以写成

F＝－kx。

可见，在摆角很小的情况下，单摆振动时回复力跟位移成正比而方向相反，是做简谐振动。

单摆的周期公式  将k＝代入简谐振动的周期公式，可以得到

\[T = 2\pi \sqrt {\frac{l}{g}} \]

这就是单摆的周期公式，它表明在摆角很小的情况下（根据周期公式算出的T值与实际测定值间的误差，随摆角增大而增大。摆角为7°时，误差为0.1%；15°时，0.5%；23°时，1%。单摆最大摆角一般应小于5°。），单摆的周期跟摆长的平方根成正比，跟重力加速度的平方根成反比，而跟摆锤的质量、振幅无关。

在一定的地点，g的值一定，一定摆长的单摆就有恒定不变的周期。摆的这个性质被利用在摆钟上计量时间。相反，如果测出摆长l和周期T，也可以利用单摆的周期公式确定g的值，由于单摆的摆长l和周期T都容易测量，所以利用单摆可以很方便地测定重力加速度g的值，不象利用自由落体运动测g那样麻烦。

练习三

（1）假如把单摆和弹簧振子都从地球移到月球上，它们的振动频率是否改变？为什么？

（2）两个单摆，它们的摆长的比是1∶4，求它们的周期的比。两个单摆，它们的频率的比是1∶4，求它们的摆长的比。

（3）测某地的重力加速度时，用了一个摆长为2m的单摆，测得100次全振动所用的时间是4分44秒。这个地方的重力加速度多大？

（4）假如把上题中的单摆拿到月球上去，月球的重力加速度是1.6m/s²，摆的周期将变为多少秒？ 

发布时间：2015/8/13 下午7:22:20  阅读次数：3161