第一讲B 平抛运动

在学习本节之前，建议同学们到学校运动场去做一个实验：当你匀速向前奔跑时，放开高举在手中的网球，让它自由落下，看看该球将会落在何处。

类似的问题如图1-5所示：从一艘正在匀速行驶的帆船的桅杆上落下一块石块，这石块将怎样运动？早在17世纪前就有不少学者对这个问题做了思考，伽利略利用它的惯性原理终于想通了这个问题，对于站立在岸上的观察者来说，在帆船停靠在岸边和匀速行驶的两种情况下，石块的运动是不同的。当帆船停靠在岸边时，站立在岸上的人看到石块做自由落体运动；当帆船匀速行驶时，这石块不仅在竖直方向做自由落体运动，而且由于惯性，它同时还要沿水平方向做匀速运动，因此它的运动路径应当如图1-5中的虚线所示。

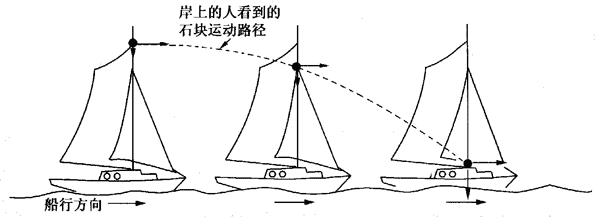
以一定速度将物体抛出，在空气阻力可以忽略的情况下物体所做的运动叫做抛体运动。如果抛出物体的初速度沿水平方向，该物体的运动便叫做平抛运动，以一定速度滑过水平桌面落下的物体、运动员水平击出的排球或棒球、水平管子中喷出的水流等，都可近似看作平抛运动。

一、平抛运动的规律

平抛运动有怎样的特点？它的轨迹如何？

图1-6（a）是一个能够显示平抛运动及其特点的演示实验。用小锤敲击弹性金属片，小球A就沿水平方向飞出，做平抛运动；同时小球B被松开，做自由落体运动。敲击弹性金属片的力愈大，A球的水平初速度就愈大，它飞出的水平距离就愈远，但从实验大致可以看出，无论A球的初速度多大，它总是与B球同时落地。此外，还可改变小球离地面的高度，重复做这个实验。图1- 6（b）是该装置一次实验的频闪摄影照片，同时显示了A、B球分别做平抛运动和自由落体运动的轨迹。

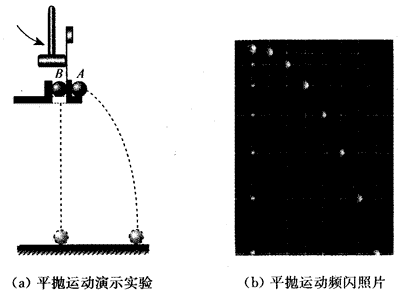
为了认识和把握平抛运动，需要知道平抛运动的规律。但从演示实验中可以看出，平抛运动是一种曲线运动，它的速度和位移不仅大小随时间变化，而且方向也随时间变化，比较复杂。

那么，能否利用运动的合成和分解方法来认识平抛运动的规律，解决平抛运动的问题呢？

回答是肯定的。实际上，平抛运动取决于两个因素：水平方向的初速度v₀和竖直方向由于受到重力作用而产生的重力加速度g。因此，按照运动的合成与分解方法，可将平抛运动看成是水平方向的匀速直线运动（即惯性运动）和竖直方向自由落体运动这两个分运动的合运动。

注意：惯性是阐明抛体运动的关键。当抛出的物体由于重力加速度而在竖直方向做自由落体运动时，它在水平方向同时以v₀的初速度做惯性运动。这两个分运动互不干扰，彼此独立存在，每个分运动表现出好像另一个分运动不存在一样。

通过上述分析，我们现在可以建立描写平抛运动规律的公式了，取水平方向为x轴，正方向与初速度v₀的方向相同；竖直方向为y轴，正方向向下；抛出点为坐标原点O。这样，平抛运动的规律就可用它的两个分运动的基本公式（包括速度公式和位移公式）的简单组合表示：

v_x＝v₀，v_y＝gt；

x＝v₀t，y＝$\frac{1}{2}$gt²；

自主活动

如图1-7所示，小球在A点开始做平抛运动，已知抛出后经过2s抵达图中的P点，试在图中标出抛出后经过1s和3s时小球的位置。

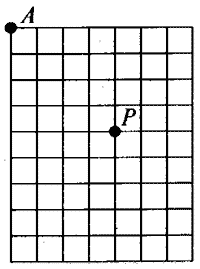
【示例1】平抛运动物体的水平初速度v₀＝10m/s，求它在0s、1s、2s、3s、4s、……时刻的位置，画出它的轨迹。（g＝10m/s²）

【分析】利用平抛运动的位移公式x＝v₀t，y＝$\frac{1}{2}$gt²，已知初速度v₀，便可求出任一时刻物体位移的水平分量x和竖直分量y，然后在xOy坐标系中用描点法将题中各时刻的位置表示出来，并用光滑的曲线将这些点连接起来，便得到平抛物体的运动轨迹。

【解答】由平抛运动的位移公式x＝v₀t和y＝$\frac{1}{2}$gt²得到的各相应时刻的位置显示在下表中。

将上表中各时刻物体的位置标记在xOy坐标系中，然后用光滑的曲线将这些位置点连接起来，就得到如图1-8所示的平抛物体的运动轨迹。

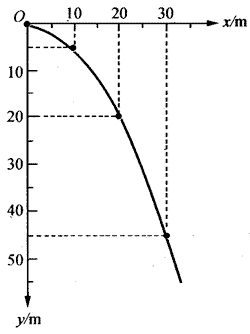
【讨论】由两个分运动的位移公式联立消去t，可得到平抛运动物体的竖直方向位移y和水平方向位移x的关系式：y＝$\frac{g}{2v_0^2}$x²，图1-8就是这个轨迹方程的图象表示。在平抛运动物体的轨迹方程中，g、v₀都是与x和y无关的常量。因此，这样的轨迹方程正是初中数学中学过的抛物线方程y＝ax²。实际上，这也是将二次幂函数的图象叫做“抛物线”的原因。

自主活动

在图1-8中，画出t＝1s，2s，3s时刻平抛物体的速度矢量和位移矢量。

二、平抛运动物体的飞行时间和射程

平抛运动是一种曲线运动，较为复杂，而它的两个分运动是较为简单的直线运动。利用运动的合成与分解方法，我们可用两个简单的直线分运动来描述平抛运动。因此，平抛运动的特征也可通过分运动的特征加以认识和掌握。

抛体落地前飞行的水平距离称为射程。

那么，怎样确定平抛运动物体的飞行时间和射程呢？

1．平抛运动物体的飞行时间

平抛运动物体的飞行时间由竖直方向分运动的规律确定，因为水平方向分运动是惯性运动，如果没有竖直方向的重力将它拉向地面，则该平抛运动物体将保持同样的高度沿水平方向一直飞行下去。

由竖直分运动的位移公式y＝$\frac{1}{2}$gt²可知，平抛运动物体的飞行时间为

$$t=\sqrt{\frac{2y}{g}}$$

可见，平抛运动物体的飞行时间仅与抛出时物体的高度y有关，而与初速度v₀无关，在相同高度上做平抛运动的物体无论其水平初速度多大（包括v₀＝0），无论落地点的水平距离x多大，它们的飞行时间都是相同的。

大家谈

物体抛出时的水平初速度无论多大，它的飞行时间会是相同的吗？

2．平抛运动物体的射程

在平抛运动中，物体飞行的水平距离可由水平分运动的位移公式x＝v₀t推出，但其中的飞行时间t则由竖直方向分运动的规律确定，将上述飞行时间的结果代入，可得

$$x=v_0\sqrt{\frac{2y}{g}}$$

可见，平抛运动物体的射程取决于抛出时的高度y与水平初速度v₀。当高度y一定时，平抛运动物体飞行的水平距离x与它的初速度v₀成正比。这也是平抛运动物体在水平方向上以速度v₀做惯性运动的结果。

3．平抛运动物体的速度

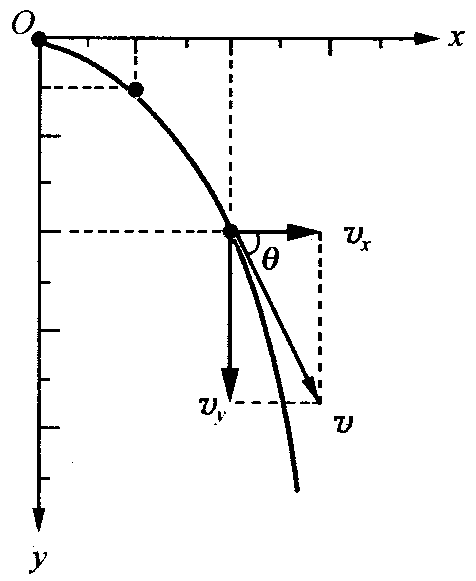
平抛运动物体任一时刻的速度v是它的两个分运动速度v_x＝v₀、v_y＝gt的矢量和，如图1-9所示。根据平行四边形定则，其合速度的大小是

$$v=\sqrt{v_x^2+v_y^2}=\sqrt{v_0^2+{(gt)}^2}=\sqrt{v_0^2+2gy}$$

速度的方向则可用它与x轴的夹角θ表示，即

$$\tan \theta =\frac{v_y}{v_x}=\frac{gt}{v_0}=\frac{\sqrt{2gy}}{v_0}$$

自主活动

试用机械能守恒定律导出平抛运动物体的速度与下落高度的关系式。

【示例2】水平飞行的轰炸机在0.90km高度上空投弹，如图1-10所示，试问：

（1）为击中预定目标，应当在离该目标的水平距离多远处投弹？

（2）炸弹落地时速度的大小和方向如何？不计空气阻力，取g＝10m/s²，设轰炸机水平飞行的速度为3.6×10²km/h。

【分析】在运动的合成和分解问题中，合运动与分运动发生在同一时间内。我们可先算出竖直方向分运动（自由落体运动）的时间，这也就是炸弹的实际平抛运动的飞行时间，在这段时间内，如果炸弹在水平方向上通过的距离等于飞机投弹时离开目标的水平距离（如图1-10中所示），就能命中目标。

【解答】（1）求水平距离。

利用竖直方向分运动的规律y＝$\frac{1}{2}$gt²可知，炸弹的飞行时间为t＝$\sqrt{\frac{2y}{g}}$。再利用水平方向分运动的规律可知，在这段时间内，炸弹飞行的水平距离为

$$x=v_{0}t=v_0\sqrt{\frac{2y}{g}}$$

代入已知数据：v₀＝3.6×10²km/h＝100m/s，y＝900m，g＝10m/s²，可得

x＝100×$\sqrt{\frac{2\times 900}{10}}$m＝1341.6m。

因此这架飞机应当在距离目标的水平距离为1341.6m处投下炸弹，才能击中该目标。

（2）求炸弹落地时的速度。

炸弹落地时速度的水平分量和竖直分量分别为v_x＝v₀和v_y＝gt＝$\sqrt{2gy}$，因此它的大小为

$$v=\sqrt{v_x^2+v_y^2}=\sqrt{v_0^2+2gy}$$

代入数据，得

v＝$\sqrt{{100}^2+2\times 10\times 900}$m/s＝167.3m/s。

速度的方向与x轴夹角θ的正切为

$$\tan \theta =\frac{v_y}{v_x}=\frac{\sqrt{2gy}}{v_0}$$

代入数据，得

tanθ＝$\frac{\sqrt{2\times 10\times 900}}{100}$＝1.34，

故θ＝53.3°。

因此炸弹落地时速度的大小为167.3m/s，速度的方向与地面的夹角θ为53.3°。

此例分析，我们忽略了空气阻力的作用。实际情形，由于空气阻力的作用，炸弹落地的速度和方向会有较大的偏差。

大家谈

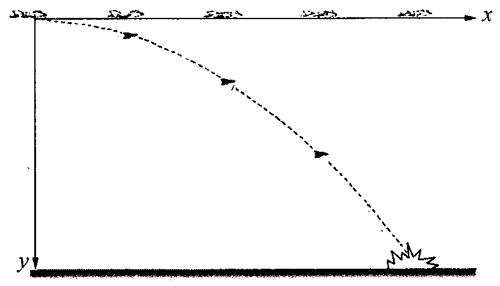
站在地面上的人看到从正在做水平飞行的飞机上投下一系列炸弹的情景是否如图1-11所示？飞机驾驶员看到的又是怎样的情景？

三、［学生实验］描绘平抛运动的轨迹

实验目的

（1）利用有连拍功能的数码相机或摄像机获得平抛运动的轨迹；

（2）利用DIS实验研究平抛物体的飞行时间t和下落高度h、初速度v₀之间的关系；平抛物体的射程x与v₀、t之间的关系。

实验器材

有连拍功能的数码相机或摄像机，以及由斜面滑槽和支架、金属小球、光电门传感器、碰撞传感器等组成的DIS平抛运动实验装置。

实验步骤

实验装置如图1-12所示。

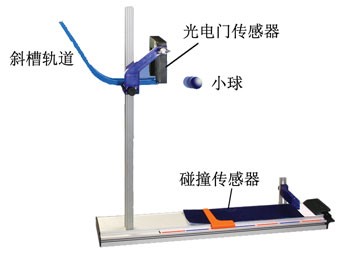
（1）控制斜槽导轨的水平槽口高度，让小球从斜槽的不同高度斜槽导轨处滚下，以4种不同的速度冲出水平槽口在空中做平抛运动。利用安置在槽口的光电门传感器测量小球平抛运动的初速度v₀，利用安置在底板上的碰撞传感器测量小球的飞行时间t并显示在计算机屏幕上。落地点的水平距离x由底座上的标尺读出。将这些数据记录在预先设计好的表格中。

（2）改变斜槽水平槽口的高度，重复步骤（1）中的实验，将显示在计算机屏幕上的这些数据记录在预先设计好的第二张表格中。

（3）用数码相机的连拍功能（或摄像机），在上述两组实验中，各选一次实验，拍摄小球做平抛运动的过程，将所摄得的一组照片输入计算机中，然后进行处理，并将这些照片图像叠合在一起以获得小球做平抛运动的轨迹。

分析数据，得出结论

（1）根据表中物体抛出时的高度h和初速度v₀的数据，分别计算出射程和飞行时间的理论值，然后与相应的实验数据进行比较，进行分析，得出结论。

（2）考察由数码相机所得到的小球做平抛运动的轨迹图象，分析由此得到的某些信息，如水平分速度、竖直分速度等。

发布时间：2015/6/26 上午10:00:36  阅读次数：3256