第一讲A 运动的合成与分解

在基础型物理课程中已学过“力的合成与分解”。类似地，运动（包括速度和位移等）也可以合成和分解。运动的合成与分解是科学分析和综合方法在物理学中的具体应用，这种方法为我们研究较复杂的运动提供了可能。例如，抛体运动通常是一种曲线运动，我们可利用运动的合成与分解方法将它分解为两个互相垂直的直线运动（如匀速直线运动和匀变速直线运动）。于是，较复杂的抛体运动的特征和基本规律就可通过简单的直线运动的特征和规律的综合进行描述。

直升机现已广泛应用于突发性灾难的救援工作。2006年8月18日上海《新闻晨报》的一篇关于洋山港海域搜救演练的报道说：“昨天上午10时50分左右，‘东海’号货轮突然爆炸起火，船体倾斜进水，船上一名船员重伤，四名船员落水，情况危急！以这样的惊险一幕，拉开了我国东部海区海空立体搜救演练的序幕……”图1-1显示了救助直升机正在将“伤员”转移到救助船上的情景。为了达到最快速的救援效果，直升机常常一边收拢缆绳，提升被救者，将伤员接进机舱；一边随即沿着水平方向飞向救助船或岸边。

从运动学上说，在图1-1所示的情景中，被救者同时参加了两种运动：随飞机沿水平方向的运动和沿竖直方向向上的运动。这两种运动（可叫做分运动）的综合效果则显示为被救者沿着斜上方向的运动（可叫做合运动）。这里，我们遇到了互成角度的运动的合成和分解问题。

一、同一直线上运动的合成与分解

我们先来讨论一种最简单的情况，即同一方向上运动的合成与分解问题。

在拓展型课程Ⅰ第一册第一讲的学习中我们已经知道，初速为v₀的匀变速直线运动的规律，可由它的速度v和位移s随时间t变化的两个公式描述：

v＝v₀＋at；s＝v₀t＋$\frac{1}{2}$at²，

其中a为加速度。

从上述初速为v₀的匀变速直线运动的基本公式中能否获得某些新的见解？

上两式等号右边都包括两项，第一项表示物体做匀速运动时它的速度和位移随时间变化的规律；第二项表示物体做初速为零的匀变速直线运动时它的速度和位移随时间变化的规律。现在我们将上述速度公式和位移公式记为

v＝v₁＋v₂；s＝s₁＋s₂，

其中：

v₁＝v₀，v₂＝at；

s₁＝v₀t，s₂＝$\frac{1}{2}$at²

从数学上说，上述表示并无新意，但从物理上说，这样的表示包含了一种新的观念：初速不为零的匀变速直线运动可分解为同一直线上的两种最为简单的分运动——速度为v₀的匀速直线运动和初速为零、加速度为a的匀变速直线运动，于是，初速不为零的匀变速直线运动可视为同一直线上的匀速直线运动和初速为零的匀变速直线运动这两种分运动的合运动。v、s可分别称为合速度和合位移；v₁、v₂和s₁、s₂可分别称为分速度和分位移。由分运动求合运动的过程叫做运动的合成；由合运动求分运动的过程叫做运动的分解。

大家谈

怎样根据运动合成与分解的观念处理竖直上抛运动，并由此写出竖直上抛运动的基本公式？

【示例1】购物中心的自动电梯在10 s内可把静立在电梯上的顾客送上楼；如果电梯不动，顾客自己走上去：需要30 s。问顾客随着开行的电梯走上去需多少时间？

【分析】为了求出时间，可先算出顾客随着开行的电梯走上去时的速度v。从地面上看，顾客随着开行的电梯走上去的速度包括两部分：电梯开行的速度v₁和顾客在电梯上行走的速度v₂。因此v可看成是v₁和v₂这两个速度的合速度。

【解答】设电梯的长度为L，则电梯运行的速度为

v₁＝$\frac{L}{10}$；

顾客在电梯上行走的速度为

v₂＝$\frac{L}{30}$；

因此，顾客沿着开行电梯走上去的速度为

v＝v₁＋v₂＝$\frac{4L}{30}$，

所需时间为

t＝$\frac{L}{v}$＝$\frac{30}{4}$s＝7.5s。

【讨论】在时间t内，电梯行走的距离为s₁＝v₁t＝$\frac{3}{4}$L，顾客沿着电梯行走的距离为s₂＝v₂t＝$\frac{1}{4}$L。在时间t内顾客一边在电梯上行走，一边又随电梯移动，因此顾客移动的合距离为s＝s₁＋s₂。代入上面的结果，得s＝L。这正是我们所期望的。

二、沿不同方向运动的合成与分解

同一方向上运动的合成和分解问题比较简单，合运动与分运动的速度和位移的关系可用简单的代数和（或差）表示。

在一般实际问题中，分运动可能在不同方向上。此时应当用什么方法处理运动的合成与分解的问题呢？

自主活动

如图1-2所示，在一张白纸上取一点为O。若让铅笔（或圆珠笔）自O点沿着一根横向直尺匀速移动，便画出一根水平直线；若让笔尖在O点处靠在尺上不动，推尺匀速上升，便画出一根竖直向上的直线；若让笔尖自O点沿着横向直尺匀速移动的同时，让尺竖直向上匀速平移，看看你所画出的笔尖的运动图像。

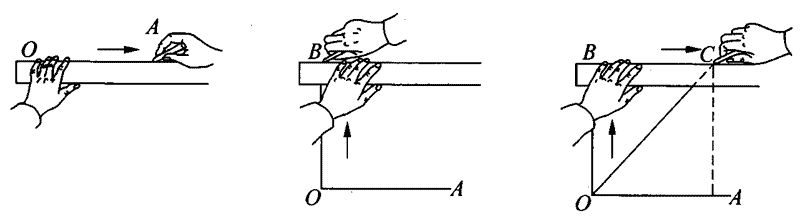
在自主活动中，如图1-2所示，当笔尖同时沿水平方向和竖直方向做匀速直线运动时，它的合运动轨迹是一条斜向上的直线。为了描写笔尖的合运动规律，我们建立如图1-3所示的直角坐标系：运动开始时笔尖的位置为原点，水平向右的方向和竖直向上的方向分别为x轴和y轴的正方向。笔尖沿直尺向右的速度设为v₁，直尺向上的平移速度设为v₂，于是，笔尖的合运动规律可用沿x轴方向和沿y轴方向的两个分运动的基本公式表示：

v_x＝v₁，v_y＝v₂

x＝v_xt，y＝v_yt

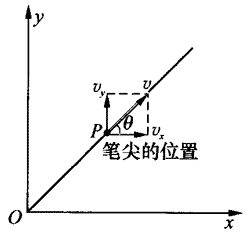
从上面的讨论可以看出，如果分运动不在同一直线上，便要利用“平行四边形定则”进行运动的合成或分解。如图1-3中所示，由同一起点作出表示两个分运动的速度或位移矢量的线段，以它们为邻边作一平行四边形，由起点所作的对角线即表示合运动的速度或位移矢量，在正交坐标系中对运动进行合成或分解比较简单些，此时的平行四边形变成了矩形，合运动的位移和速度与x轴和y轴方向上分运动的位移和速度之间的关系可运用直角三角形知识得到。

点击

运动的合成和分解就是指运动物体的速度和位移的合成和分解。在基础型物理课程中，我们曾经学习了反映合力和分力关系的平行四边形定则，现在又介绍了合速度与分速度、合位移与分位移的平行四边形定则，凡是研究有方向性的物理量（矢量）的合成和分解问题，就要利用平行四边形定则。

三、合运动与分运动的位移和速度

仍然以上页自主活动中笔尖的运动为例，来考察物体的合运动与分运动的关系。

1．合运动的位移

如图1-3所示，笔尖的位移可用它的分运动表示，也可用它的合运动表示。从计时开始到时刻t，笔尖沿x轴和y轴方向的两个分位移分别是x＝v_xt和y＝v_yt。而从计时开始到时刻t，笔尖的合位移是s＝$\sqrt{x^2+y^2}$＝$\sqrt{{(v_{x}t)}^2+{(v_{y}t)}^2}$。因此有

s＝$\sqrt{x^2+y^2}$＝$\sqrt{v_x^2+v_y^2}$t

2．合运动的轨迹

笔尖运动的轨迹是什么？包含x、y两个变量的方程代表xOy平面上的一条曲线（包括直线）。从上面的x和y的表达式中消去t，便可得到笔尖运动的轨迹方程：

$$y=\frac{v_y}{v_x}x$$

由于现在v_y和v_x都是常量，所以上式所代表的是一条过原点的直线，也就是说，笔尖在纸面上的合运动的轨迹是一条直线，如图1-3所示。

3．合运动的速度

在笔尖合位移大小的表式s＝$\sqrt{v_x^2+v_y^2}$t中，因子$\sqrt{v_x^2+v_y^2}$现在是一个常量，这个常量与时间的乘积等于合位移的大小，所以它表示笔尖在纸面上移动的合速度v，即

v＝$\sqrt{v_x^2+v_y^2}$

速度和位移都是矢量，不仅有大小，还有方向。笔尖合运动速度的方向可用它与x轴的夹角θ表示，其值可通过下式得到：

tanθ＝$\frac{v_y}{v_x}$。

合位移的方向也可用图1-3中的θ角表示。在现在的情况下，笔尖的合运动是直线运动，所以它的合速度和合位移的方向相同。在下节中将会看到，在一般情况下如果合运动是曲线运动，其速度和位移的方向要随时间而改变，且两者的方向一般也不相同。

【示例2】某直升机在将下端缚有被洪水围困者的缆绳收进机舱的过程中，以10m/s的恒定速度沿斜上方向飞行，其速度方向与水平方向成30°角。

（1）求直升机水平方向分速度和竖直方向分速度；

（2）经10 s，该机上升的高度是多少？水平方向飞行了多少距离？

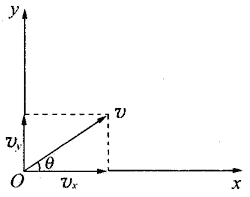
【分析】飞机斜向上飞的运动可分解为水平方向和竖直方向两个分运动。在图1-4所示的坐标系中，将直升机的速度v分解为水平分速度v_x和竖直分速度v_y。知道了分速度，便可算出分位移，即时间t内该机上升的高度和飞行的水平距离。

【解答】（1）该机的水平分速度和竖直分速度分别是

v_x＝vcosθ＝10×cos30°m/s＝8.66m/s，

v_y＝vsinθ＝10×sin30°m/s＝5m/s

（2）经10s直升机上升的离度是

y＝v_yt＝vsinθ·t＝10×sin30°×10m＝50m

经10s直升机飞行的水平距离是

x＝v_xt＝vcosθ·t＝10×cos30°×10m＝86.6m

【讨论】本例结果表明，如果合运动是匀速直线运动，则任意两个方向上的分运动也都是匀速直线运动，反之亦然。那么如果在一个方向上的分运动是匀速直线运动，而另一个方向上的分运动是匀加速直线运动，它们的合运动又如何呢？

发布时间：2015/6/26 上午9:17:33  阅读次数：2779